Taxonomy of Benchmarks in Graph Representation Learning

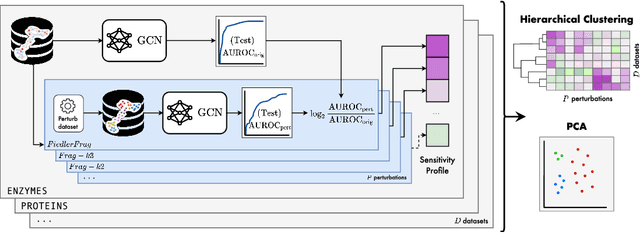
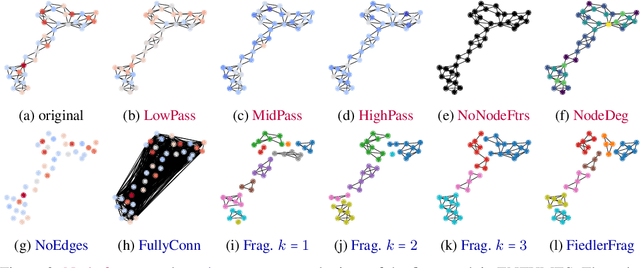
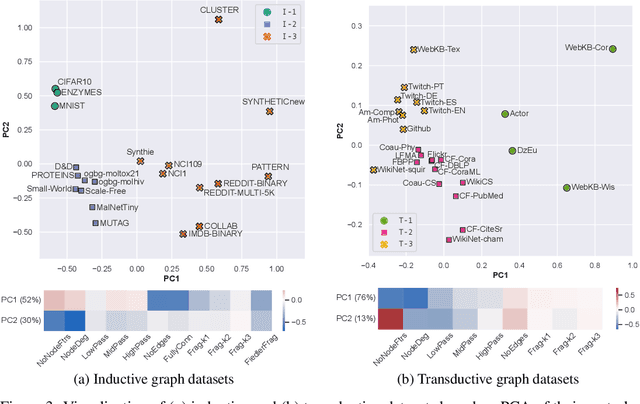
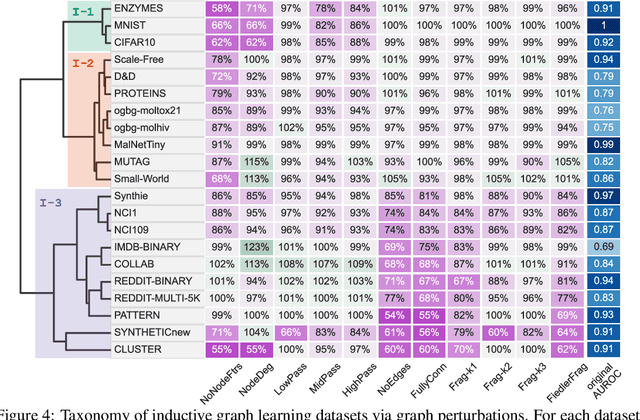
Graph Neural Networks (GNNs) extend the success of neural networks to graph-structured data by accounting for their intrinsic geometry. While extensive research has been done on developing GNN models with superior performance according to a collection of graph representation learning benchmarks, it is currently not well understood what aspects of a given model are probed by them. For example, to what extent do they test the ability of a model to leverage graph structure vs. node features? Here, we develop a principled approach to taxonomize benchmarking datasets according to a $\textit{sensitivity profile}$ that is based on how much GNN performance changes due to a collection of graph perturbations. Our data-driven analysis provides a deeper understanding of which benchmarking data characteristics are leveraged by GNNs. Consequently, our taxonomy can aid in selection and development of adequate graph benchmarks, and better informed evaluation of future GNN methods. Finally, our approach and implementation in $\texttt{GTaxoGym}$ package are extendable to multiple graph prediction task types and future datasets.

Structure-Aware Transformer for Graph Representation Learning

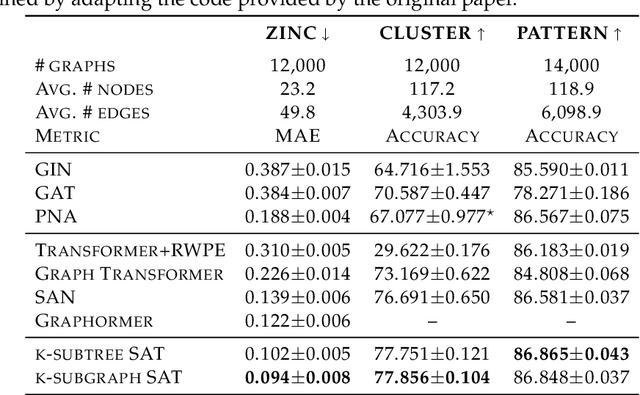
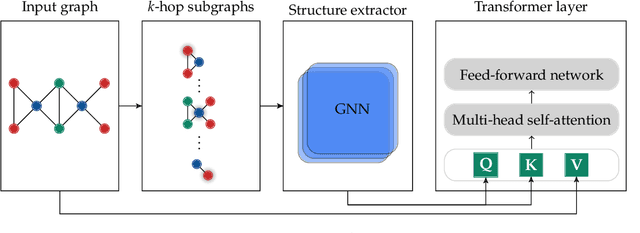
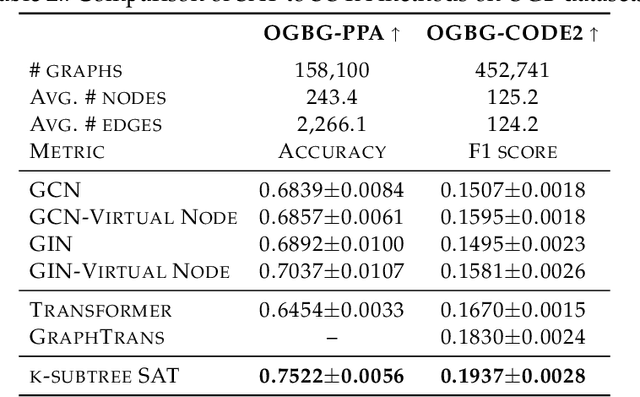
The Transformer architecture has gained growing attention in graph representation learning recently, as it naturally overcomes several limitations of graph neural networks (GNNs) by avoiding their strict structural inductive biases and instead only encoding the graph structure via positional encoding. Here, we show that the node representations generated by the Transformer with positional encoding do not necessarily capture structural similarity between them. To address this issue, we propose the Structure-Aware Transformer, a class of simple and flexible graph transformers built upon a new self-attention mechanism. This new self-attention incorporates structural information into the original self-attention by extracting a subgraph representation rooted at each node before computing the attention. We propose several methods for automatically generating the subgraph representation and show theoretically that the resulting representations are at least as expressive as the subgraph representations. Empirically, our method achieves state-of-the-art performance on five graph prediction benchmarks. Our structure-aware framework can leverage any existing GNN to extract the subgraph representation, and we show that it systematically improves performance relative to the base GNN model, successfully combining the advantages of GNNs and transformers.

The magnitude vector of images

The magnitude of a finite metric space is a recently-introduced invariant quantity. Despite beneficial theoretical and practical properties, such as a general utility for outlier detection, and a close connection to Laplace radial basis kernels, magnitude has received little attention by the machine learning community so far. In this work, we investigate the properties of magnitude on individual images, with each image forming its own metric space. We show that the known properties of outlier detection translate to edge detection in images and we give supporting theoretical justifications. In addition, we provide a proof of concept of its utility by using a novel magnitude layer to defend against adversarial attacks. Since naive magnitude calculations may be computationally prohibitive, we introduce an algorithm that leverages the regular structure of images to dramatically reduce the computational cost.

Towards a Taxonomy of Graph Learning Datasets

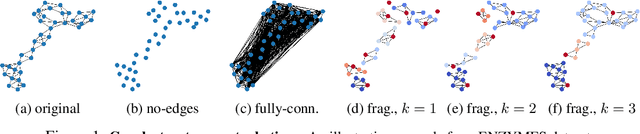
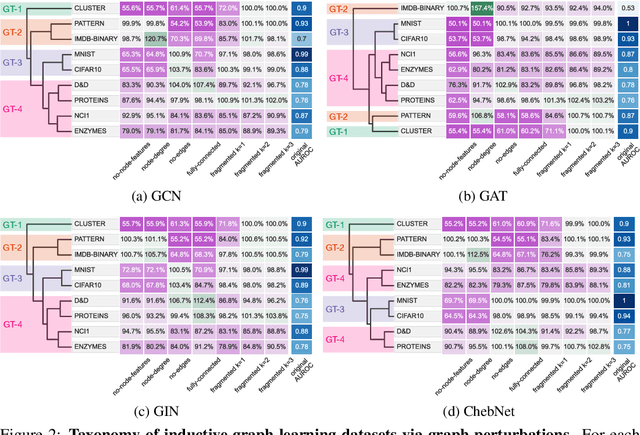
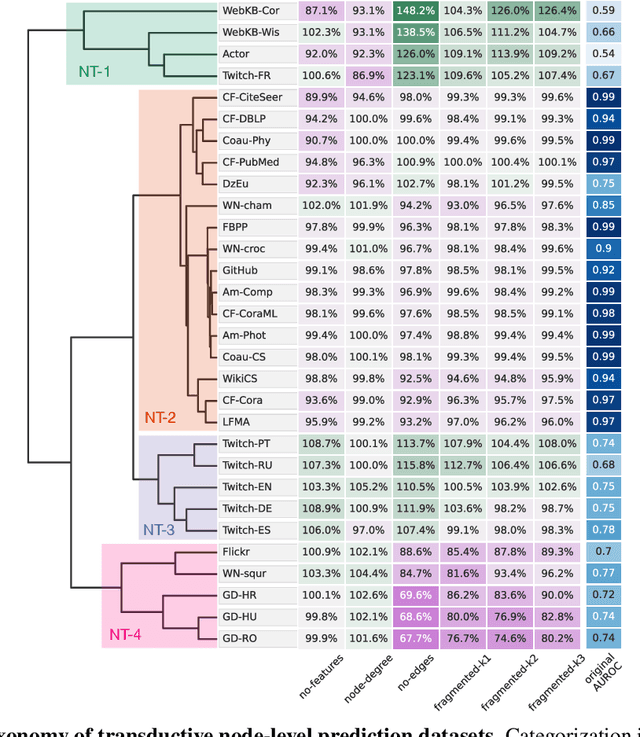
Graph neural networks (GNNs) have attracted much attention due to their ability to leverage the intrinsic geometries of the underlying data. Although many different types of GNN models have been developed, with many benchmarking procedures to demonstrate the superiority of one GNN model over the others, there is a lack of systematic understanding of the underlying benchmarking datasets, and what aspects of the model are being tested. Here, we provide a principled approach to taxonomize graph benchmarking datasets by carefully designing a collection of graph perturbations to probe the essential data characteristics that GNN models leverage to perform predictions. Our data-driven taxonomization of graph datasets provides a new understanding of critical dataset characteristics that will enable better model evaluation and the development of more specialized GNN models.

Evaluation Metrics for Graph Generative Models: Problems, Pitfalls, and Practical Solutions

Graph generative models are a highly active branch of machine learning. Given the steady development of new models of ever-increasing complexity, it is necessary to provide a principled way to evaluate and compare them. In this paper, we enumerate the desirable criteria for comparison metrics, discuss the development of such metrics, and provide a comparison of their respective expressive power. We perform a systematic evaluation of the main metrics in use today, highlighting some of the challenges and pitfalls researchers inadvertently can run into. We then describe a collection of suitable metrics, give recommendations as to their practical suitability, and analyse their behaviour on synthetically generated perturbed graphs as well as on recently proposed graph generative models.

Graph Kernels: State-of-the-Art and Future Challenges

Graph-structured data are an integral part of many application domains, including chemoinformatics, computational biology, neuroimaging, and social network analysis. Over the last two decades, numerous graph kernels, i.e. kernel functions between graphs, have been proposed to solve the problem of assessing the similarity between graphs, thereby making it possible to perform predictions in both classification and regression settings. This manuscript provides a review of existing graph kernels, their applications, software plus data resources, and an empirical comparison of state-of-the-art graph kernels.