Inherently Interpretable Time Series Classification via Multiple Instance Learning

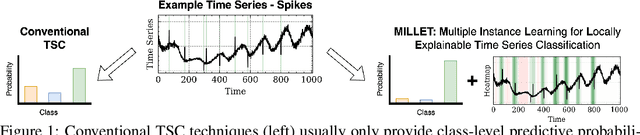
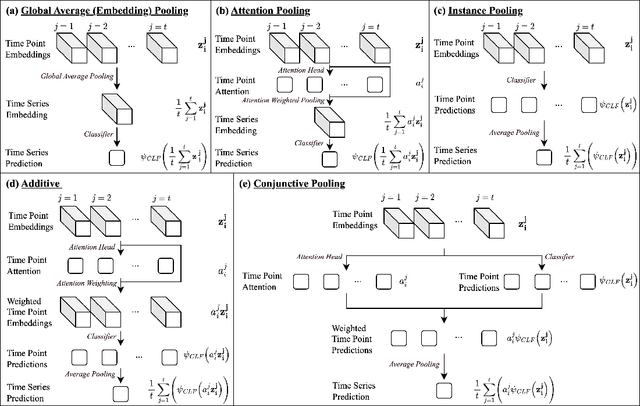
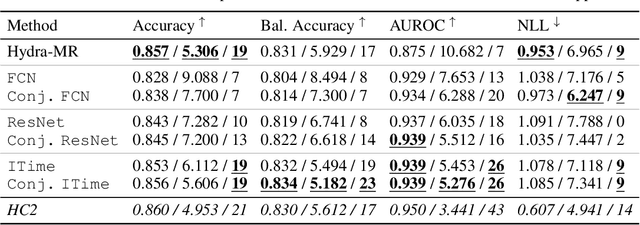
Conventional Time Series Classification (TSC) methods are often black boxes that obscure inherent interpretation of their decision-making processes. In this work, we leverage Multiple Instance Learning (MIL) to overcome this issue, and propose a new framework called MILLET: Multiple Instance Learning for Locally Explainable Time series classification. We apply MILLET to existing deep learning TSC models and show how they become inherently interpretable without compromising (and in some cases, even improving) predictive performance. We evaluate MILLET on 85 UCR TSC datasets and also present a novel synthetic dataset that is specially designed to facilitate interpretability evaluation. On these datasets, we show MILLET produces sparse explanations quickly that are of higher quality than other well-known interpretability methods. To the best of our knowledge, our work with MILLET, which is available on GitHub (https://github.com/JAEarly/MILTimeSeriesClassification), is the first to develop general MIL methods for TSC and apply them to an extensive variety of domains

Low-count Time Series Anomaly Detection

Low-count time series describe sparse or intermittent events, which are prevalent in large-scale online platforms that capture and monitor diverse data types. Several distinct challenges surface when modelling low-count time series, particularly low signal-to-noise ratios (when anomaly signatures are provably undetectable), and non-uniform performance (when average metrics are not representative of local behaviour). The time series anomaly detection community currently lacks explicit tooling and processes to model and reliably detect anomalies in these settings. We address this gap by introducing a novel generative procedure for creating benchmark datasets comprising of low-count time series with anomalous segments. Via a mixture of theoretical and empirical analysis, our work explains how widely-used algorithms struggle with the distribution overlap between normal and anomalous segments. In order to mitigate this shortcoming, we then leverage our findings to demonstrate how anomaly score smoothing consistently improves performance. The practical utility of our analysis and recommendation is validated on a real-world dataset containing sales data for retail stores.

Deep Gaussian Processes for Multi-fidelity Modeling

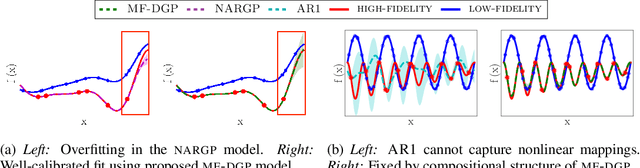
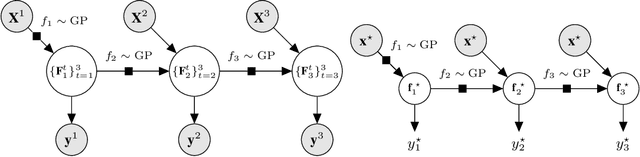
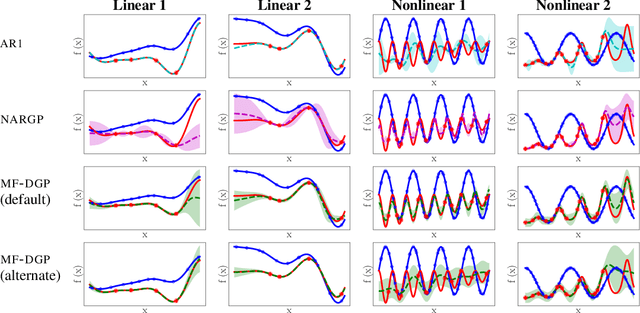
Multi-fidelity methods are prominently used when cheaply-obtained, but possibly biased and noisy, observations must be effectively combined with limited or expensive true data in order to construct reliable models. This arises in both fundamental machine learning procedures such as Bayesian optimization, as well as more practical science and engineering applications. In this paper we develop a novel multi-fidelity model which treats layers of a deep Gaussian process as fidelity levels, and uses a variational inference scheme to propagate uncertainty across them. This allows for capturing nonlinear correlations between fidelities with lower risk of overfitting than existing methods exploiting compositional structure, which are conversely burdened by structural assumptions and constraints. We show that the proposed approach makes substantial improvements in quantifying and propagating uncertainty in multi-fidelity set-ups, which in turn improves their effectiveness in decision making pipelines.

Entropic Trace Estimates for Log Determinants

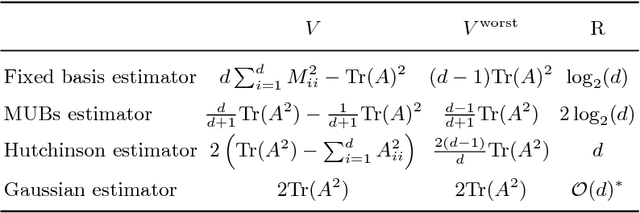
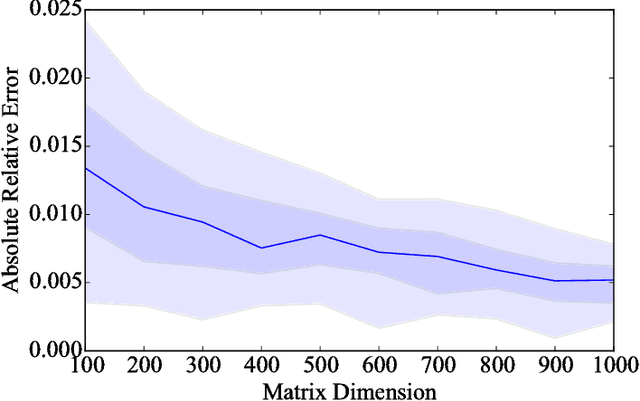
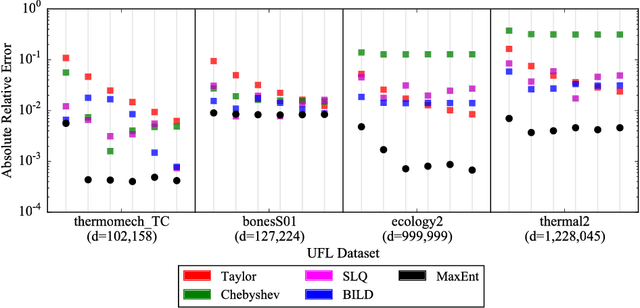
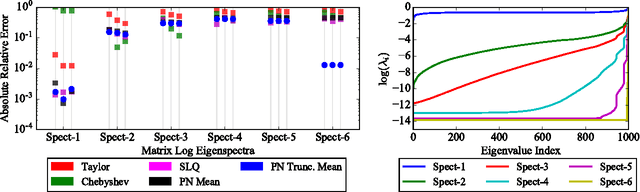
The scalable calculation of matrix determinants has been a bottleneck to the widespread application of many machine learning methods such as determinantal point processes, Gaussian processes, generalised Markov random fields, graph models and many others. In this work, we estimate log determinants under the framework of maximum entropy, given information in the form of moment constraints from stochastic trace estimation. The estimates demonstrate a significant improvement on state-of-the-art alternative methods, as shown on a wide variety of UFL sparse matrices. By taking the example of a general Markov random field, we also demonstrate how this approach can significantly accelerate inference in large-scale learning methods involving the log determinant.

Bayesian Inference of Log Determinants

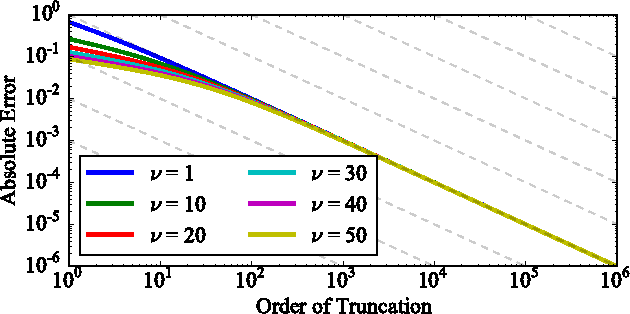
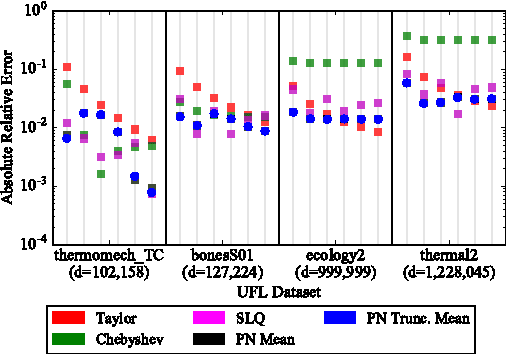
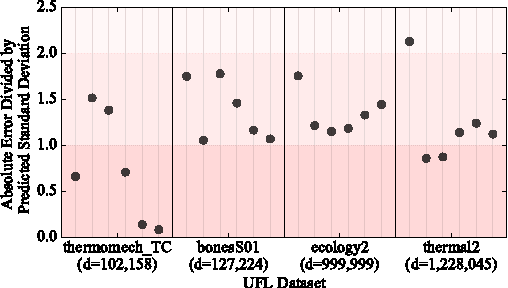
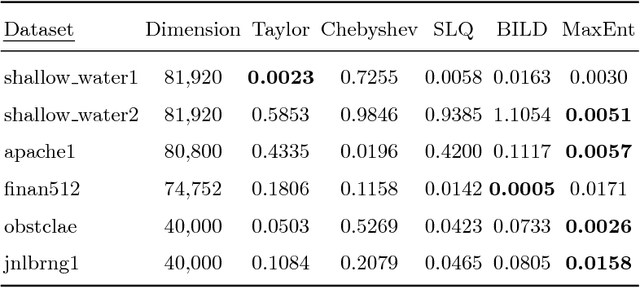
The log-determinant of a kernel matrix appears in a variety of machine learning problems, ranging from determinantal point processes and generalized Markov random fields, through to the training of Gaussian processes. Exact calculation of this term is often intractable when the size of the kernel matrix exceeds a few thousand. In the spirit of probabilistic numerics, we reinterpret the problem of computing the log-determinant as a Bayesian inference problem. In particular, we combine prior knowledge in the form of bounds from matrix theory and evidence derived from stochastic trace estimation to obtain probabilistic estimates for the log-determinant and its associated uncertainty within a given computational budget. Beyond its novelty and theoretic appeal, the performance of our proposal is competitive with state-of-the-art approaches to approximating the log-determinant, while also quantifying the uncertainty due to budget-constrained evidence.

AutoGP: Exploring the Capabilities and Limitations of Gaussian Process Models

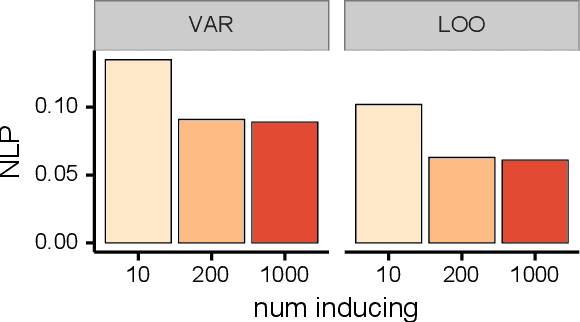
We investigate the capabilities and limitations of Gaussian process models by jointly exploring three complementary directions: (i) scalable and statistically efficient inference; (ii) flexible kernels; and (iii) objective functions for hyperparameter learning alternative to the marginal likelihood. Our approach outperforms all previously reported GP methods on the standard MNIST dataset; performs comparatively to previous kernel-based methods using the RECTANGLES-IMAGE dataset; and breaks the 1% error-rate barrier in GP models using the MNIST8M dataset, showing along the way the scalability of our method at unprecedented scale for GP models (8 million observations) in classification problems. Overall, our approach represents a significant breakthrough in kernel methods and GP models, bridging the gap between deep learning approaches and kernel machines.

Random Feature Expansions for Deep Gaussian Processes

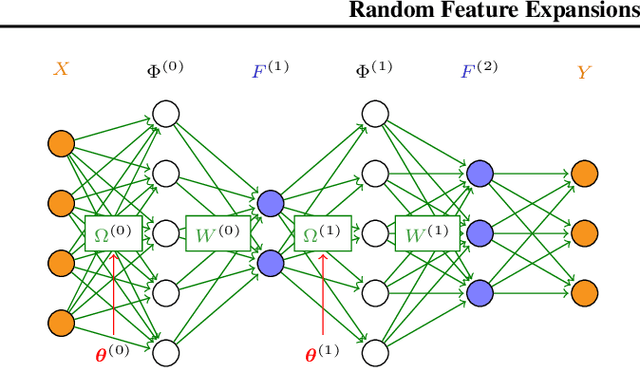
The composition of multiple Gaussian Processes as a Deep Gaussian Process (DGP) enables a deep probabilistic nonparametric approach to flexibly tackle complex machine learning problems with sound quantification of uncertainty. Existing inference approaches for DGP models have limited scalability and are notoriously cumbersome to construct. In this work, we introduce a novel formulation of DGPs based on random feature expansions that we train using stochastic variational inference. This yields a practical learning framework which significantly advances the state-of-the-art in inference for DGPs, and enables accurate quantification of uncertainty. We extensively showcase the scalability and performance of our proposal on several datasets with up to 8 million observations, and various DGP architectures with up to 30 hidden layers.

Preconditioning Kernel Matrices

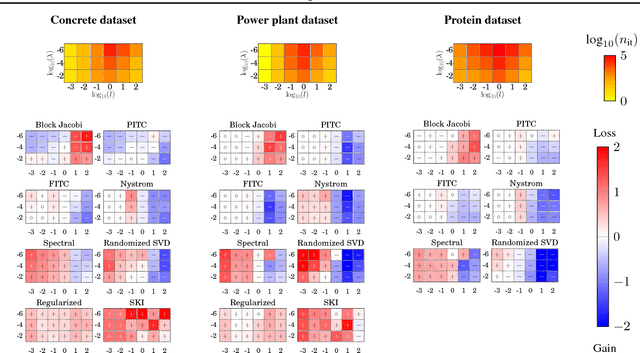
The computational and storage complexity of kernel machines presents the primary barrier to their scaling to large, modern, datasets. A common way to tackle the scalability issue is to use the conjugate gradient algorithm, which relieves the constraints on both storage (the kernel matrix need not be stored) and computation (both stochastic gradients and parallelization can be used). Even so, conjugate gradient is not without its own issues: the conditioning of kernel matrices is often such that conjugate gradients will have poor convergence in practice. Preconditioning is a common approach to alleviating this issue. Here we propose preconditioned conjugate gradients for kernel machines, and develop a broad range of preconditioners particularly useful for kernel matrices. We describe a scalable approach to both solving kernel machines and learning their hyperparameters. We show this approach is exact in the limit of iterations and outperforms state-of-the-art approximations for a given computational budget.