Deep Gaussian Processes for Multi-fidelity Modeling
Paper and Code
Mar 18, 2019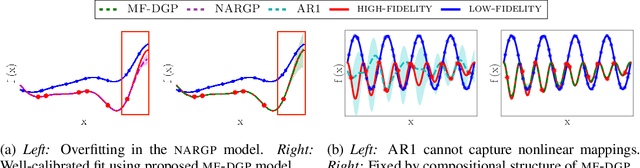

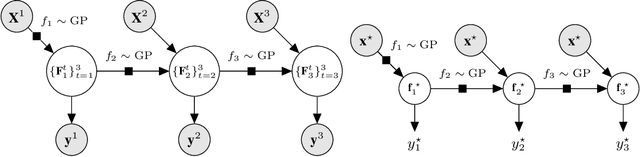
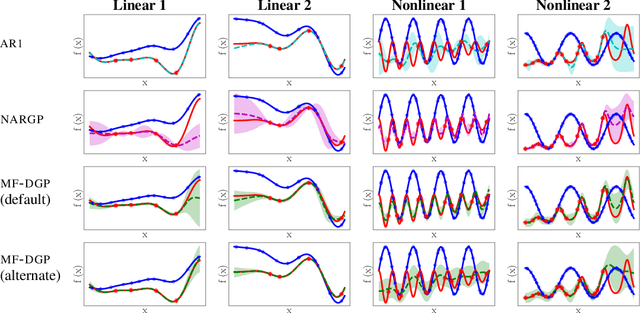
Multi-fidelity methods are prominently used when cheaply-obtained, but possibly biased and noisy, observations must be effectively combined with limited or expensive true data in order to construct reliable models. This arises in both fundamental machine learning procedures such as Bayesian optimization, as well as more practical science and engineering applications. In this paper we develop a novel multi-fidelity model which treats layers of a deep Gaussian process as fidelity levels, and uses a variational inference scheme to propagate uncertainty across them. This allows for capturing nonlinear correlations between fidelities with lower risk of overfitting than existing methods exploiting compositional structure, which are conversely burdened by structural assumptions and constraints. We show that the proposed approach makes substantial improvements in quantifying and propagating uncertainty in multi-fidelity set-ups, which in turn improves their effectiveness in decision making pipelines.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge