AutoGP: Exploring the Capabilities and Limitations of Gaussian Process Models
Paper and Code
Mar 06, 2017
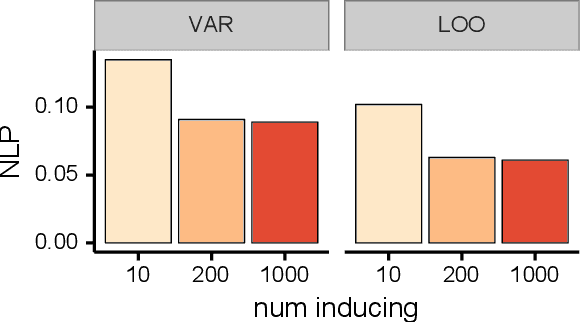
We investigate the capabilities and limitations of Gaussian process models by jointly exploring three complementary directions: (i) scalable and statistically efficient inference; (ii) flexible kernels; and (iii) objective functions for hyperparameter learning alternative to the marginal likelihood. Our approach outperforms all previously reported GP methods on the standard MNIST dataset; performs comparatively to previous kernel-based methods using the RECTANGLES-IMAGE dataset; and breaks the 1% error-rate barrier in GP models using the MNIST8M dataset, showing along the way the scalability of our method at unprecedented scale for GP models (8 million observations) in classification problems. Overall, our approach represents a significant breakthrough in kernel methods and GP models, bridging the gap between deep learning approaches and kernel machines.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge