Naturally Private Recommendations with Determinantal Point Processes

Often we consider machine learning models or statistical analysis methods which we endeavour to alter, by introducing a randomized mechanism, to make the model conform to a differential privacy constraint. However, certain models can often be implicitly differentially private or require significantly fewer alterations. In this work, we discuss Determinantal Point Processes (DPPs) which are dispersion models that balance recommendations based on both the popularity and the diversity of the content. We introduce DPPs, derive and discuss the alternations required for them to satisfy epsilon-Differential Privacy and provide an analysis of their sensitivity. We conclude by proposing simple alternatives to DPPs which would make them more efficient with respect to their privacy-utility trade-off.

Intersectionality: Multiple Group Fairness in Expectation Constraints

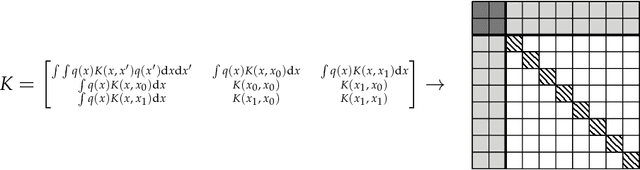
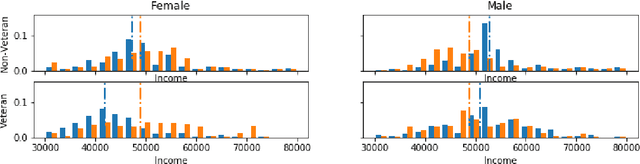
Group fairness is an important concern for machine learning researchers, developers, and regulators. However, the strictness to which models must be constrained to be considered fair is still under debate. The focus of this work is on constraining the expected outcome of subpopulations in kernel regression and, in particular, decision tree regression, with application to random forests, boosted trees and other ensemble models. While individual constraints were previously addressed, this work addresses concerns about incorporating multiple constraints simultaneously. The proposed solution does not affect the order of computational or memory complexity of the decision trees and is easily integrated into models post training.

Equality Constrained Decision Trees: For the Algorithmic Enforcement of Group Fairness

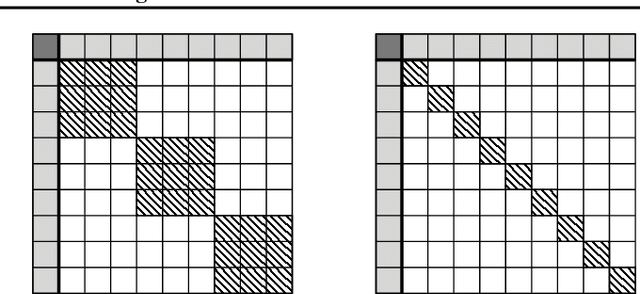
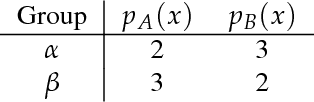
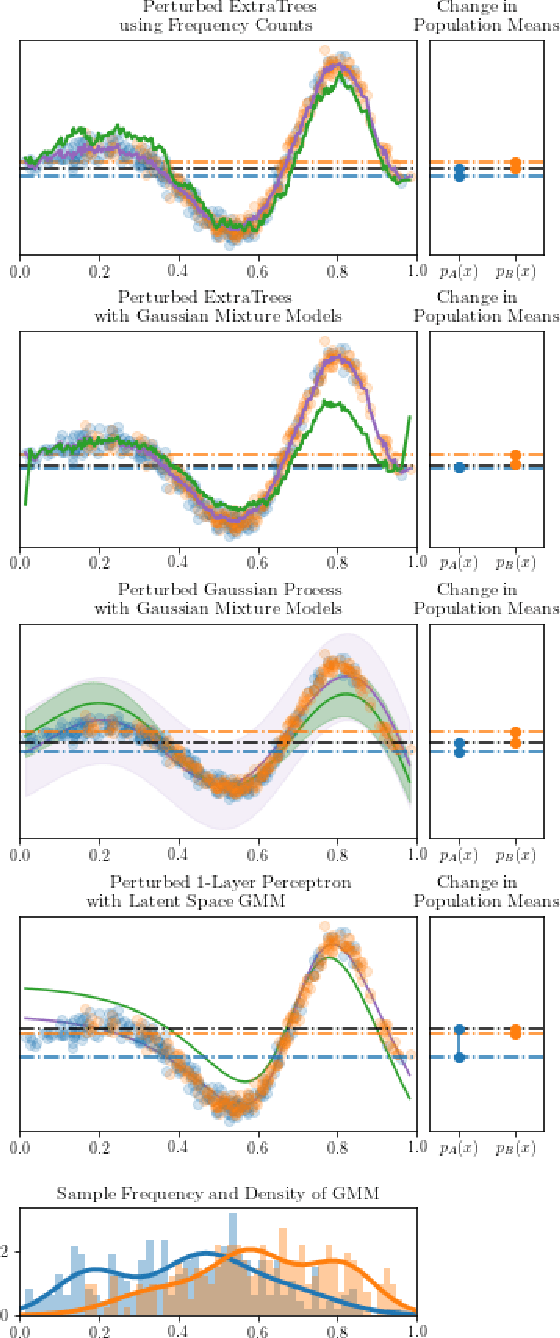
Fairness, through its many forms and definitions, has become an important issue facing the machine learning community. In this work, we consider how to incorporate group fairness constraints in kernel regression methods. More specifically, we focus on examining the incorporation of these constraints in decision tree regression when cast as a form of kernel regression, with direct applications to random forests and boosted trees amongst other widespread popular inference techniques. We show that order of complexity of memory and computation is preserved for such models and bounds the expected perturbations to the model in terms of the number of leaves of the trees. Importantly, the approach works on trained models and hence can be easily applied to models in current use.

Entropic Trace Estimates for Log Determinants

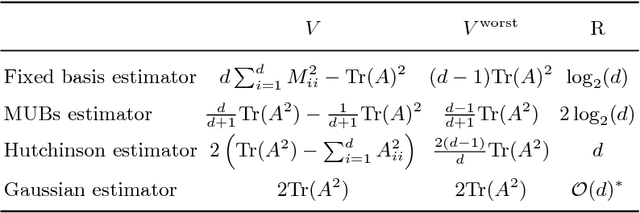
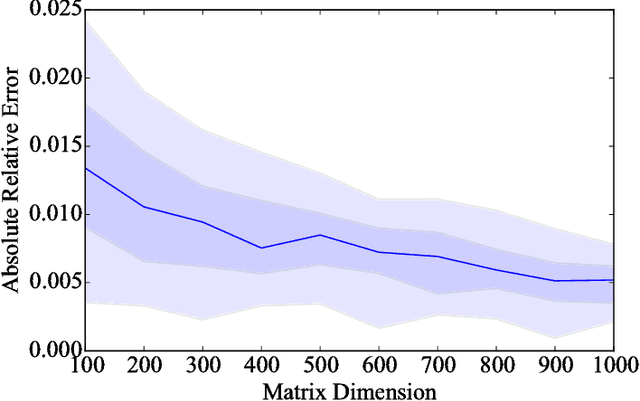
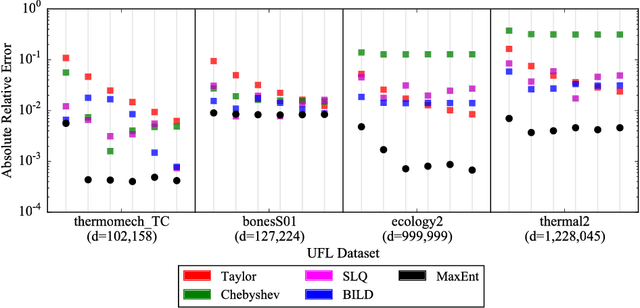
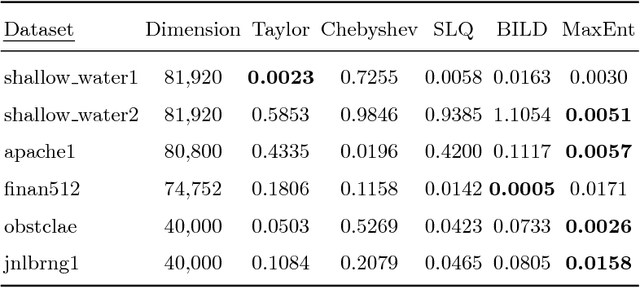
The scalable calculation of matrix determinants has been a bottleneck to the widespread application of many machine learning methods such as determinantal point processes, Gaussian processes, generalised Markov random fields, graph models and many others. In this work, we estimate log determinants under the framework of maximum entropy, given information in the form of moment constraints from stochastic trace estimation. The estimates demonstrate a significant improvement on state-of-the-art alternative methods, as shown on a wide variety of UFL sparse matrices. By taking the example of a general Markov random field, we also demonstrate how this approach can significantly accelerate inference in large-scale learning methods involving the log determinant.

Bayesian Inference of Log Determinants

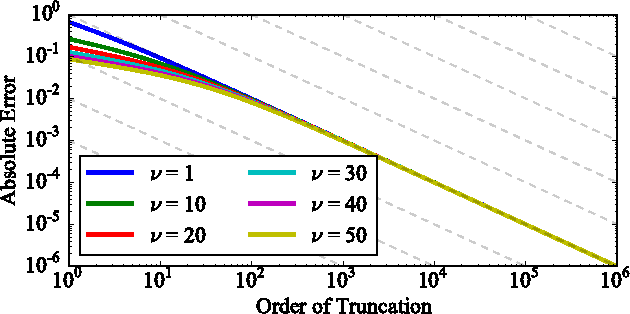
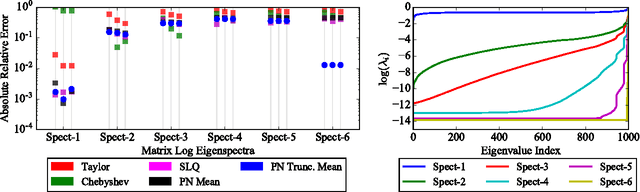
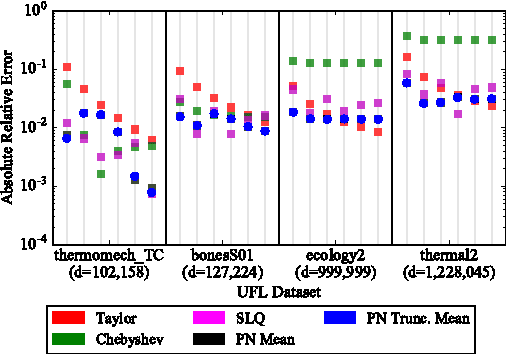
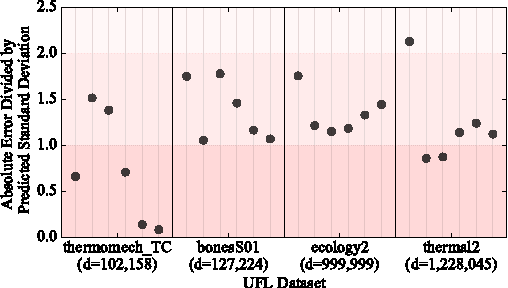
The log-determinant of a kernel matrix appears in a variety of machine learning problems, ranging from determinantal point processes and generalized Markov random fields, through to the training of Gaussian processes. Exact calculation of this term is often intractable when the size of the kernel matrix exceeds a few thousand. In the spirit of probabilistic numerics, we reinterpret the problem of computing the log-determinant as a Bayesian inference problem. In particular, we combine prior knowledge in the form of bounds from matrix theory and evidence derived from stochastic trace estimation to obtain probabilistic estimates for the log-determinant and its associated uncertainty within a given computational budget. Beyond its novelty and theoretic appeal, the performance of our proposal is competitive with state-of-the-art approaches to approximating the log-determinant, while also quantifying the uncertainty due to budget-constrained evidence.