Equality Constrained Decision Trees: For the Algorithmic Enforcement of Group Fairness
Paper and Code
Oct 10, 2018
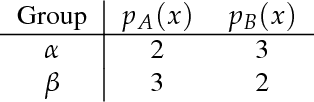
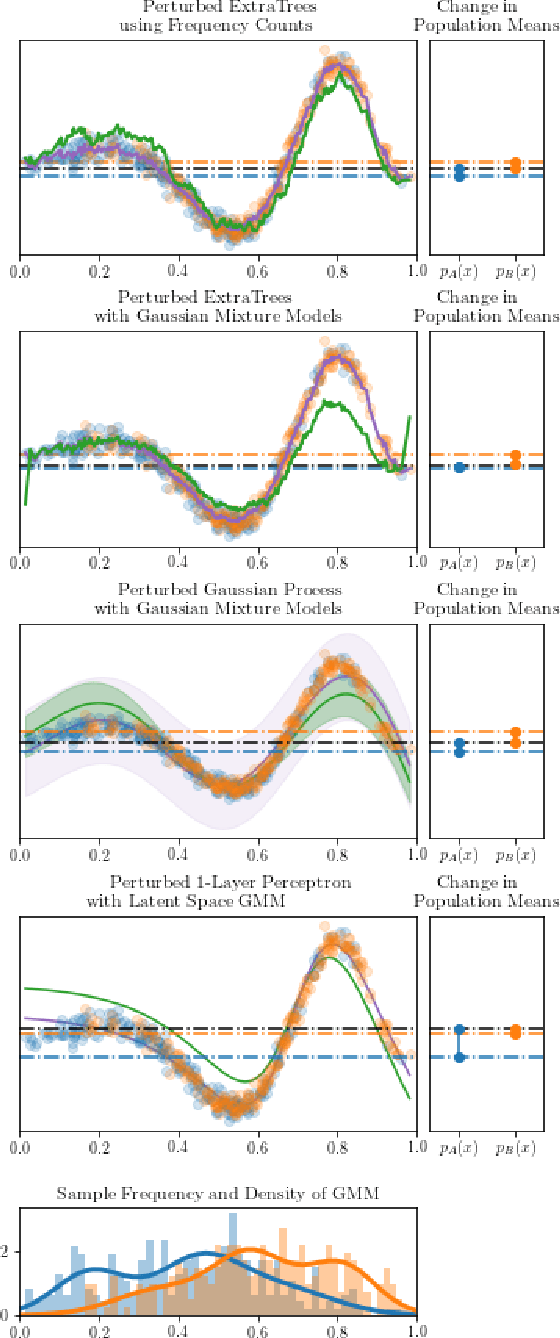

Fairness, through its many forms and definitions, has become an important issue facing the machine learning community. In this work, we consider how to incorporate group fairness constraints in kernel regression methods. More specifically, we focus on examining the incorporation of these constraints in decision tree regression when cast as a form of kernel regression, with direct applications to random forests and boosted trees amongst other widespread popular inference techniques. We show that order of complexity of memory and computation is preserved for such models and bounds the expected perturbations to the model in terms of the number of leaves of the trees. Importantly, the approach works on trained models and hence can be easily applied to models in current use.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge