Inductive Learning for Possibilistic Logic Programs Under Stable Models

Possibilistic logic programs (poss-programs) under stable models are a major variant of answer set programming (ASP). While its semantics (possibilistic stable models) and properties have been well investigated, the problem of inductive reasoning has not been investigated yet. This paper presents an approach to extracting poss-programs from a background program and examples (parts of intended possibilistic stable models). To this end, the notion of induction tasks is first formally defined, its properties are investigated and two algorithms ilpsm and ilpsmmin for computing induction solutions are presented. An implementation of ilpsmmin is also provided and experimental results show that when inputs are ordinary logic programs, the prototype outperforms a major inductive learning system for normal logic programs from stable models on the datasets that are randomly generated.

Task Progressive Curriculum Learning for Robust Visual Question Answering

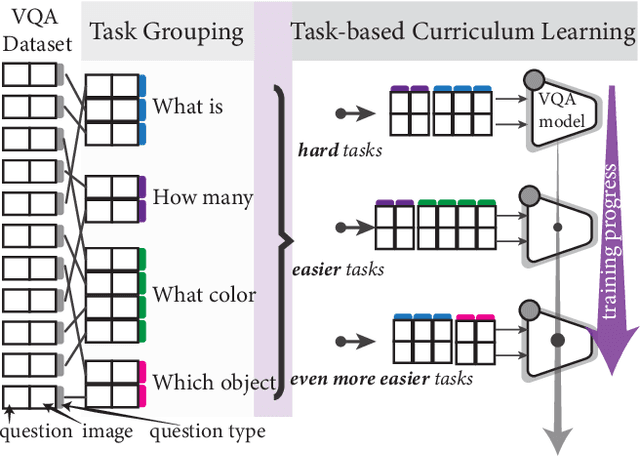
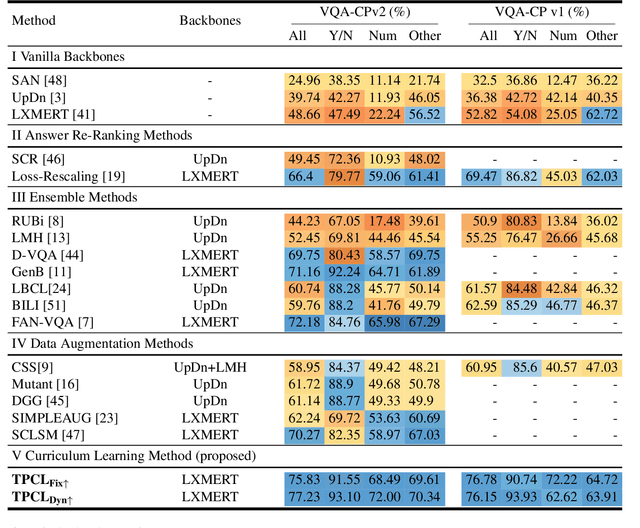
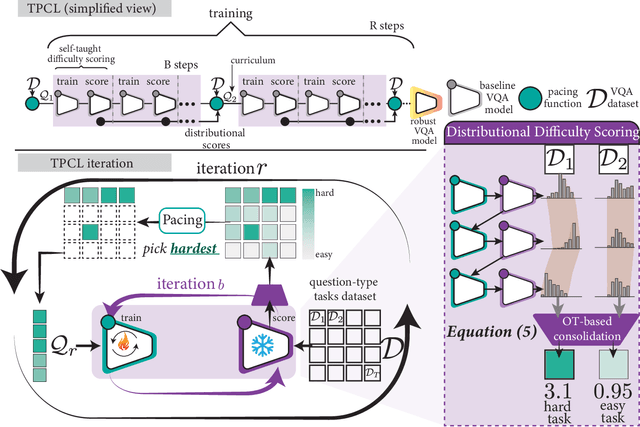
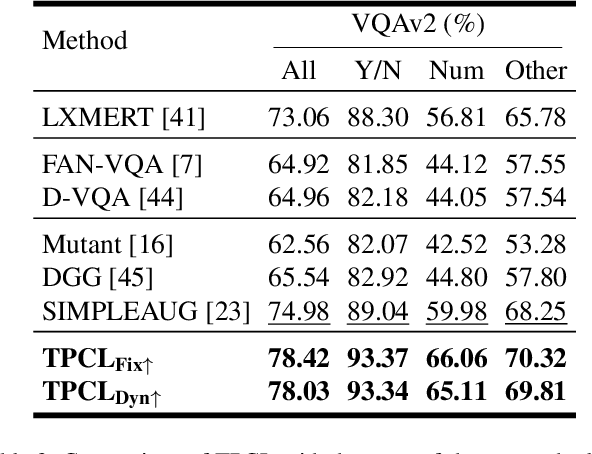
Visual Question Answering (VQA) systems are known for their poor performance in out-of-distribution datasets. An issue that was addressed in previous works through ensemble learning, answer re-ranking, or artificially growing the training set. In this work, we show for the first time that robust Visual Question Answering is attainable by simply enhancing the training strategy. Our proposed approach, Task Progressive Curriculum Learning (TPCL), breaks the main VQA problem into smaller, easier tasks based on the question type. Then, it progressively trains the model on a (carefully crafted) sequence of tasks. We further support the method by a novel distributional-based difficulty measurer. Our approach is conceptually simple, model-agnostic, and easy to implement. We demonstrate TPCL effectiveness through a comprehensive evaluation on standard datasets. Without either data augmentation or explicit debiasing mechanism, it achieves state-of-the-art on VQA-CP v2, VQA-CP v1 and VQA v2 datasets. Extensive experiments demonstrate that TPCL outperforms the most competitive robust VQA approaches by more than 5% and 7% on VQA-CP v2 and VQA-CP v1; respectively. TPCL also can boost VQA baseline backbone performance by up to 28.5%.

Differentiating Choices via Commonality for Multiple-Choice Question Answering

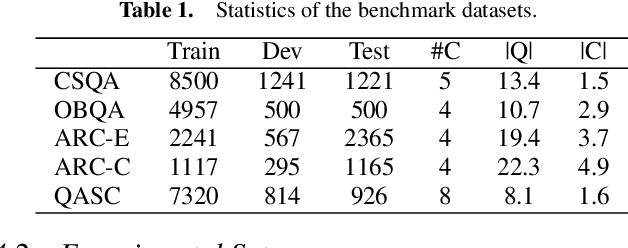
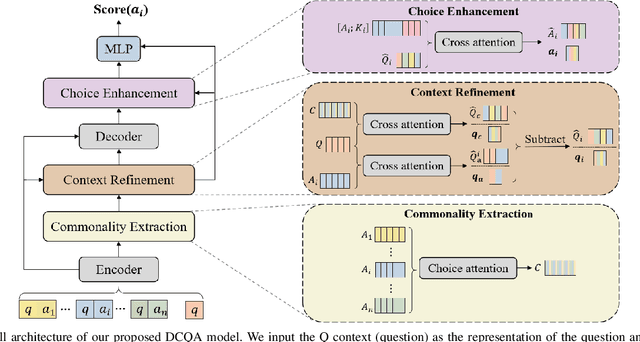
Multiple-choice question answering (MCQA) becomes particularly challenging when all choices are relevant to the question and are semantically similar. Yet this setting of MCQA can potentially provide valuable clues for choosing the right answer. Existing models often rank each choice separately, overlooking the context provided by other choices. Specifically, they fail to leverage the semantic commonalities and nuances among the choices for reasoning. In this paper, we propose a novel MCQA model by differentiating choices through identifying and eliminating their commonality, called DCQA. Our model captures token-level attention of each choice to the question, and separates tokens of the question attended to by all the choices (i.e., commonalities) from those by individual choices (i.e., nuances). Using the nuances as refined contexts for the choices, our model can effectively differentiate choices with subtle differences and provide justifications for choosing the correct answer. We conduct comprehensive experiments across five commonly used MCQA benchmarks, demonstrating that DCQA consistently outperforms baseline models. Furthermore, our case study illustrates the effectiveness of the approach in directing the attention of the model to more differentiating features.

Function-words Enhanced Attention Networks for Few-Shot Inverse Relation Classification

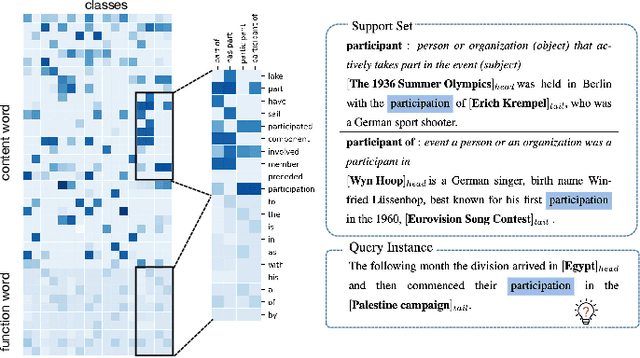
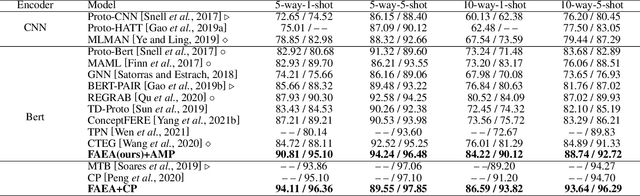
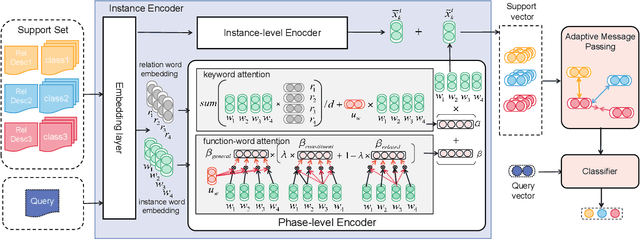
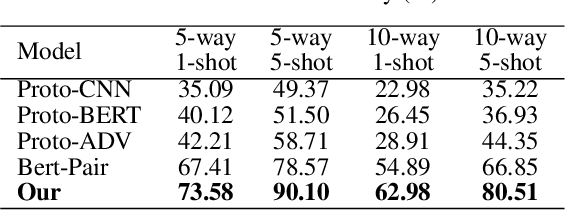
The relation classification is to identify semantic relations between two entities in a given text. While existing models perform well for classifying inverse relations with large datasets, their performance is significantly reduced for few-shot learning. In this paper, we propose a function words adaptively enhanced attention framework (FAEA) for few-shot inverse relation classification, in which a hybrid attention model is designed to attend class-related function words based on meta-learning. As the involvement of function words brings in significant intra-class redundancy, an adaptive message passing mechanism is introduced to capture and transfer inter-class differences.We mathematically analyze the negative impact of function words from dot-product measurement, which explains why message passing mechanism effectively reduces the impact. Our experimental results show that FAEA outperforms strong baselines, especially the inverse relation accuracy is improved by 14.33% under 1-shot setting in FewRel1.0.

Knowledge Compilation in Multi-Agent Epistemic Logics

Epistemic logics are a primary formalism for multi-agent systems but major reasoning tasks in such epistemic logics are intractable, which impedes applications of multi-agent epistemic logics in automatic planning. Knowledge compilation provides a promising way of resolving the intractability by identifying expressive fragments of epistemic logics that are tractable for important reasoning tasks such as satisfiability and forgetting. The property of logical separability allows to decompose a formula into some of its subformulas and thus modular algorithms for various reasoning tasks can be developed. In this paper, by employing logical separability, we propose an approach to knowledge compilation for the logic Kn by defining a normal form SDNF. Among several novel results, we show that every epistemic formula can be equivalently compiled into a formula in SDNF, major reasoning tasks in SDNF are tractable, and formulas in SDNF enjoy the logical separability. Our results shed some lights on modular approaches to knowledge compilation. Furthermore, we apply our results in the multi-agent epistemic planning. Finally, we extend the above result to the logic K45n that is Kn extended by introspection axioms 4 and 5.

Syntax-Preserving Belief Change Operators for Logic Programs

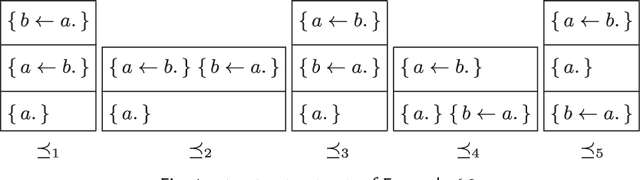
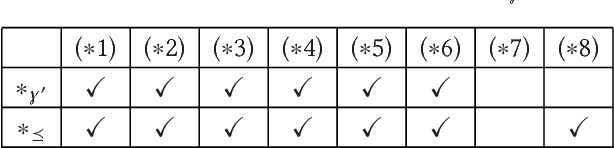
Recent methods have adapted the well-established AGM and belief base frameworks for belief change to cover belief revision in logic programs. In this study here, we present two new sets of belief change operators for logic programs. They focus on preserving the explicit relationships expressed in the rules of a program, a feature that is missing in purely semantic approaches that consider programs only in their entirety. In particular, operators of the latter class fail to satisfy preservation and support, two important properties for belief change in logic programs required to ensure intuitive results. We address this shortcoming of existing approaches by introducing partial meet and ensconcement constructions for logic program belief change, which allow us to define syntax-preserving operators that satisfy preservation and support. Our work is novel in that our constructions not only preserve more information from a logic program during a change operation than existing ones, but they also facilitate natural definitions of contraction operators, the first in the field to the best of our knowledge. In order to evaluate the rationality of our operators, we translate the revision and contraction postulates from the AGM and belief base frameworks to the logic programming setting. We show that our operators fully comply with the belief base framework and formally state the interdefinability between our operators. We further propose an algorithm that is based on modularising a logic program to reduce partial meet and ensconcement revisions or contractions to performing the operation only on the relevant modules of that program. Finally, we compare our approach to two state-of-the-art logic program revision methods and demonstrate that our operators address the shortcomings of one and generalise the other method.

A Distance-based Paraconsistent Semantics for DL-Lite

DL-Lite is an important family of description logics. Recently, there is an increasing interest in handling inconsistency in DL-Lite as the constraint imposed by a TBox can be easily violated by assertions in ABox in DL-Lite. In this paper, we present a distance-based paraconsistent semantics based on the notion of feature in DL-Lite, which provides a novel way to rationally draw meaningful conclusions even from an inconsistent knowledge base. Finally, we investigate several important logical properties of this entailment relation based on the new semantics and show its promising advantages in non-monotonic reasoning for DL-Lite.

Preferential Multi-Context Systems

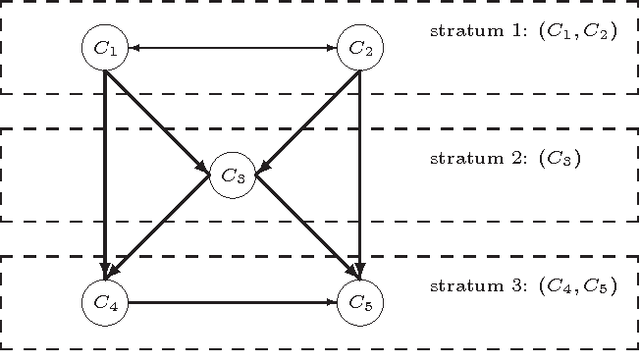
Multi-context systems (MCS) presented by Brewka and Eiter can be considered as a promising way to interlink decentralized and heterogeneous knowledge contexts. In this paper, we propose preferential multi-context systems (PMCS), which provide a framework for incorporating a total preorder relation over contexts in a multi-context system. In a given PMCS, its contexts are divided into several parts according to the total preorder relation over them, moreover, only information flows from a context to ones of the same part or less preferred parts are allowed to occur. As such, the first $l$ preferred parts of an PMCS always fully capture the information exchange between contexts of these parts, and then compose another meaningful PMCS, termed the $l$-section of that PMCS. We generalize the equilibrium semantics for an MCS to the (maximal) $l_{\leq}$-equilibrium which represents belief states at least acceptable for the $l$-section of an PMCS. We also investigate inconsistency analysis in PMCS and related computational complexity issues.

Random Logic Programs: Linear Model

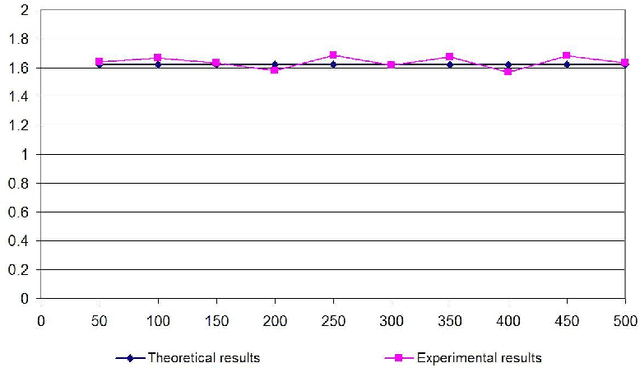
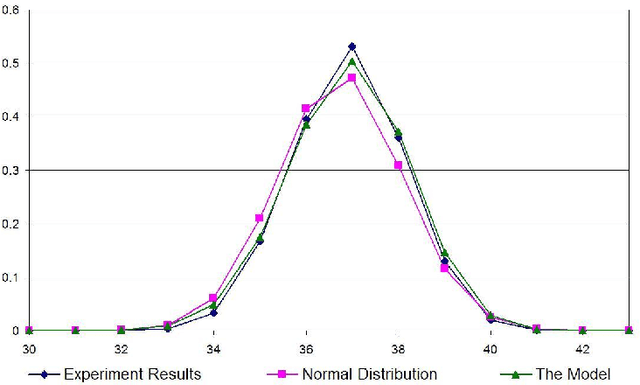
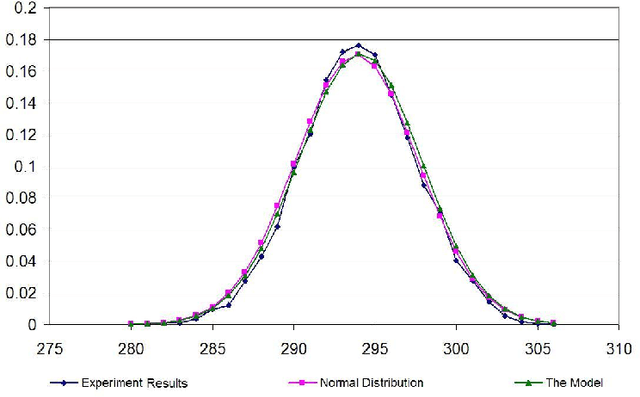
This paper proposes a model, the linear model, for randomly generating logic programs with low density of rules and investigates statistical properties of such random logic programs. It is mathematically shown that the average number of answer sets for a random program converges to a constant when the number of atoms approaches infinity. Several experimental results are also reported, which justify the suitability of the linear model. It is also experimentally shown that, under this model, the size distribution of answer sets for random programs tends to a normal distribution when the number of atoms is sufficiently large.

An Approach to Forgetting in Disjunctive Logic Programs that Preserves Strong Equivalence

In this paper we investigate forgetting in disjunctive logic programs, where forgetting an atom from a program amounts to a reduction in the signature of that program. The goal is to provide an approach that is syntax-independent, in that if two programs are strongly equivalent, then the results of forgetting an atom in each program should also be strongly equivalent. Our central definition of forgetting is impractical but satisfies this goal: Forgetting an atom is characterised by the set of SE consequences of the program that do not mention the atom to be forgotten. We then provide an equivalent, practical definition, wherein forgetting an atom $p$ is given by those rules in the program that don't mention $p$, together with rules obtained by a single inference step from rules that do mention $p$. Forgetting is shown to have appropriate properties; as well, the finite characterisation results in a modest (at worst quadratic) blowup. Finally we have also obtained a prototype implementation of this approach to forgetting.