AdaHAT: Adaptive Hard Attention to the Task in Task-Incremental Learning

Catastrophic forgetting is a major problem in task-incremental learning, where neural networks tend to overwrite previously learned knowledge when trained on new tasks. A number of architecture-based approaches have been proposed to address this problem. However, the architecture-based approaches suffer from another problem related to network capacity when the networks learn long task sequences: As a network is trained on an increasing number of new tasks in a long task sequence, a growing proportion of active parameters becomes static to prevent forgetting of previously learned knowledge. In this paper, we propose Adaptive Hard Attention to the Task (AdaHAT) with an adaptive attention mechanism which allows adaptive updates to static parameters by taking into account the information about previous tasks on both the importance of these parameters to previous tasks and the current network capacity. Based on this idea, we develop a new neural network architecture incorporating our proposed AdaHAT mechanism. AdaHAT extends an existing architecture-based approach, Hard Attention to the Task (HAT), to better support task-incremental learning over long task sequences. We conduct experiments on a number of datasets and compare AdaHAT with task-incremental learning baselines including HAT. Our experimental results show that AdaHAT achieves better average performance across tasks than these baselines, especially on long task sequences, demonstrating the benefits from balancing the trade-off between stability and plasticity of a network when learning such sequences of tasks, alleviating the network capacity problem. Our code is available at pengxiang-wang.com/projects/continual-learning-arena.

Preferential Multi-Context Systems

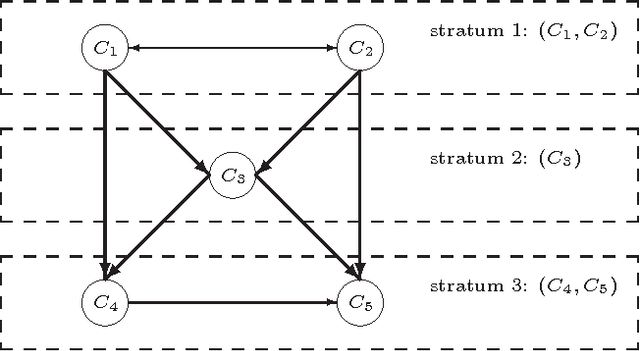
Multi-context systems (MCS) presented by Brewka and Eiter can be considered as a promising way to interlink decentralized and heterogeneous knowledge contexts. In this paper, we propose preferential multi-context systems (PMCS), which provide a framework for incorporating a total preorder relation over contexts in a multi-context system. In a given PMCS, its contexts are divided into several parts according to the total preorder relation over them, moreover, only information flows from a context to ones of the same part or less preferred parts are allowed to occur. As such, the first $l$ preferred parts of an PMCS always fully capture the information exchange between contexts of these parts, and then compose another meaningful PMCS, termed the $l$-section of that PMCS. We generalize the equilibrium semantics for an MCS to the (maximal) $l_{\leq}$-equilibrium which represents belief states at least acceptable for the $l$-section of an PMCS. We also investigate inconsistency analysis in PMCS and related computational complexity issues.

Random Logic Programs: Linear Model

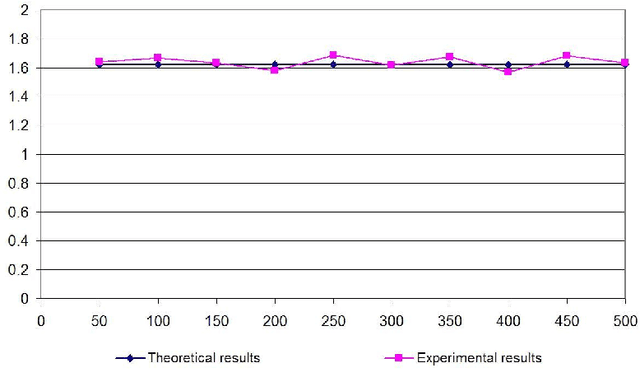
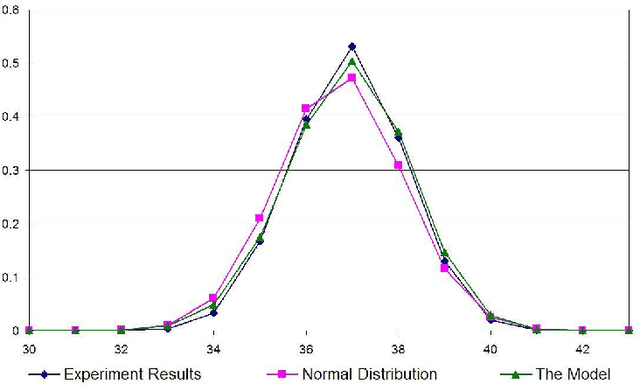
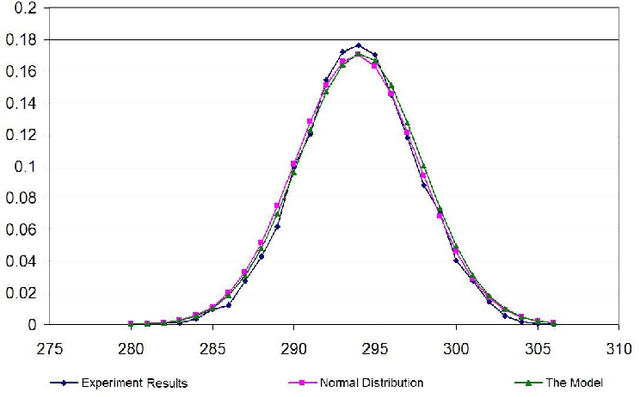
This paper proposes a model, the linear model, for randomly generating logic programs with low density of rules and investigates statistical properties of such random logic programs. It is mathematically shown that the average number of answer sets for a random program converges to a constant when the number of atoms approaches infinity. Several experimental results are also reported, which justify the suitability of the linear model. It is also experimentally shown that, under this model, the size distribution of answer sets for random programs tends to a normal distribution when the number of atoms is sufficiently large.