Evaluating GPT's Programming Capability through CodeWars' Katas

In the burgeoning field of artificial intelligence (AI), understanding the capabilities and limitations of programming-oriented models is crucial. This paper presents a novel evaluation of the programming proficiency of Generative Pretrained Transformer (GPT) models, specifically GPT-3.5 and GPT-4, against coding problems of varying difficulty levels drawn from Codewars. The experiments reveal a distinct boundary at the 3kyu level, beyond which these GPT models struggle to provide solutions. These findings led to the proposal of a measure for coding problem complexity that incorporates both problem difficulty and the time required for solution. The research emphasizes the need for validation and creative thinking capabilities in AI models to better emulate human problem-solving techniques. Future work aims to refine this proposed complexity measure, enhance AI models with these suggested capabilities, and develop an objective measure for programming problem difficulty. The results of this research offer invaluable insights for improving AI programming capabilities and advancing the frontier of AI problem-solving abilities.

On the Sampling Strategy for Evaluation of Spectral-spatial Methods in Hyperspectral Image Classification

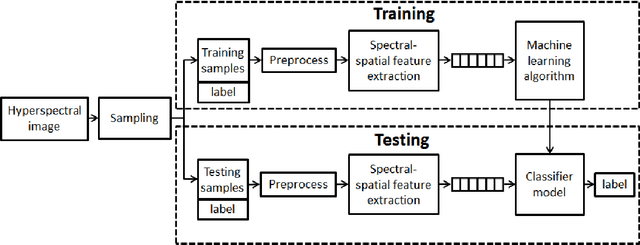
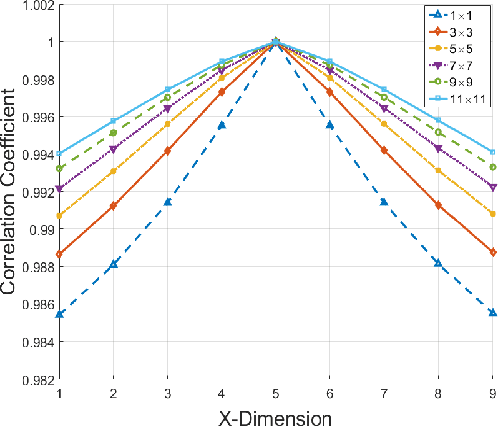
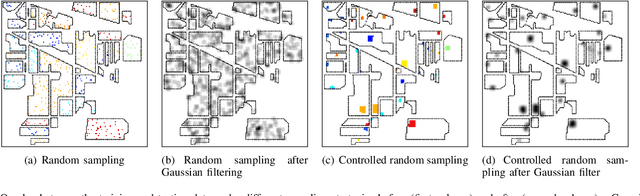
Spectral-spatial processing has been increasingly explored in remote sensing hyperspectral image classification. While extensive studies have focused on developing methods to improve the classification accuracy, experimental setting and design for method evaluation have drawn little attention. In the scope of supervised classification, we find that traditional experimental designs for spectral processing are often improperly used in the spectral-spatial processing context, leading to unfair or biased performance evaluation. This is especially the case when training and testing samples are randomly drawn from the same image - a practice that has been commonly adopted in the experiments. Under such setting, the dependence caused by overlap between the training and testing samples may be artificially enhanced by some spatial information processing methods such as spatial filtering and morphological operation. Such interaction between training and testing sets has violated data independence assumption that is abided by supervised learning theory and performance evaluation mechanism. Therefore, the widely adopted pixel-based random sampling strategy is not always suitable to evaluate spectral-spatial classification algorithms because it is difficult to determine whether the improvement of classification accuracy is caused by incorporating spatial information into classifier or by increasing the overlap between training and testing samples. To partially solve this problem, we propose a novel controlled random sampling strategy for spectral-spatial methods. It can greatly reduce the overlap between training and testing samples and provides more objective and accurate evaluation.

Preferential Multi-Context Systems

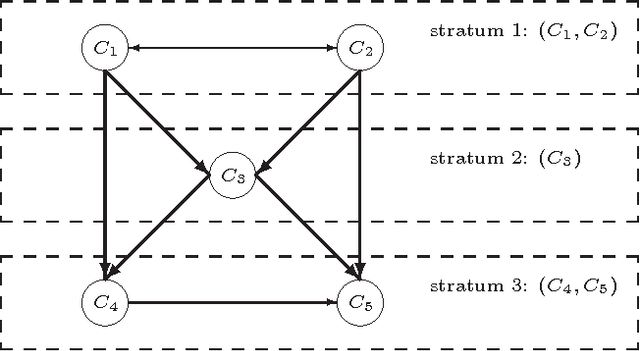
Multi-context systems (MCS) presented by Brewka and Eiter can be considered as a promising way to interlink decentralized and heterogeneous knowledge contexts. In this paper, we propose preferential multi-context systems (PMCS), which provide a framework for incorporating a total preorder relation over contexts in a multi-context system. In a given PMCS, its contexts are divided into several parts according to the total preorder relation over them, moreover, only information flows from a context to ones of the same part or less preferred parts are allowed to occur. As such, the first $l$ preferred parts of an PMCS always fully capture the information exchange between contexts of these parts, and then compose another meaningful PMCS, termed the $l$-section of that PMCS. We generalize the equilibrium semantics for an MCS to the (maximal) $l_{\leq}$-equilibrium which represents belief states at least acceptable for the $l$-section of an PMCS. We also investigate inconsistency analysis in PMCS and related computational complexity issues.

Random Logic Programs: Linear Model

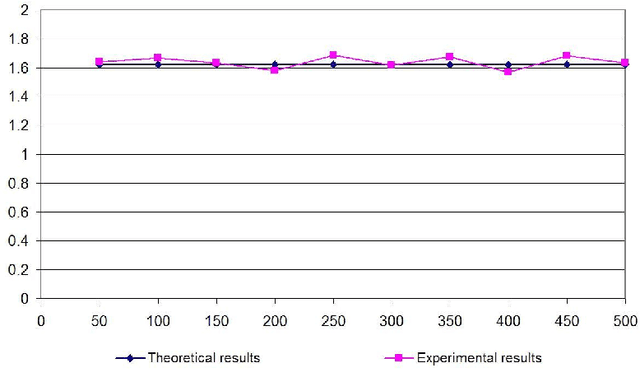
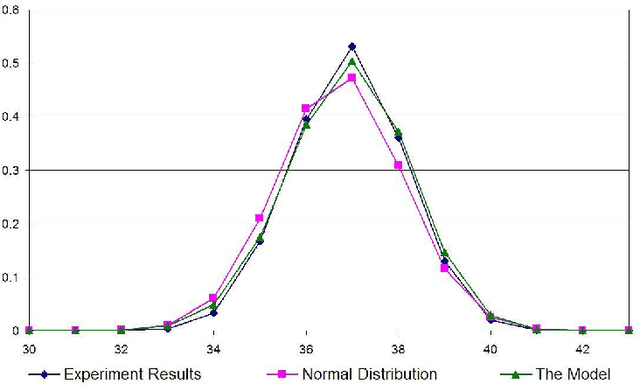
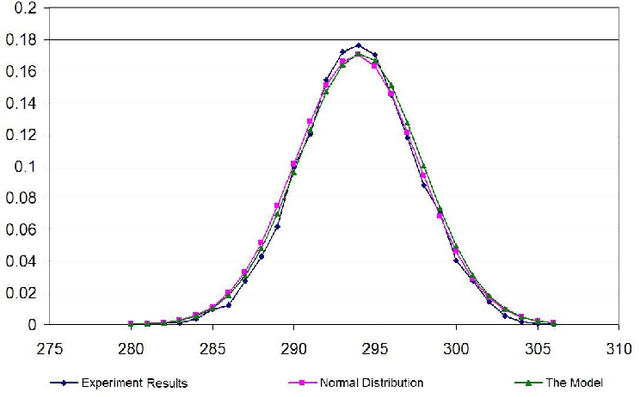
This paper proposes a model, the linear model, for randomly generating logic programs with low density of rules and investigates statistical properties of such random logic programs. It is mathematically shown that the average number of answer sets for a random program converges to a constant when the number of atoms approaches infinity. Several experimental results are also reported, which justify the suitability of the linear model. It is also experimentally shown that, under this model, the size distribution of answer sets for random programs tends to a normal distribution when the number of atoms is sufficiently large.