Preferential Multi-Context Systems
Paper and Code
Apr 25, 2015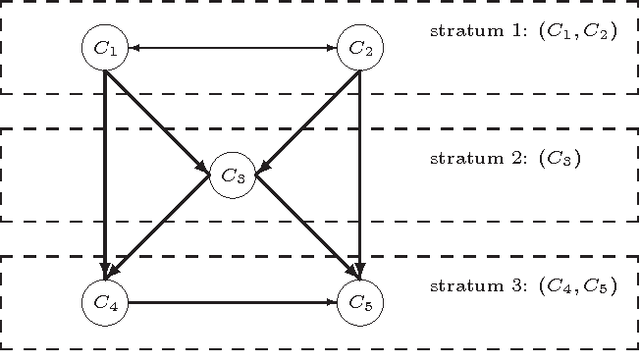

Multi-context systems (MCS) presented by Brewka and Eiter can be considered as a promising way to interlink decentralized and heterogeneous knowledge contexts. In this paper, we propose preferential multi-context systems (PMCS), which provide a framework for incorporating a total preorder relation over contexts in a multi-context system. In a given PMCS, its contexts are divided into several parts according to the total preorder relation over them, moreover, only information flows from a context to ones of the same part or less preferred parts are allowed to occur. As such, the first $l$ preferred parts of an PMCS always fully capture the information exchange between contexts of these parts, and then compose another meaningful PMCS, termed the $l$-section of that PMCS. We generalize the equilibrium semantics for an MCS to the (maximal) $l_{\leq}$-equilibrium which represents belief states at least acceptable for the $l$-section of an PMCS. We also investigate inconsistency analysis in PMCS and related computational complexity issues.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge