Syntax-Preserving Belief Change Operators for Logic Programs
Paper and Code
Mar 17, 2017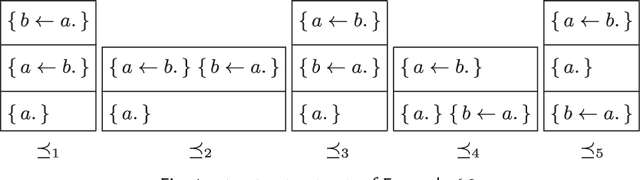
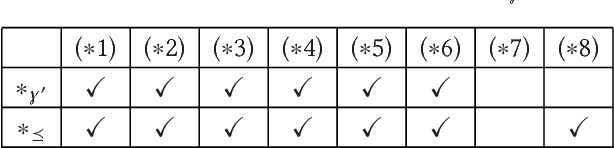
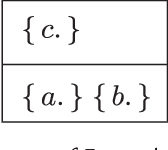

Recent methods have adapted the well-established AGM and belief base frameworks for belief change to cover belief revision in logic programs. In this study here, we present two new sets of belief change operators for logic programs. They focus on preserving the explicit relationships expressed in the rules of a program, a feature that is missing in purely semantic approaches that consider programs only in their entirety. In particular, operators of the latter class fail to satisfy preservation and support, two important properties for belief change in logic programs required to ensure intuitive results. We address this shortcoming of existing approaches by introducing partial meet and ensconcement constructions for logic program belief change, which allow us to define syntax-preserving operators that satisfy preservation and support. Our work is novel in that our constructions not only preserve more information from a logic program during a change operation than existing ones, but they also facilitate natural definitions of contraction operators, the first in the field to the best of our knowledge. In order to evaluate the rationality of our operators, we translate the revision and contraction postulates from the AGM and belief base frameworks to the logic programming setting. We show that our operators fully comply with the belief base framework and formally state the interdefinability between our operators. We further propose an algorithm that is based on modularising a logic program to reduce partial meet and ensconcement revisions or contractions to performing the operation only on the relevant modules of that program. Finally, we compare our approach to two state-of-the-art logic program revision methods and demonstrate that our operators address the shortcomings of one and generalise the other method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge