Factor-Graph-Based Passive Acoustic Navigation for Decentralized Cooperative Localization Using Bearing Elevation Depth Difference

Accurate and scalable underwater multi-agent localization remains a critical challenge due to the constraints of underwater communication. In this work, we propose a multi-agent localization framework using a factor-graph representation that incorporates bearing, elevation, and depth difference (BEDD). Our method leverages inverted ultra-short baseline (inverted-USBL) derived azimuth and elevation measurements from incoming acoustic signals and relative depth measurements to enable cooperative localization for a multi-robot team of autonomous underwater vehicles (AUVs). We validate our approach in the HoloOcean underwater simulator with a fleet of AUVs, demonstrating improved localization accuracy compared to dead reckoning. Additionally, we investigate the impact of azimuth and elevation measurement outliers, highlighting the need for robust outlier rejection techniques for acoustic signals.

Invariant Extended Kalman Filter for Autonomous Surface Vessels with Partial Orientation Measurements

Autonomous surface vessels (ASVs) are increasingly vital for marine science, offering robust platforms for underwater mapping and inspection. Accurate state estimation, particularly of vehicle pose, is paramount for precise seafloor mapping, as even small surface deviations can have significant consequences when sensing the seafloor below. To address this challenge, we propose an Invariant Extended Kalman Filter (InEKF) framework designed to integrate partial orientation measurements. While conventional estimation often relies on relative position measurements to fixed landmarks, open ocean ASVs primarily observe a receding horizon. We leverage forward-facing monocular cameras to estimate roll and pitch with respect to this horizon, which provides yaw-ambiguous partial orientation information. To effectively utilize these measurements within the InEKF, we introduce a novel framework for incorporating such partial orientation data. This approach contrasts with traditional InEKF implementations that assume full orientation measurements and is particularly relevant for planar vehicle motion constrained to a "seafaring plane." This paper details the developed InEKF framework; its integration with horizon-based roll/pitch observations and dual-antenna GPS heading measurements for ASV state estimation; and provides a comparative analysis against the InEKF using full orientation and a Multiplicative EKF (MEKF). Our results demonstrate the efficacy and robustness of the proposed partial orientation measurements for accurate ASV state estimation in open ocean environments.

Group-$k$ consistent measurement set maximization via maximum clique over k-Uniform hypergraphs for robust multi-robot map merging

This paper unifies the theory of consistent-set maximization for robust outlier detection in a simultaneous localization and mapping framework. We first describe the notion of pairwise consistency before discussing how a consistency graph can be formed by evaluating pairs of measurements for consistency. Finding the largest set of consistent measurements is transformed into an instance of the maximum clique problem and can be solved relatively quickly using existing maximum-clique solvers. We then generalize our algorithm to check consistency on a group-$k$ basis by using a generalized notion of consistency and using generalized graphs. We also present modified maximum clique algorithms that function on generalized graphs to find the set of measurements that is internally group-$k$ consistent. We address the exponential nature of group-$k$ consistency and present methods that can substantially decrease the number of necessary checks performed when evaluating consistency. We extend our prior work to multi-agent systems in both simulation and hardware and provide a comparison with other state-of-the-art methods.

Group-$k$ Consistent Measurement Set Maximization for Robust Outlier Detection

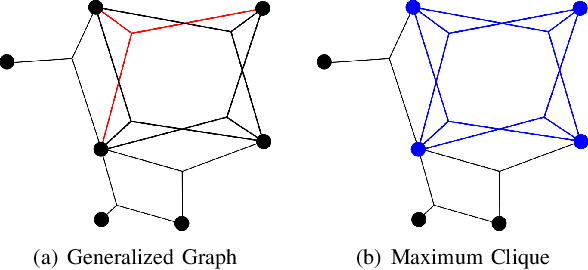
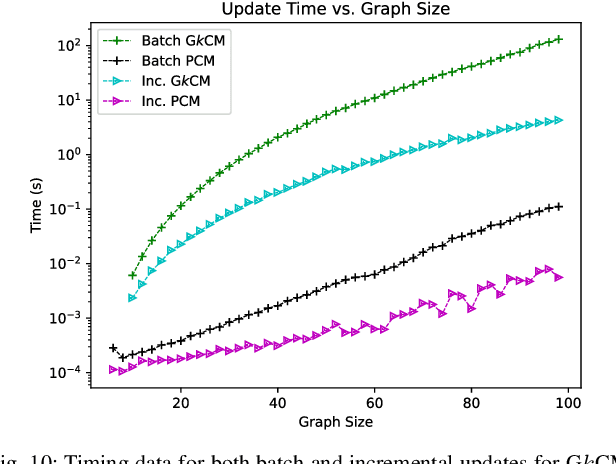
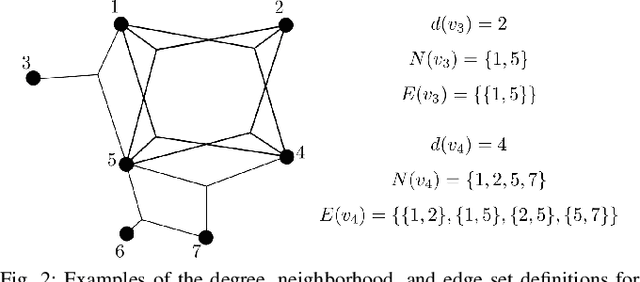
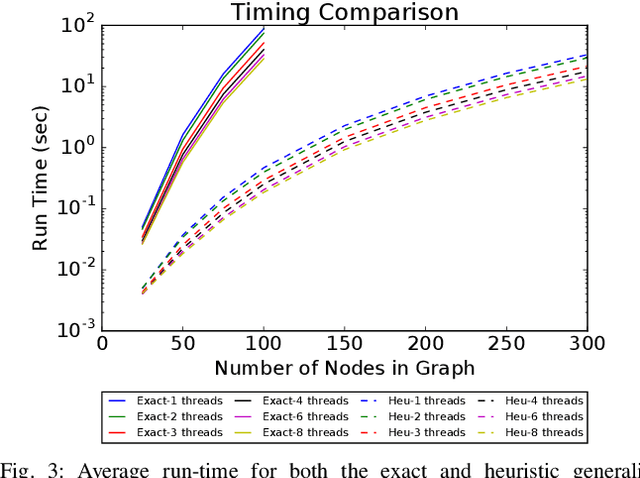
This paper presents a method for the robust selection of measurements in a simultaneous localization and mapping (SLAM) framework. Existing methods check consistency or compatibility on a pairwise basis, however many measurement types are not sufficiently constrained in a pairwise scenario to determine if either measurement is inconsistent with the other. This paper presents group-$k$ consistency maximization (G$k$CM) that estimates the largest set of measurements that is internally group-$k$ consistent. Solving for the largest set of group-$k$ consistent measurements can be formulated as an instance of the maximum clique problem on generalized graphs and can be solved by adapting current methods. This paper evaluates the performance of G$k$CM using simulated data and compares it to pairwise consistency maximization (PCM) presented in previous work.

Efficient shape mapping through dense touch and vision

Knowledge of 3-D object shape is of great importance to robot manipulation tasks, but may not be readily available in unstructured environments. While vision is often occluded during robot-object interaction, high-resolution tactile sensors can give a dense local perspective of the object. However, tactile sensors have limited sensing area and the shape representation must faithfully approximate non-contact areas. In addition, a key challenge is efficiently incorporating these dense tactile measurements into a 3-D mapping framework. In this work, we propose an incremental shape mapping method using a GelSight tactile sensor and a depth camera. Local shape is recovered from tactile images via a learned model trained in simulation. Through efficient inference on a spatial factor graph informed by a Gaussian process, we build an implicit surface representation of the object. We demonstrate visuo-tactile mapping in both simulated and real-world experiments, to incrementally build 3-D reconstructions of household objects.

Tactile SLAM: Real-time inference of shape and pose from planar pushing

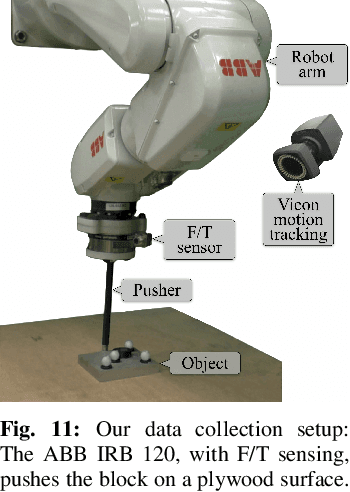
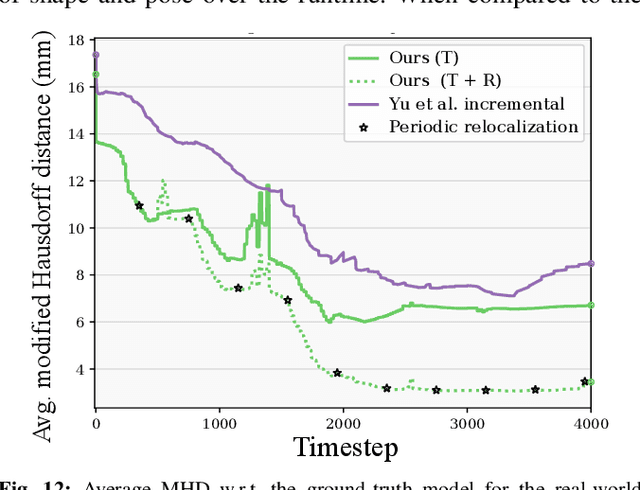
Tactile perception is central to robot manipulation in unstructured environments. However, it requires contact, and a mature implementation must infer object models while also accounting for the motion induced by the interaction. In this work, we present a method to estimate both object shape and pose in real-time from a stream of tactile measurements. This is applied towards tactile exploration of an unknown object by planar pushing. We consider this as an online SLAM problem with a nonparametric shape representation. Our formulation of tactile inference alternates between Gaussian process implicit surface regression and pose estimation on a factor graph. Through a combination of local Gaussian processes and fixed-lag smoothing, we infer object shape and pose in real-time. We evaluate our system across different objects in both simulated and real-world planar pushing tasks.

Characterizing the Uncertainty of Jointly Distributed Poses in the Lie Algebra

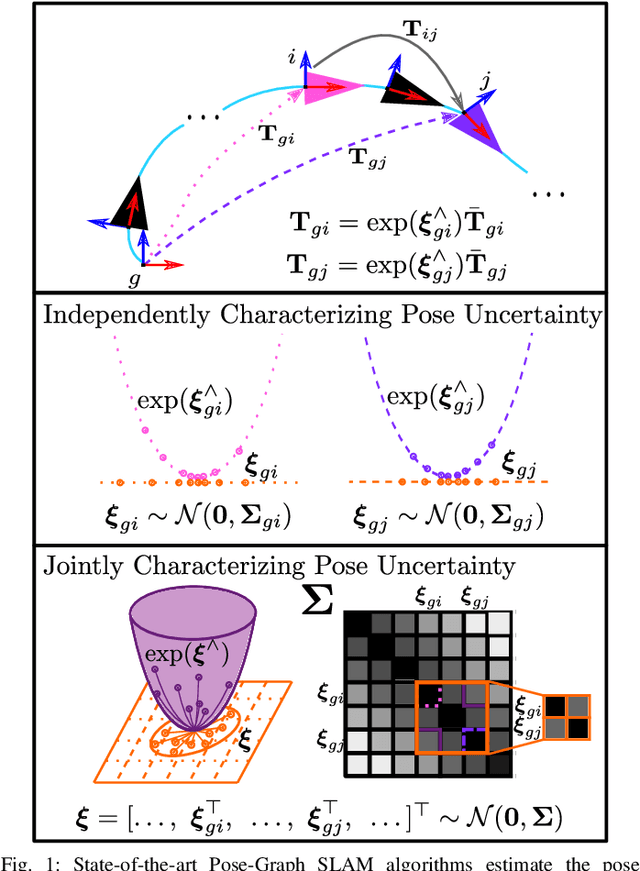
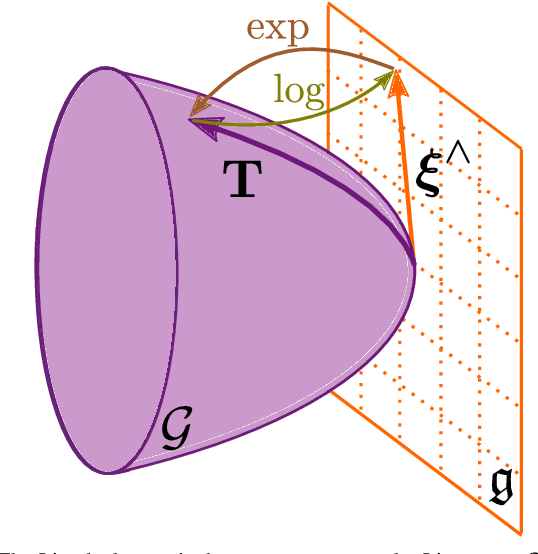
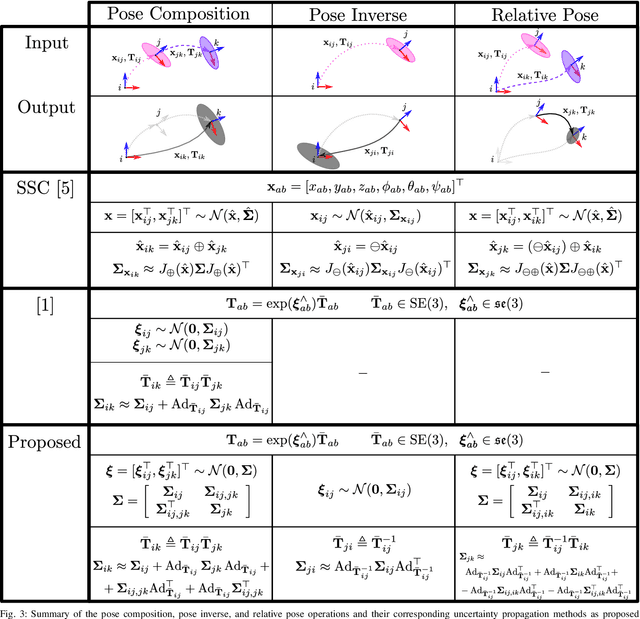
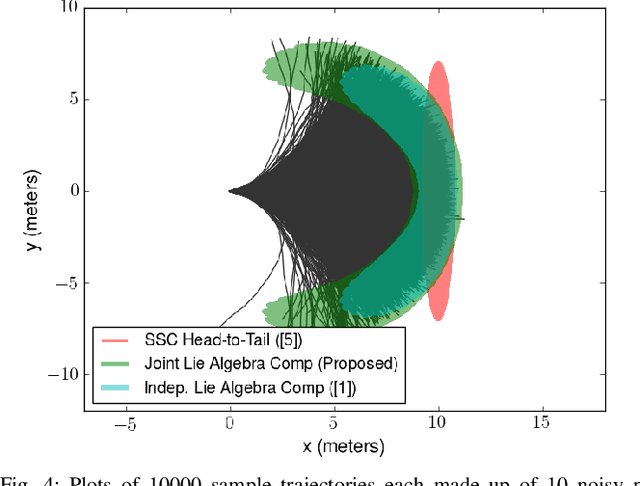
An accurate characterization of pose uncertainty is essential for safe autonomous navigation. Early pose uncertainty characterization methods proposed by Smith, Self, and Cheeseman (SCC), used coordinate-based first-order methods to propagate uncertainty through non-linear functions such as pose composition (head-to-tail), pose inversion, and relative pose extraction (tail-to-tail). Characterizing uncertainty in the Lie Algebra of the special Euclidean group results in better uncertainty estimates. However, existing approaches assume that individual poses are independent. Since factors in a pose graph induce correlation, this independence assumption is usually not reflected in reality. In addition, prior work has focused primarily on the pose composition operation. This paper develops a framework for modeling the uncertainty of jointly distributed poses and describes how to perform the equivalent of the SSC pose operations while characterizing uncertainty in the Lie Algebra. Evaluation on simulated and open-source datasets shows that the proposed methods result in more accurate uncertainty estimates. An accompanying C++ library implementation is also released. This is a pre-print of a paper submitted to IEEE TRO in 2019.

Guaranteed Globally Optimal Planar Pose Graph and Landmark SLAM via Sparse-Bounded Sums-of-Squares Programming

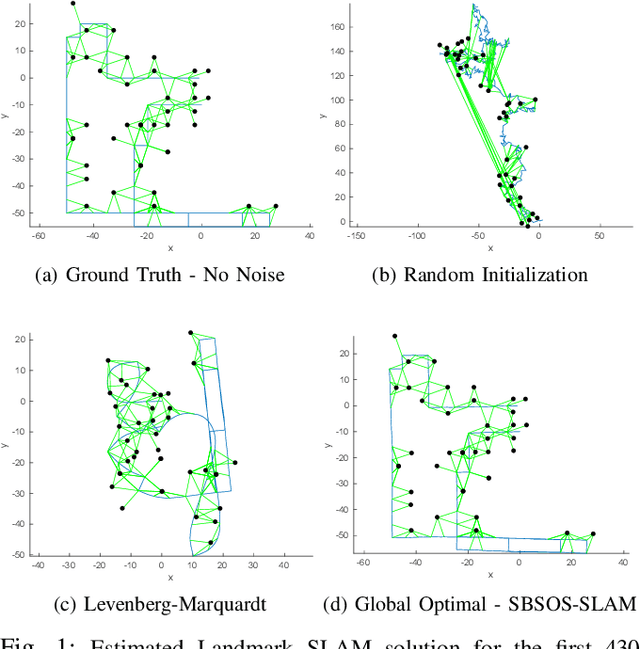
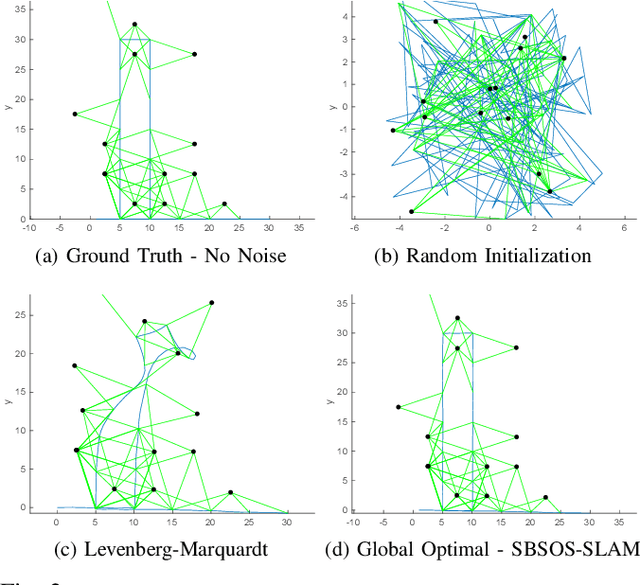
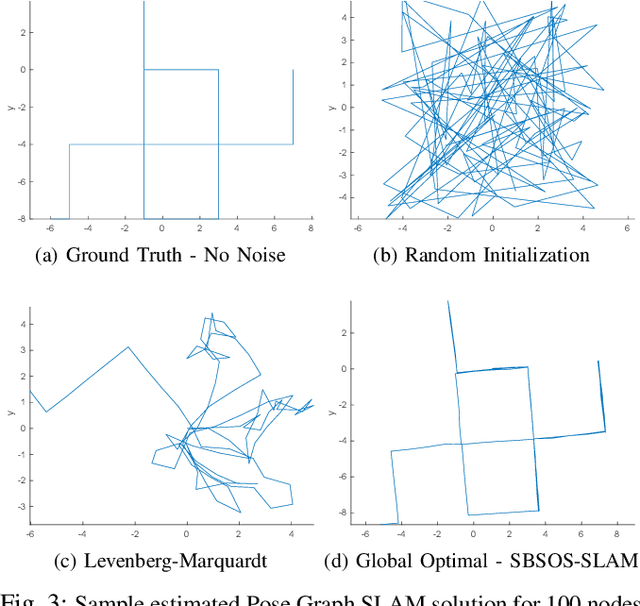
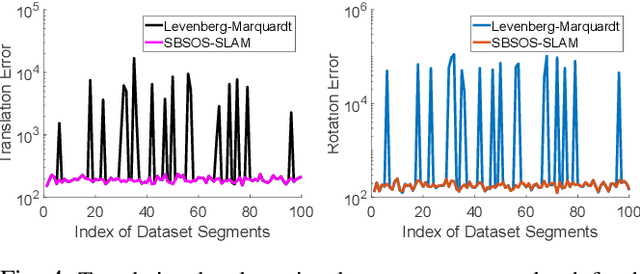
Autonomous navigation requires an accurate model or map of the environment. While dramatic progress in the prior two decades has enabled large-scale simultaneous localization and mapping (SLAM), the majority of existing methods rely on non-linear optimization techniques to find the maximum likelihood estimate (MLE) of the robot trajectory and surrounding environment. These methods are prone to local minima and are thus sensitive to initialization. Several recent papers have developed optimization algorithms for the Pose-Graph SLAM problem that can certify the optimality of a computed solution. Though this does not guarantee a priori that this approach generates an optimal solution, a recent extension has shown that when the noise lies within a critical threshold that the solution to the optimization algorithm is guaranteed to be optimal. To address the limitations of existing approaches, this paper illustrates that the Pose-Graph SLAM and Landmark SLAM can be formulated as polynomial optimization programs that are sum-of-squares (SOS) convex. This paper then describes how the Pose-Graph and Landmark SLAM problems can be solved to a global minimum without initialization regardless of noise level using the sparse bounded degree sum-of-squares (Sparse-BSOS) optimization method. Finally, the superior performance of the proposed approach when compared to existing SLAM methods is illustrated on graphs with several hundred nodes.