Characterizing the Uncertainty of Jointly Distributed Poses in the Lie Algebra
Paper and Code
Jun 18, 2019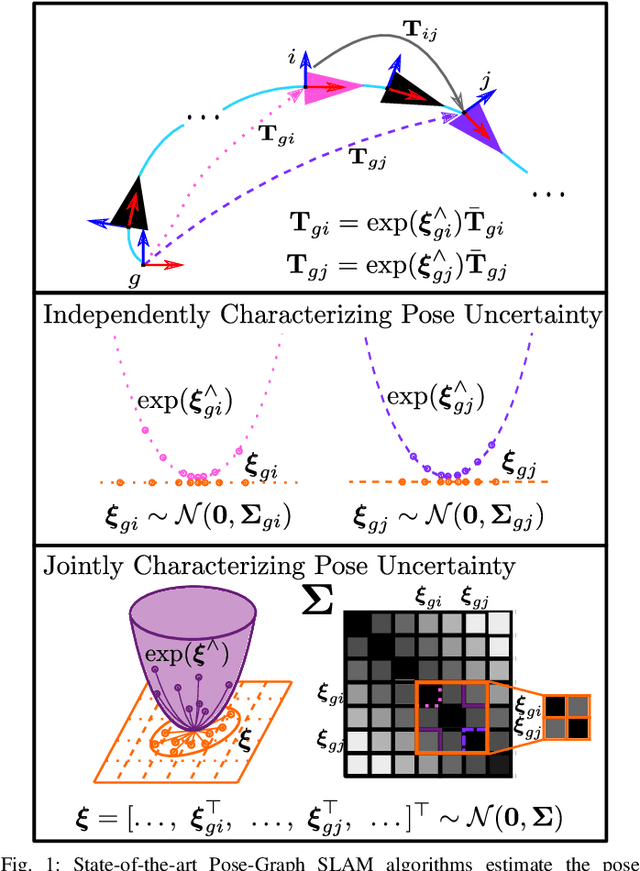
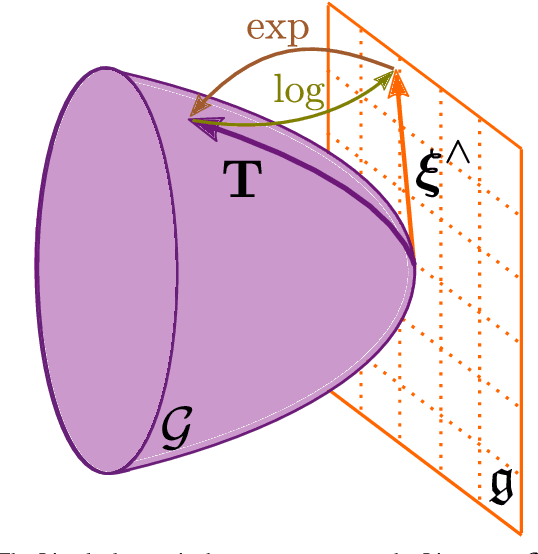
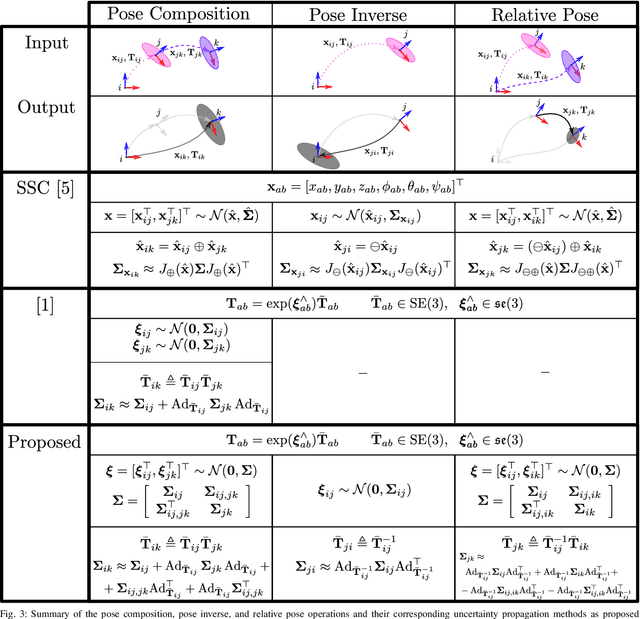
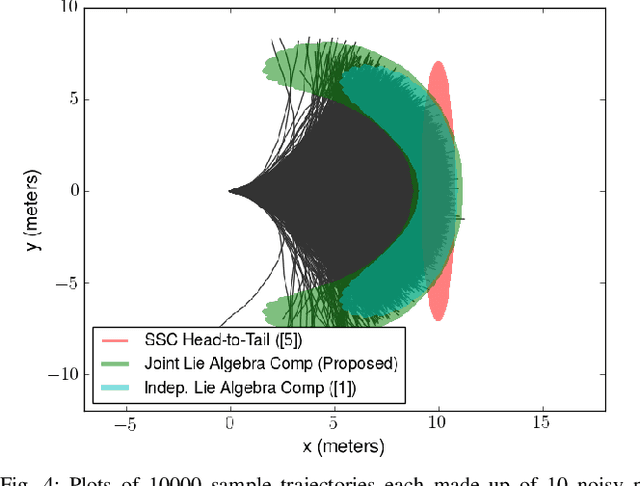
An accurate characterization of pose uncertainty is essential for safe autonomous navigation. Early pose uncertainty characterization methods proposed by Smith, Self, and Cheeseman (SCC), used coordinate-based first-order methods to propagate uncertainty through non-linear functions such as pose composition (head-to-tail), pose inversion, and relative pose extraction (tail-to-tail). Characterizing uncertainty in the Lie Algebra of the special Euclidean group results in better uncertainty estimates. However, existing approaches assume that individual poses are independent. Since factors in a pose graph induce correlation, this independence assumption is usually not reflected in reality. In addition, prior work has focused primarily on the pose composition operation. This paper develops a framework for modeling the uncertainty of jointly distributed poses and describes how to perform the equivalent of the SSC pose operations while characterizing uncertainty in the Lie Algebra. Evaluation on simulated and open-source datasets shows that the proposed methods result in more accurate uncertainty estimates. An accompanying C++ library implementation is also released. This is a pre-print of a paper submitted to IEEE TRO in 2019.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge