Group-$k$ consistent measurement set maximization via maximum clique over k-Uniform hypergraphs for robust multi-robot map merging

This paper unifies the theory of consistent-set maximization for robust outlier detection in a simultaneous localization and mapping framework. We first describe the notion of pairwise consistency before discussing how a consistency graph can be formed by evaluating pairs of measurements for consistency. Finding the largest set of consistent measurements is transformed into an instance of the maximum clique problem and can be solved relatively quickly using existing maximum-clique solvers. We then generalize our algorithm to check consistency on a group-$k$ basis by using a generalized notion of consistency and using generalized graphs. We also present modified maximum clique algorithms that function on generalized graphs to find the set of measurements that is internally group-$k$ consistent. We address the exponential nature of group-$k$ consistency and present methods that can substantially decrease the number of necessary checks performed when evaluating consistency. We extend our prior work to multi-agent systems in both simulation and hardware and provide a comparison with other state-of-the-art methods.

Incremental cycle bases for cycle-based pose graph optimization

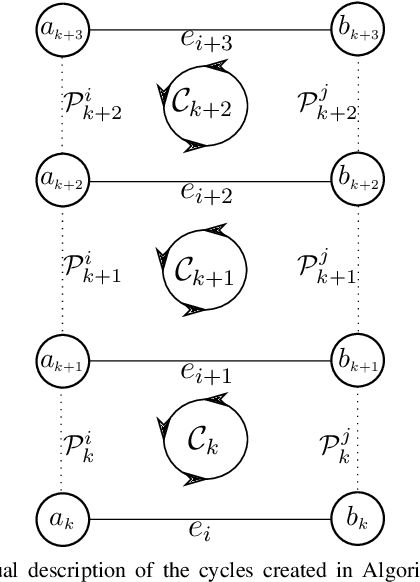
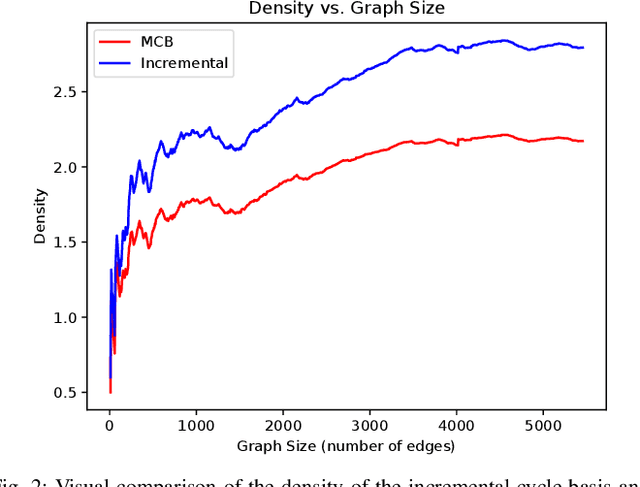
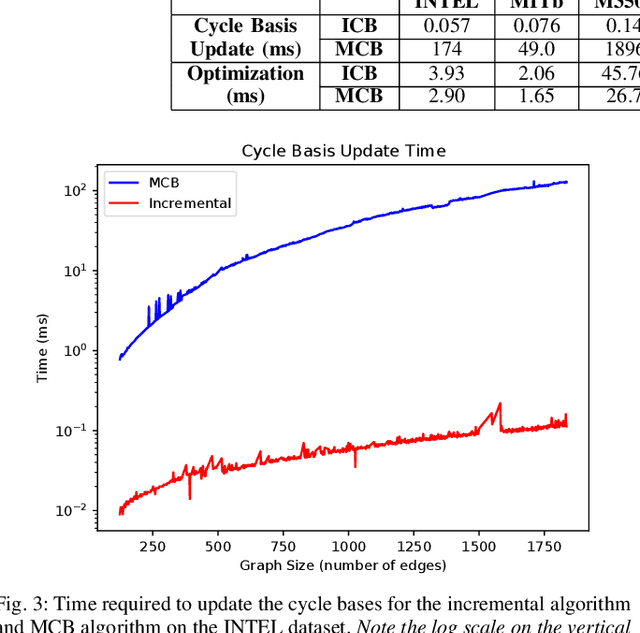
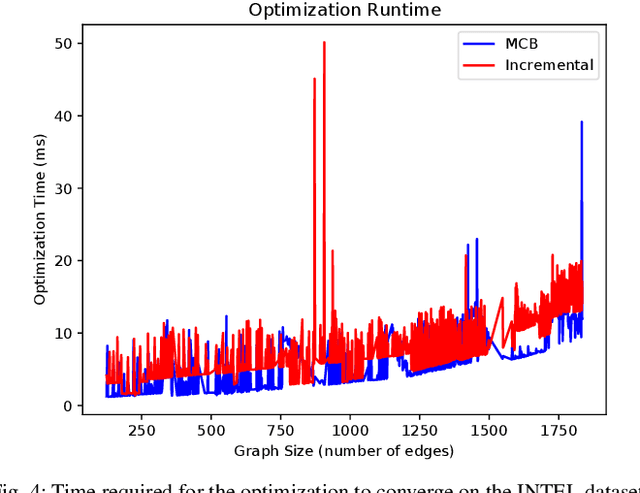
Pose graph optimization is a special case of the simultaneous localization and mapping problem where the only variables to be estimated are pose variables and the only measurements are inter-pose constraints. The vast majority of PGO techniques are vertex based (variables are robot poses), but recent work has parameterized the pose graph optimization problem in a relative fashion (variables are the transformations between poses) that utilizes a minimum cycle basis to maximize the sparsity of the problem. We explore the construction of a cycle basis in an incremental manner while maximizing the sparsity. We validate an algorithm that constructs a sparse cycle basis incrementally and compare its performance with a minimum cycle basis. Additionally, we present an algorithm to approximate the minimum cycle basis of two graphs that are sparsely connected as is common in multi-agent scenarios. Lastly, the relative parameterization of pose graph optimization has been limited to using rigid body transforms on SE(2) or SE(3) as the constraints between poses. We introduce a methodology to allow for the use of lower-degree-of-freedom measurements in the relative pose graph optimization problem. We provide extensive validation of our algorithms on standard benchmarks, simulated datasets, and custom hardware.

Group-$k$ Consistent Measurement Set Maximization for Robust Outlier Detection

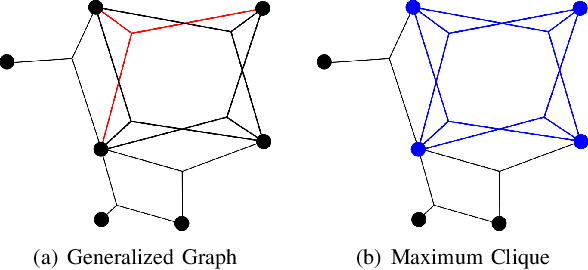
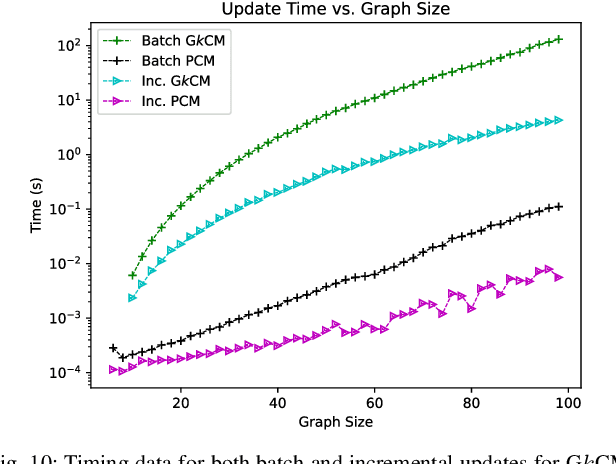
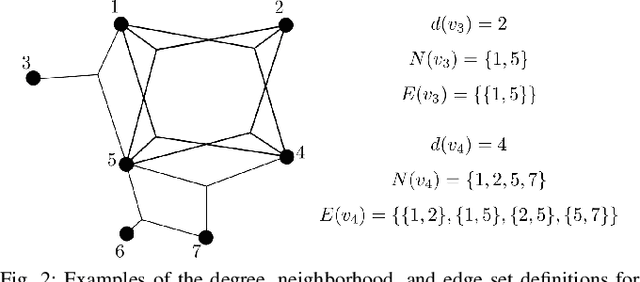
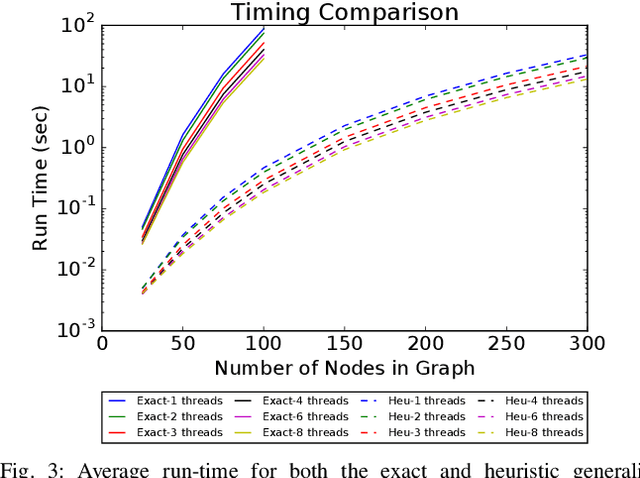
This paper presents a method for the robust selection of measurements in a simultaneous localization and mapping (SLAM) framework. Existing methods check consistency or compatibility on a pairwise basis, however many measurement types are not sufficiently constrained in a pairwise scenario to determine if either measurement is inconsistent with the other. This paper presents group-$k$ consistency maximization (G$k$CM) that estimates the largest set of measurements that is internally group-$k$ consistent. Solving for the largest set of group-$k$ consistent measurements can be formulated as an instance of the maximum clique problem on generalized graphs and can be solved by adapting current methods. This paper evaluates the performance of G$k$CM using simulated data and compares it to pairwise consistency maximization (PCM) presented in previous work.