Group-$k$ Consistent Measurement Set Maximization for Robust Outlier Detection
Paper and Code
Sep 06, 2022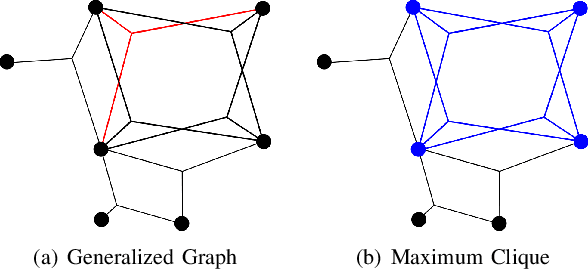
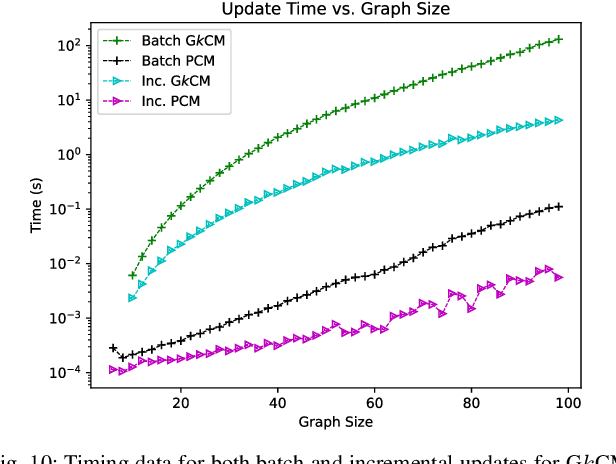
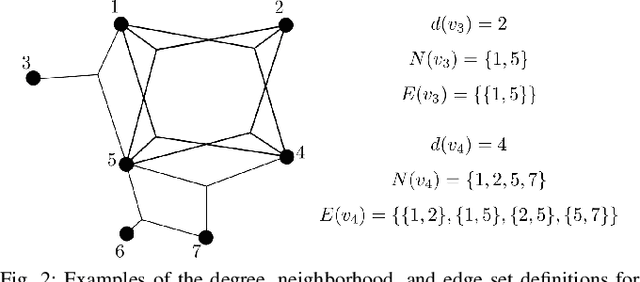
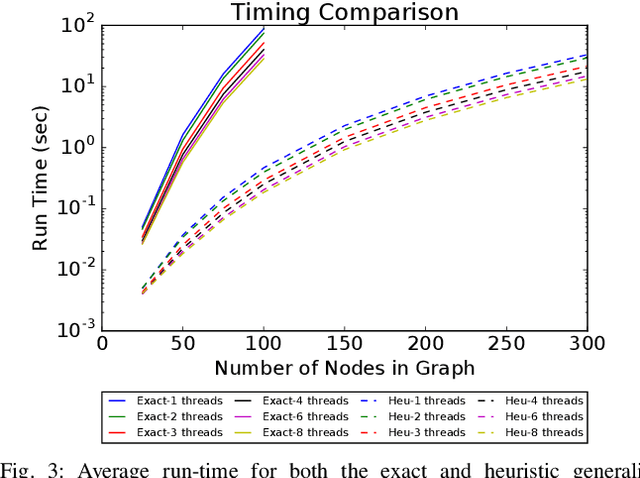
This paper presents a method for the robust selection of measurements in a simultaneous localization and mapping (SLAM) framework. Existing methods check consistency or compatibility on a pairwise basis, however many measurement types are not sufficiently constrained in a pairwise scenario to determine if either measurement is inconsistent with the other. This paper presents group-$k$ consistency maximization (G$k$CM) that estimates the largest set of measurements that is internally group-$k$ consistent. Solving for the largest set of group-$k$ consistent measurements can be formulated as an instance of the maximum clique problem on generalized graphs and can be solved by adapting current methods. This paper evaluates the performance of G$k$CM using simulated data and compares it to pairwise consistency maximization (PCM) presented in previous work.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge