Reachability-based Trajectory Design via Exact Formulation of Implicit Neural Signed Distance Functions

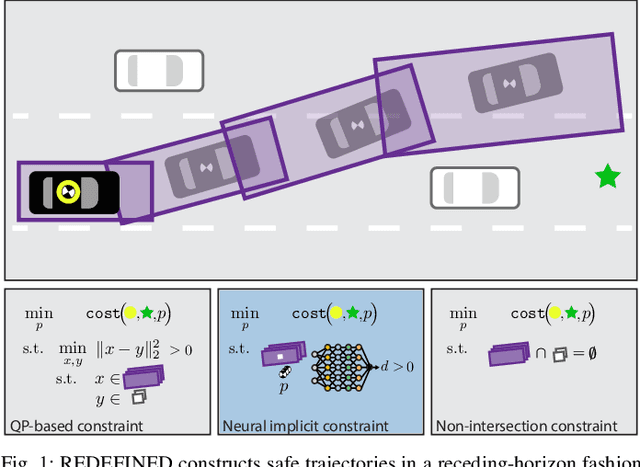
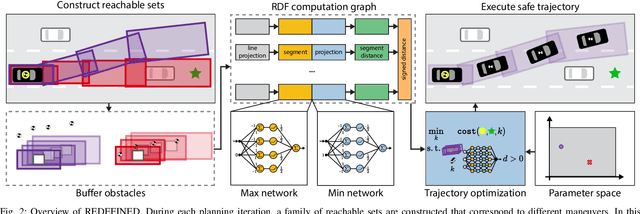
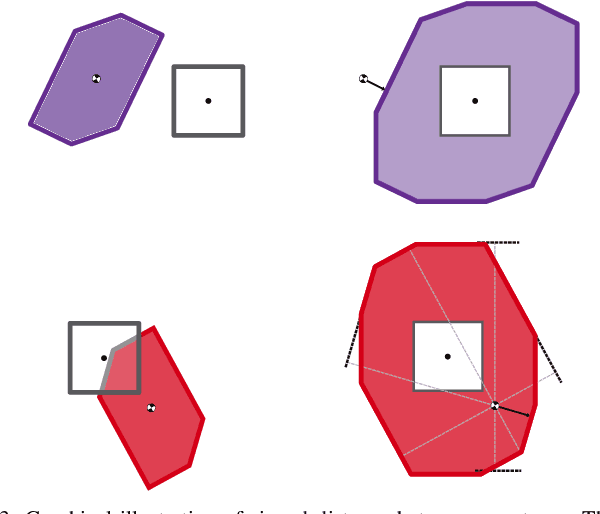
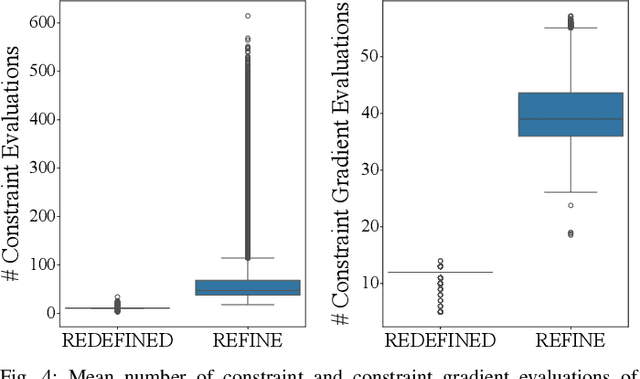
Generating receding-horizon motion trajectories for autonomous vehicles in real-time while also providing safety guarantees is challenging. This is because a future trajectory needs to be planned before the previously computed trajectory is completely executed. This becomes even more difficult if the trajectory is required to satisfy continuous-time collision-avoidance constraints while accounting for a large number of obstacles. To address these challenges, this paper proposes a novel real-time, receding-horizon motion planning algorithm named REachability-based trajectory Design via Exact Formulation of Implicit NEural signed Distance functions (REDEFINED). REDEFINED first applies offline reachability analysis to compute zonotope-based reachable sets that overapproximate the motion of the ego vehicle. During online planning, REDEFINED leverages zonotope arithmetic to construct a neural implicit representation that computes the exact signed distance between a parameterized swept volume of the ego vehicle and obstacle vehicles. REDEFINED then implements a novel, real-time optimization framework that utilizes the neural network to construct a collision avoidance constraint. REDEFINED is compared to a variety of state-of-the-art techniques and is demonstrated to successfully enable the vehicle to safely navigate through complex environments. Code, data, and video demonstrations can be found at https://roahmlab.github.io/redefined/.

Not All Actions Are Created Equal: Bayesian Optimal Experimental Design for Safe and Optimal Nonlinear System Identification

Uncertainty in state or model parameters is common in robotics and typically handled by acquiring system measurements that yield information about the uncertain quantities of interest. Inputs to a nonlinear dynamical system yield outcomes that produce varying amounts of information about the underlying uncertain parameters of the system. To maximize information gained with respect to these uncertain parameters we present a Bayesian approach to data collection for system identification called Bayesian Optimal Experimental Design (BOED). The formulation uses parameterized trajectories and cubature to compute maximally informative system trajectories which obtain as much information as possible about unknown system parameters while also ensuring safety under mild assumptions. The proposed method is applicable to non-linear and non-Gaussian systems and is applied to a high-fidelity vehicle model from the literature. It is shown the proposed approach requires orders of magnitude fewer samples compared to state-of-the-art BOED algorithms from the literature while simultaneously providing safety guarantees.

RADIUS: Risk-Aware, Real-Time, Reachability-Based Motion Planning

Deterministic methods for motion planning guarantee safety amidst uncertainty in obstacle locations by trying to restrict the robot from operating in any possible location that an obstacle could be in. Unfortunately, this can result in overly conservative behavior. Chance-constrained optimization can be applied to improve the performance of motion planning algorithms by allowing for a user-specified amount of bounded constraint violation. However, state-of-the-art methods rely either on moment-based inequalities, which can be overly conservative, or make it difficult to satisfy assumptions about the class of probability distributions used to model uncertainty. To address these challenges, this work proposes a real-time, risk-aware reachability based motion planning framework called RADIUS. The method first generates a reachable set of parameterized trajectories for the robot offline. At run time, RADIUS computes a closed-form over-approximation of the risk of a collision with an obstacle. This is done without restricting the probability distribution used to model uncertainty to a simple class (e.g., Gaussian). Then, RADIUS performs real-time optimization to construct a trajectory that can be followed by the robot in a manner that is certified to have a risk of collision that is less than or equal to a user-specified threshold. The proposed algorithm is compared to several state-of-the-art chance-constrained and deterministic methods in simulation, and is shown to consistently outperform them in a variety of driving scenarios. A demonstration of the proposed framework on hardware is also provided.

REFINE: Reachability-based Trajectory Design using Robust Feedback Linearization and Zonotopes

Performing real-time receding horizon motion planning for autonomous vehicles while providing safety guarantees remains difficult. This is because existing methods to accurately predict ego vehicle behavior under a chosen controller use online numerical integration that requires a fine time discretization and thereby adversely affects real-time performance. To address this limitation, several recent papers have proposed to apply offline reachability analysis to conservatively predict the behavior of the ego vehicle. This reachable set can be constructed by utilizing a simplified model whose behavior is assumed a priori to conservatively bound the dynamics of a full-order model. However, guaranteeing that one satisfies this assumption is challenging. This paper proposes a framework named REFINE to overcome the limitations of these existing approaches. REFINE utilizes a parameterized robust controller that partially linearizes the vehicle dynamics even in the presence of modeling error. Zonotope-based reachability analysis is then performed on the closed-loop, full-order vehicle dynamics to compute the corresponding control-parameterized, over-approximate Forward Reachable Sets (FRS). Because reachability analysis is applied to the full-order model, the potential conservativeness introduced by using a simplified model is avoided. The pre-computed, control-parameterized FRS is then used online in an optimization framework to ensure safety. The proposed method is compared to several state of the art methods during a simulation-based evaluation on a full-size vehicle model and is evaluated on a 1/10th race car robot in real hardware testing. In contrast to existing methods, REFINE is shown to enable the vehicle to safely navigate itself through complex environments.

Leveraging the Template and Anchor Framework for Safe, Online Robotic Gait Design

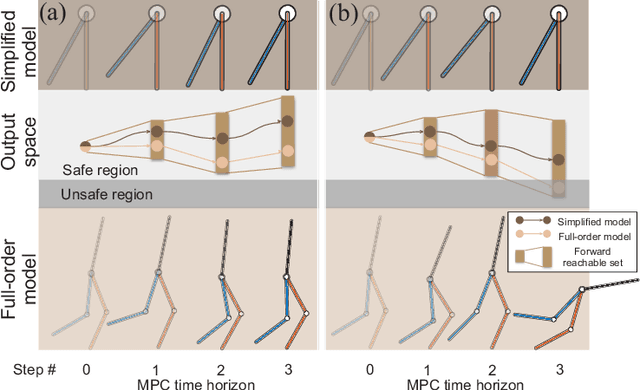
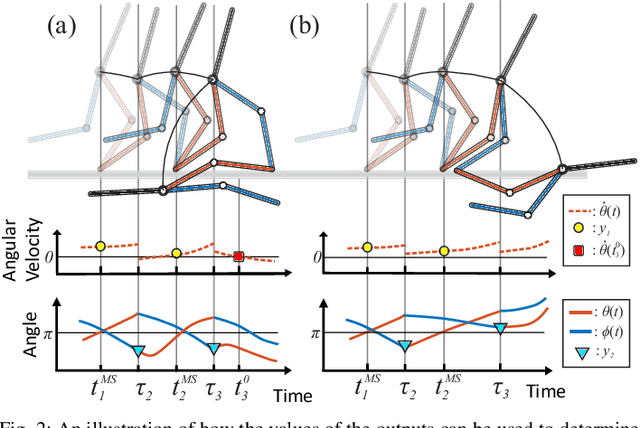
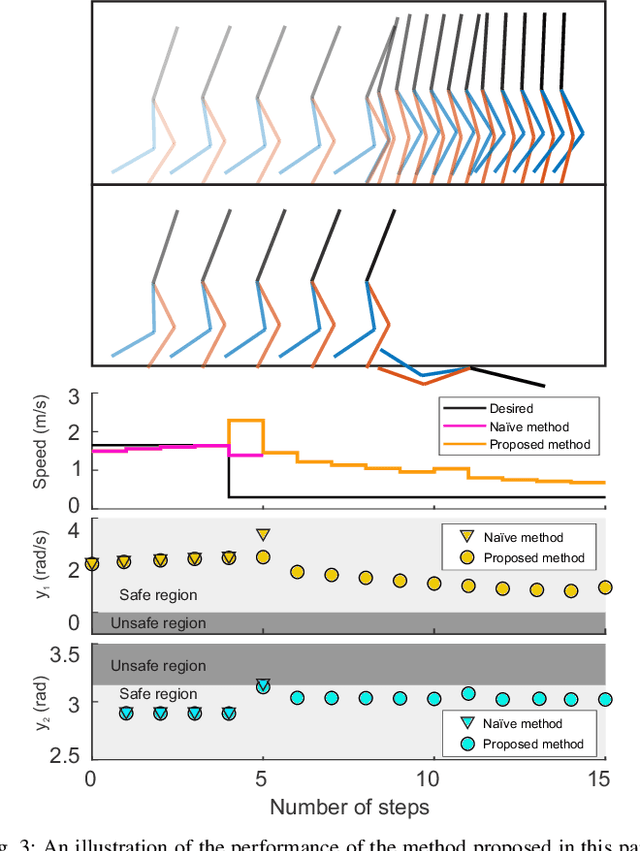
Online control design using a high-fidelity, full-order model for a bipedal robot can be challenging due to the size of the state space of the model. A commonly adopted solution to overcome this challenge is to approximate the full-order model (anchor) with a simplified, reduced-order model (template), while performing control synthesis. Unfortunately it is challenging to make formal guarantees about the safety of an anchor model using a controller designed in an online fashion using a template model. To address this problem, this paper proposes a method to generate safety-preserving controllers for anchor models by performing reachability analysis on template models while bounding the modeling error. This paper describes how this reachable set can be incorporated into a Model Predictive Control framework to select controllers that result in safe walking on the anchor model in an online fashion. The method is illustrated on a 5-link RABBIT model, and is shown to allow the robot to walk safely while utilizing controllers designed in an online fashion.

Guaranteed Globally Optimal Planar Pose Graph and Landmark SLAM via Sparse-Bounded Sums-of-Squares Programming

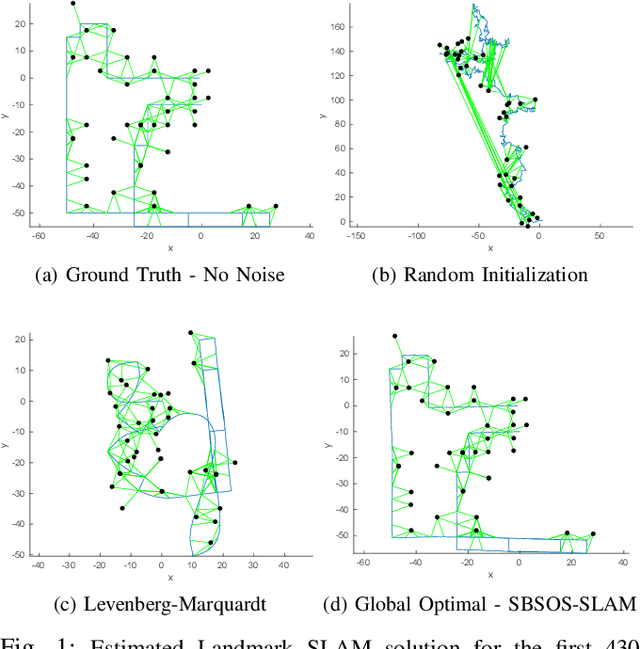
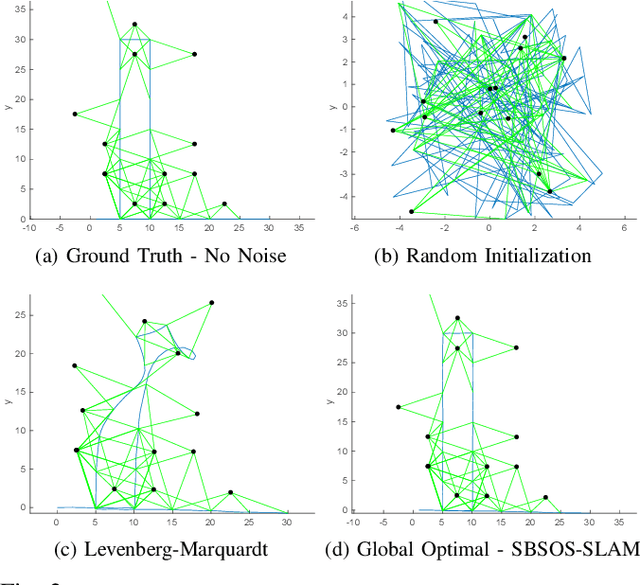
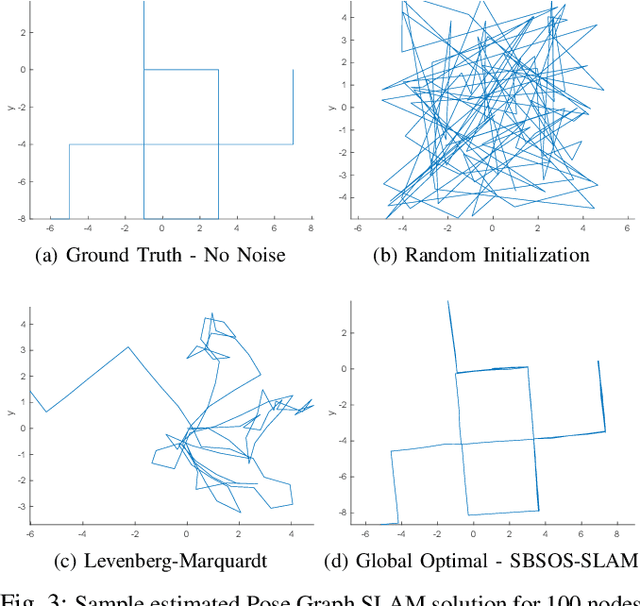
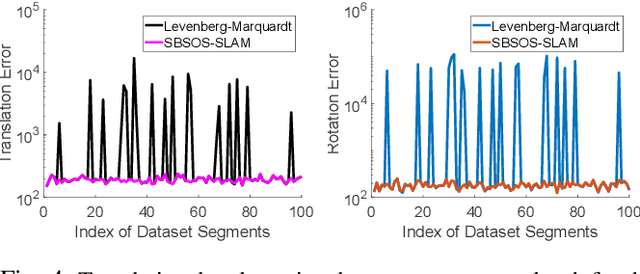
Autonomous navigation requires an accurate model or map of the environment. While dramatic progress in the prior two decades has enabled large-scale simultaneous localization and mapping (SLAM), the majority of existing methods rely on non-linear optimization techniques to find the maximum likelihood estimate (MLE) of the robot trajectory and surrounding environment. These methods are prone to local minima and are thus sensitive to initialization. Several recent papers have developed optimization algorithms for the Pose-Graph SLAM problem that can certify the optimality of a computed solution. Though this does not guarantee a priori that this approach generates an optimal solution, a recent extension has shown that when the noise lies within a critical threshold that the solution to the optimization algorithm is guaranteed to be optimal. To address the limitations of existing approaches, this paper illustrates that the Pose-Graph SLAM and Landmark SLAM can be formulated as polynomial optimization programs that are sum-of-squares (SOS) convex. This paper then describes how the Pose-Graph and Landmark SLAM problems can be solved to a global minimum without initialization regardless of noise level using the sparse bounded degree sum-of-squares (Sparse-BSOS) optimization method. Finally, the superior performance of the proposed approach when compared to existing SLAM methods is illustrated on graphs with several hundred nodes.