Gitesh Gunjal
You've Got to Feel It To Believe It: Multi-Modal Bayesian Inference for Semantic and Property Prediction
Feb 15, 2024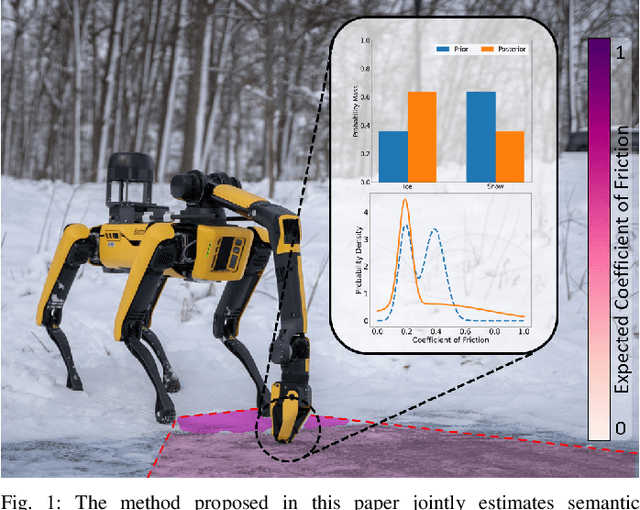
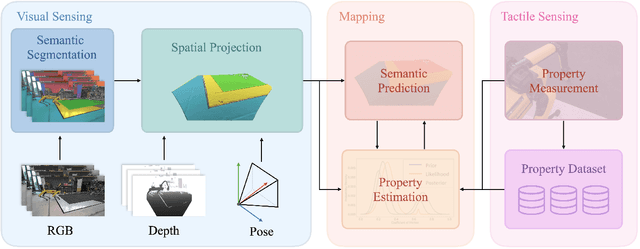
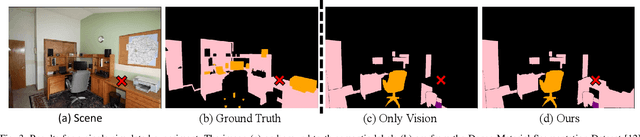
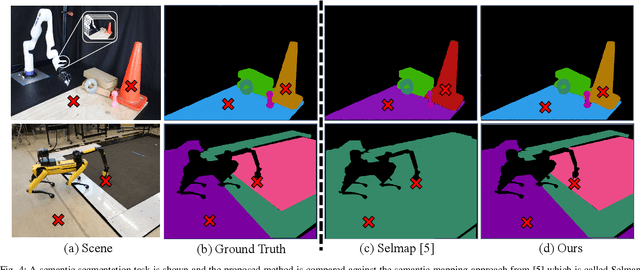
Abstract:Robots must be able to understand their surroundings to perform complex tasks in challenging environments and many of these complex tasks require estimates of physical properties such as friction or weight. Estimating such properties using learning is challenging due to the large amounts of labelled data required for training and the difficulty of updating these learned models online at run time. To overcome these challenges, this paper introduces a novel, multi-modal approach for representing semantic predictions and physical property estimates jointly in a probabilistic manner. By using conjugate pairs, the proposed method enables closed-form Bayesian updates given visual and tactile measurements without requiring additional training data. The efficacy of the proposed algorithm is demonstrated through several hardware experiments. In particular, this paper illustrates that by conditioning semantic classifications on physical properties, the proposed method quantitatively outperforms state-of-the-art semantic classification methods that rely on vision alone. To further illustrate its utility, the proposed method is used in several applications including to represent affordance-based properties probabilistically and a challenging terrain traversal task using a legged robot. In the latter task, the proposed method represents the coefficient of friction of the terrain probabilistically, which enables the use of an on-line risk-aware planner that switches the legged robot from a dynamic gait to a static, stable gait when the expected value of the coefficient of friction falls below a given threshold. Videos of these case studies as well as the open-source C++ and ROS interface can be found at https://roahmlab.github.io/multimodal_mapping/.
Not All Actions Are Created Equal: Bayesian Optimal Experimental Design for Safe and Optimal Nonlinear System Identification
Aug 03, 2023Abstract:Uncertainty in state or model parameters is common in robotics and typically handled by acquiring system measurements that yield information about the uncertain quantities of interest. Inputs to a nonlinear dynamical system yield outcomes that produce varying amounts of information about the underlying uncertain parameters of the system. To maximize information gained with respect to these uncertain parameters we present a Bayesian approach to data collection for system identification called Bayesian Optimal Experimental Design (BOED). The formulation uses parameterized trajectories and cubature to compute maximally informative system trajectories which obtain as much information as possible about unknown system parameters while also ensuring safety under mild assumptions. The proposed method is applicable to non-linear and non-Gaussian systems and is applied to a high-fidelity vehicle model from the literature. It is shown the proposed approach requires orders of magnitude fewer samples compared to state-of-the-art BOED algorithms from the literature while simultaneously providing safety guarantees.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge