Kuaiji: the First Chinese Accounting Large Language Model

Large Language Models (LLMs) like ChatGPT and GPT-4 have demonstrated impressive proficiency in comprehending and generating natural language. However, they encounter difficulties when tasked with adapting to specialized domains such as accounting. To address this challenge, we introduce Kuaiji, a tailored Accounting Large Language Model. Kuaiji is meticulously fine-tuned using the Baichuan framework, which encompasses continuous pre-training and supervised fine-tuning processes. Supported by CAtAcctQA, a dataset containing large genuine accountant-client dialogues, Kuaiji exhibits exceptional accuracy and response speed. Our contributions encompass the creation of the first Chinese accounting dataset, the establishment of Kuaiji as a leading open-source Chinese accounting LLM, and the validation of its efficacy through real-world accounting scenarios.

Timeseries Suppliers Allocation Risk Optimization via Deep Black Litterman Model

We introduce the BL model and the Perspective Matrix to optimize supplier selection and order allocation, focusing on both temporal and spatial dynamics. Our development of a Supplier Relationship Network, using a Spatio-Temporal Graph Neural Network, enhances the understanding of complex supplier interdependencies. Additionally, we address credibility issues in zero-order scenarios with a Masked Ranking Mechanism, improving supplier ranking efficiency. Our model demonstrates superior results on two datasets compared to the traditional models. Our evaluations using real-world datasets highlight DBLM's superiority in providing accurate predictions and precise confidence intervals, particularly in high-resolution scenarios.

Infinite-Horizon Graph Filters: Leveraging Power Series to Enhance Sparse Information Aggregation

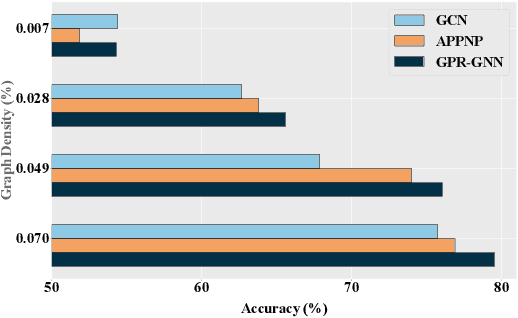
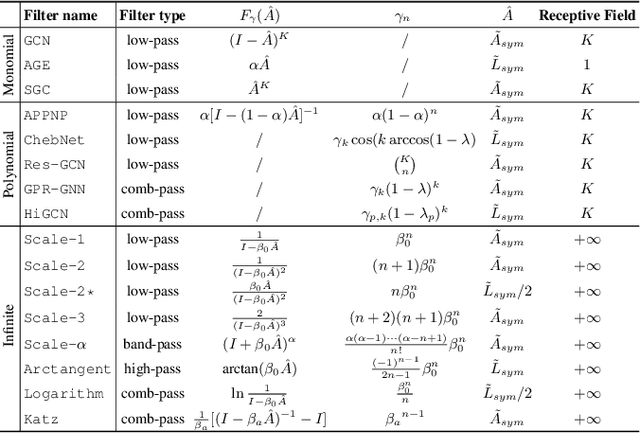
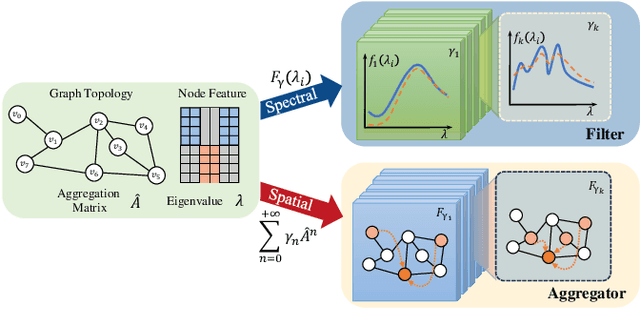
Graph Neural Networks (GNNs) have shown considerable effectiveness in a variety of graph learning tasks, particularly those based on the message-passing approach in recent years. However, their performance is often constrained by a limited receptive field, a challenge that becomes more acute in the presence of sparse graphs. In light of the power series, which possesses infinite expansion capabilities, we propose a novel Graph Power Filter Neural Network (GPFN) that enhances node classification by employing a power series graph filter to augment the receptive field. Concretely, our GPFN designs a new way to build a graph filter with an infinite receptive field based on the convergence power series, which can be analyzed in the spectral and spatial domains. Besides, we theoretically prove that our GPFN is a general framework that can integrate any power series and capture long-range dependencies. Finally, experimental results on three datasets demonstrate the superiority of our GPFN over state-of-the-art baselines.

Uncertainty Quantification via Spatial-Temporal Tweedie Model for Zero-inflated and Long-tail Travel Demand Prediction

crucial for transportation management. However, traditional spatial-temporal deep learning models grapple with addressing the sparse and long-tail characteristics in high-resolution O-D matrices and quantifying prediction uncertainty. This dilemma arises from the numerous zeros and over-dispersed demand patterns within these matrices, which challenge the Gaussian assumption inherent to deterministic deep learning models. To address these challenges, we propose a novel approach: the Spatial-Temporal Tweedie Graph Neural Network (STTD). The STTD introduces the Tweedie distribution as a compelling alternative to the traditional 'zero-inflated' model and leverages spatial and temporal embeddings to parameterize travel demand distributions. Our evaluations using real-world datasets highlight STTD's superiority in providing accurate predictions and precise confidence intervals, particularly in high-resolution scenarios.