Adaptive Elastic Training for Sparse Deep Learning on Heterogeneous Multi-GPU Servers

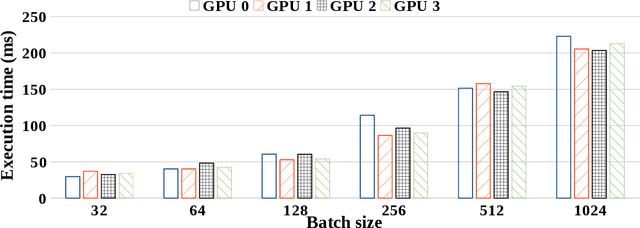
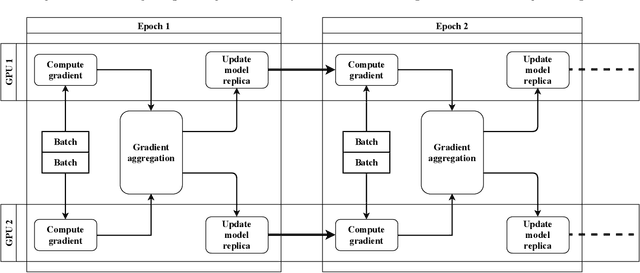
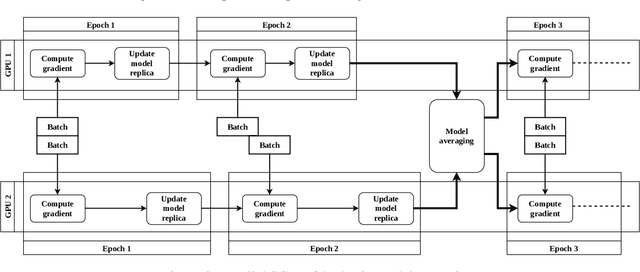
Motivated by extreme multi-label classification applications, we consider training deep learning models over sparse data in multi-GPU servers. The variance in the number of non-zero features across training batches and the intrinsic GPU heterogeneity combine to limit accuracy and increase the time to convergence. We address these challenges with Adaptive SGD, an adaptive elastic model averaging stochastic gradient descent algorithm for heterogeneous multi-GPUs that is characterized by dynamic scheduling, adaptive batch size scaling, and normalized model merging. Instead of statically partitioning batches to GPUs, batches are routed based on the relative processing speed. Batch size scaling assigns larger batches to the faster GPUs and smaller batches to the slower ones, with the goal to arrive at a steady state in which all the GPUs perform the same number of model updates. Normalized model merging computes optimal weights for every GPU based on the assigned batches such that the combined model achieves better accuracy. We show experimentally that Adaptive SGD outperforms four state-of-the-art solutions in time-to-accuracy and is scalable with the number of GPUs.

DJEnsemble: On the Selection of a Disjoint Ensemble of Deep Learning Black-Box Spatio-temporal Models

In this paper, we present a cost-based approach for the automatic selection and allocation of a disjoint ensemble of black-box predictors to answer predictive spatio-temporal queries. Our approach is divided into two parts -- offline and online. During the offline part, we preprocess the predictive domain data -- transforming it into a regular grid -- and the black-box models -- computing their spatio-temporal learning function. In the online part, we compute a DJEnsemble plan which minimizes a multivariate cost function based on estimates for the prediction error and the execution cost -- producing a model spatial allocation matrix -- and run the optimal ensemble plan. We conduct a set of extensive experiments that evaluate the DJEnsemble approach and highlight its efficiency. We show that our cost model produces plans with performance close to the actual best plan. When compared against the traditional ensemble approach, DJEnsemble achieves up to $4X$ improvement in execution time and almost $9X$ improvement in prediction accuracy. To the best of our knowledge, this is the first work to solve the problem of optimizing the allocation of black-box models to answer predictive spatio-temporal queries.

Heterogeneous CPU+GPU Stochastic Gradient Descent Algorithms

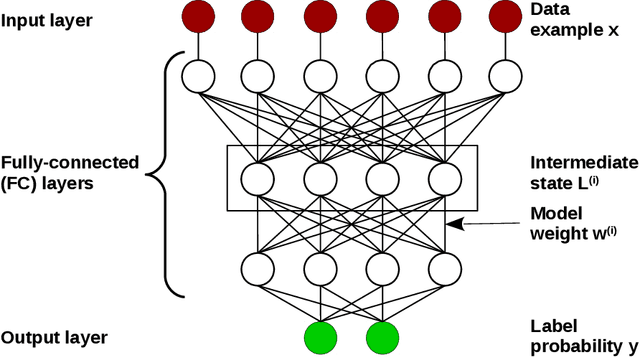
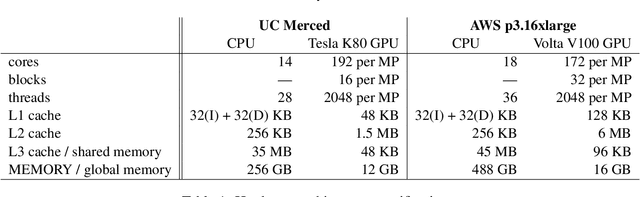
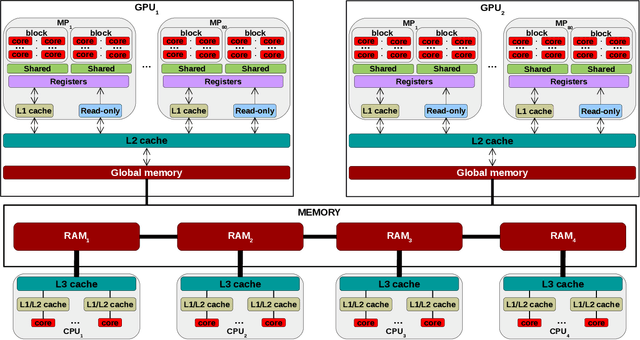
The widely-adopted practice is to train deep learning models with specialized hardware accelerators, e.g., GPUs or TPUs, due to their superior performance on linear algebra operations. However, this strategy does not employ effectively the extensive CPU and memory resources -- which are used only for preprocessing, data transfer, and scheduling -- available by default on the accelerated servers. In this paper, we study training algorithms for deep learning on heterogeneous CPU+GPU architectures. Our two-fold objective -- maximize convergence rate and resource utilization simultaneously -- makes the problem challenging. In order to allow for a principled exploration of the design space, we first introduce a generic deep learning framework that exploits the difference in computational power and memory hierarchy between CPU and GPU through asynchronous message passing. Based on insights gained through experimentation with the framework, we design two heterogeneous asynchronous stochastic gradient descent (SGD) algorithms. The first algorithm -- CPU+GPU Hogbatch -- combines small batches on CPU with large batches on GPU in order to maximize the utilization of both resources. However, this generates an unbalanced model update distribution which hinders the statistical convergence. The second algorithm -- Adaptive Hogbatch -- assigns batches with continuously evolving size based on the relative speed of CPU and GPU. This balances the model updates ratio at the expense of a customizable decrease in utilization. We show that the implementation of these algorithms in the proposed CPU+GPU framework achieves both faster convergence and higher resource utilization than TensorFlow on several real datasets and on two computing architectures -- an on-premises server and a cloud instance.

Progressive Data Science: Potential and Challenges

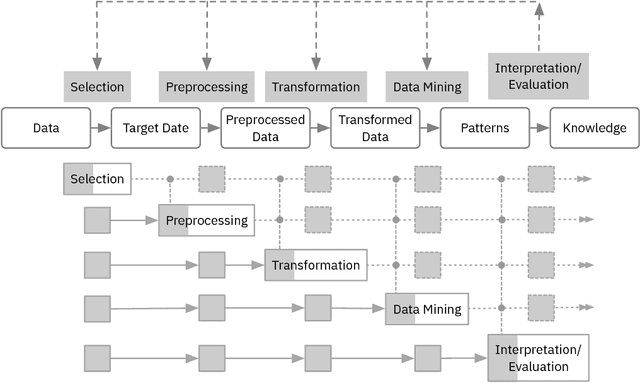
Data science requires time-consuming iterative manual activities. In particular, activities such as data selection, preprocessing, transformation, and mining, highly depend on iterative trial-and-error processes that could be sped up significantly by providing quick feedback on the impact of changes. The idea of progressive data science is to compute the results of changes in a progressive manner, returning a first approximation of results quickly and allow iterative refinements until converging to a final result. Enabling the user to interact with the intermediate results allows an early detection of erroneous or suboptimal choices, the guided definition of modifications to the pipeline and their quick assessment. In this paper, we discuss the progressiveness challenges arising in different steps of the data science pipeline. We describe how changes in each step of the pipeline impact the subsequent steps and outline why progressive data science will help to make the process more effective. Computing progressive approximations of outcomes resulting from changes creates numerous research challenges, especially if the changes are made in the early steps of the pipeline. We discuss these challenges and outline first steps towards progressiveness, which, we argue, will ultimately help to significantly speed-up the overall data science process.

Stochastic Gradient Descent on Highly-Parallel Architectures

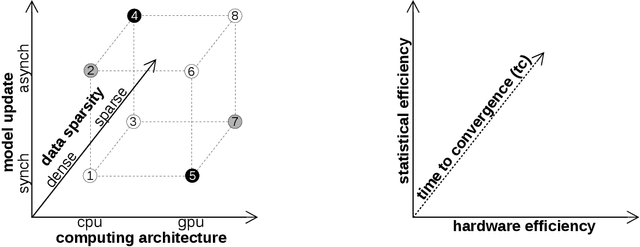
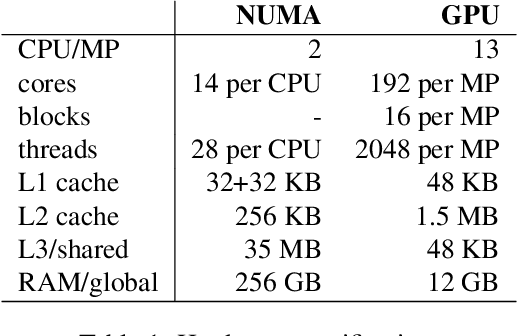
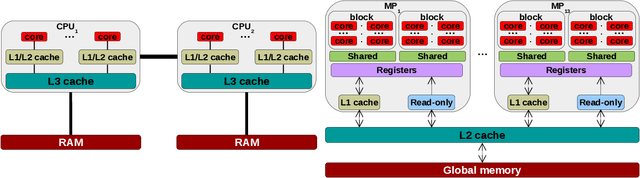
There is an increased interest in building data analytics frameworks with advanced algebraic capabilities both in industry and academia. Many of these frameworks, e.g., TensorFlow and BIDMach, implement their compute-intensive primitives in two flavors---as multi-thread routines for multi-core CPUs and as highly-parallel kernels executed on GPU. Stochastic gradient descent (SGD) is the most popular optimization method for model training implemented extensively on modern data analytics platforms. While the data-intensive properties of SGD are well-known, there is an intense debate on which of the many SGD variants is better in practice. In this paper, we perform a comprehensive study of parallel SGD for training generalized linear models. We consider the impact of three factors -- computing architecture (multi-core CPU or GPU), synchronous or asynchronous model updates, and data sparsity -- on three measures---hardware efficiency, statistical efficiency, and time to convergence. In the process, we design an optimized asynchronous SGD algorithm for GPU that leverages warp shuffling and cache coalescing for data and model access. We draw several interesting findings from our extensive experiments with logistic regression (LR) and support vector machines (SVM) on five real datasets. For synchronous SGD, GPU always outperforms parallel CPU---they both outperform a sequential CPU solution by more than 400X. For asynchronous SGD, parallel CPU is the safest choice while GPU with data replication is better in certain situations. The choice between synchronous GPU and asynchronous CPU depends on the task and the characteristics of the data. As a reference, our best implementation outperforms TensorFlow and BIDMach consistently. We hope that our insights provide a useful guide for applying parallel SGD to generalized linear models.