Stochastic Gradient Descent on Highly-Parallel Architectures
Paper and Code
Feb 24, 2018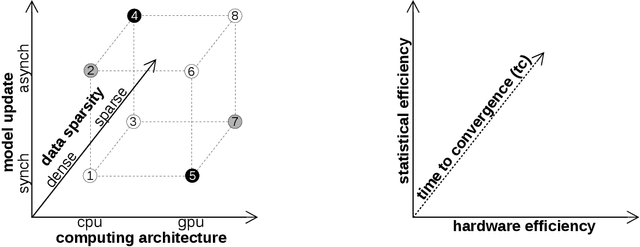
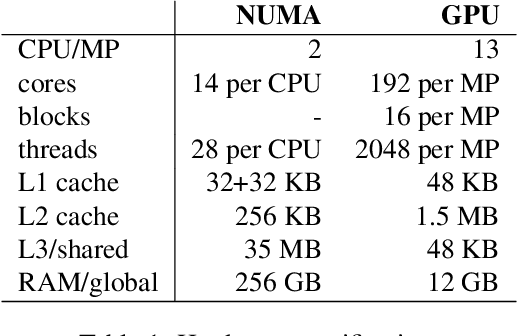

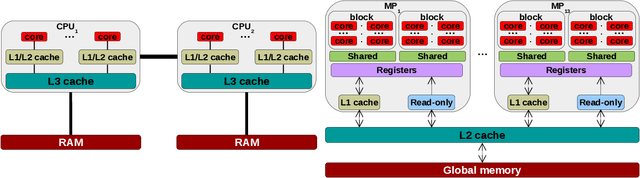
There is an increased interest in building data analytics frameworks with advanced algebraic capabilities both in industry and academia. Many of these frameworks, e.g., TensorFlow and BIDMach, implement their compute-intensive primitives in two flavors---as multi-thread routines for multi-core CPUs and as highly-parallel kernels executed on GPU. Stochastic gradient descent (SGD) is the most popular optimization method for model training implemented extensively on modern data analytics platforms. While the data-intensive properties of SGD are well-known, there is an intense debate on which of the many SGD variants is better in practice. In this paper, we perform a comprehensive study of parallel SGD for training generalized linear models. We consider the impact of three factors -- computing architecture (multi-core CPU or GPU), synchronous or asynchronous model updates, and data sparsity -- on three measures---hardware efficiency, statistical efficiency, and time to convergence. In the process, we design an optimized asynchronous SGD algorithm for GPU that leverages warp shuffling and cache coalescing for data and model access. We draw several interesting findings from our extensive experiments with logistic regression (LR) and support vector machines (SVM) on five real datasets. For synchronous SGD, GPU always outperforms parallel CPU---they both outperform a sequential CPU solution by more than 400X. For asynchronous SGD, parallel CPU is the safest choice while GPU with data replication is better in certain situations. The choice between synchronous GPU and asynchronous CPU depends on the task and the characteristics of the data. As a reference, our best implementation outperforms TensorFlow and BIDMach consistently. We hope that our insights provide a useful guide for applying parallel SGD to generalized linear models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge