SoftED: Metrics for Soft Evaluation of Time Series Event Detection

Time series event detection methods are evaluated mainly by standard classification metrics that focus solely on detection accuracy. However, inaccuracy in detecting an event can often result from its preceding or delayed effects reflected in neighboring detections. These detections are valuable to trigger necessary actions or help mitigate unwelcome consequences. In this context, current metrics are insufficient and inadequate for the context of event detection. There is a demand for metrics that incorporate both the concept of time and temporal tolerance for neighboring detections. This paper introduces SoftED metrics, a new set of metrics designed for soft evaluating event detection methods. They enable the evaluation of both detection accuracy and the degree to which their detections represent events. They improved event detection evaluation by associating events and their representative detections, incorporating temporal tolerance in over 36\% of experiments compared to the usual classification metrics. SoftED metrics were validated by domain specialists that indicated their contribution to detection evaluation and method selection.

Algorithmic Probability of Large Datasets and the Simplicity Bubble Problem in Machine Learning

When mining large datasets in order to predict new data, limitations of the principles behind statistical machine learning pose a serious challenge not only to the Big Data deluge, but also to the traditional assumptions that data generating processes are biased toward low algorithmic complexity. Even when one assumes an underlying algorithmic-informational bias toward simplicity in finite dataset generators, we show that fully automated, with or without access to pseudo-random generators, computable learning algorithms, in particular those of statistical nature used in current approaches to machine learning (including deep learning), can always be deceived, naturally or artificially, by sufficiently large datasets. In particular, we demonstrate that, for every finite learning algorithm, there is a sufficiently large dataset size above which the algorithmic probability of an unpredictable deceiver is an upper bound (up to a multiplicative constant that only depends on the learning algorithm) for the algorithmic probability of any other larger dataset. In other words, very large and complex datasets are as likely to deceive learning algorithms into a "simplicity bubble" as any other particular dataset. These deceiving datasets guarantee that any prediction will diverge from the high-algorithmic-complexity globally optimal solution while converging toward the low-algorithmic-complexity locally optimal solution. We discuss the framework and empirical conditions for circumventing this deceptive phenomenon, moving away from statistical machine learning towards a stronger type of machine learning based on, or motivated by, the intrinsic power of algorithmic information theory and computability theory.

Hyperspherical embedding for novel class classification

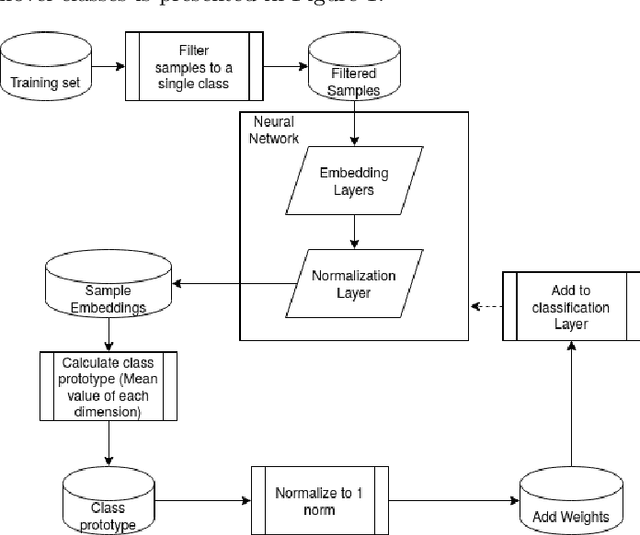
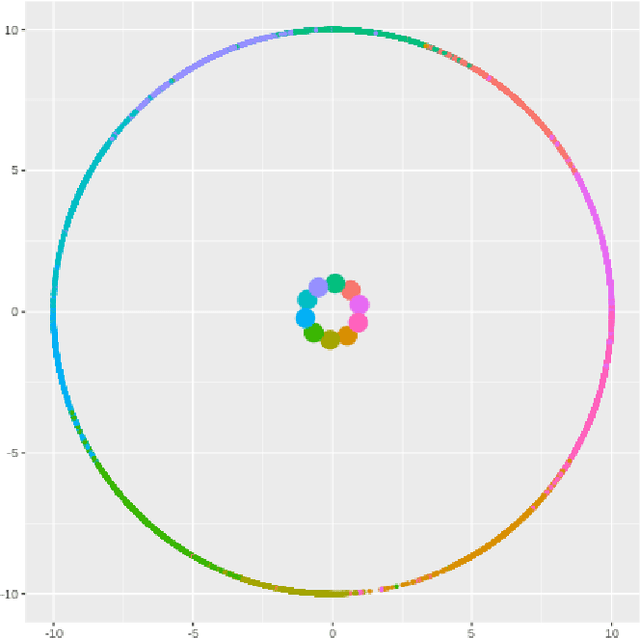
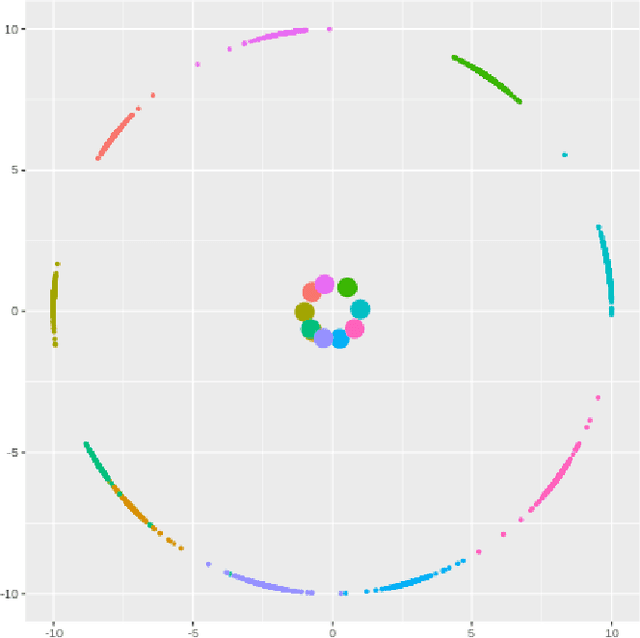
Deep learning models have become increasingly useful in many different industries. On the domain of image classification, convolutional neural networks proved the ability to learn robust features for the closed set problem, as shown in many different datasets, such as MNIST FASHIONMNIST, CIFAR10, CIFAR100, and IMAGENET. These approaches use deep neural networks with dense layers with softmax activation functions in order to learn features that can separate classes in a latent space. However, this traditional approach is not useful for identifying classes unseen on the training set, known as the open set problem. A similar problem occurs in scenarios involving learning on small data. To tackle both problems, few-shot learning has been proposed. In particular, metric learning learns features that obey constraints of a metric distance in the latent space in order to perform classification. However, while this approach proves to be useful for the open set problem, current implementation requires pair-wise training, where both positive and negative examples of similar images are presented during the training phase, which limits the applicability of these approaches in large data or large class scenarios given the combinatorial nature of the possible inputs.In this paper, we present a constraint-based approach applied to the representations in the latent space under the normalized softmax loss, proposed by[18]. We experimentally validate the proposed approach for the classification of unseen classes on different datasets using both metric learning and the normalized softmax loss, on disjoint and joint scenarios. Our results show that not only our proposed strategy can be efficiently trained on larger set of classes, as it does not require pairwise learning, but also present better classification results than the metric learning strategies surpassing its accuracy by a significant margin.

DJEnsemble: On the Selection of a Disjoint Ensemble of Deep Learning Black-Box Spatio-temporal Models

In this paper, we present a cost-based approach for the automatic selection and allocation of a disjoint ensemble of black-box predictors to answer predictive spatio-temporal queries. Our approach is divided into two parts -- offline and online. During the offline part, we preprocess the predictive domain data -- transforming it into a regular grid -- and the black-box models -- computing their spatio-temporal learning function. In the online part, we compute a DJEnsemble plan which minimizes a multivariate cost function based on estimates for the prediction error and the execution cost -- producing a model spatial allocation matrix -- and run the optimal ensemble plan. We conduct a set of extensive experiments that evaluate the DJEnsemble approach and highlight its efficiency. We show that our cost model produces plans with performance close to the actual best plan. When compared against the traditional ensemble approach, DJEnsemble achieves up to $4X$ improvement in execution time and almost $9X$ improvement in prediction accuracy. To the best of our knowledge, this is the first work to solve the problem of optimizing the allocation of black-box models to answer predictive spatio-temporal queries.

STConvS2S: Spatiotemporal Convolutional Sequence to Sequence Network for Weather Forecasting

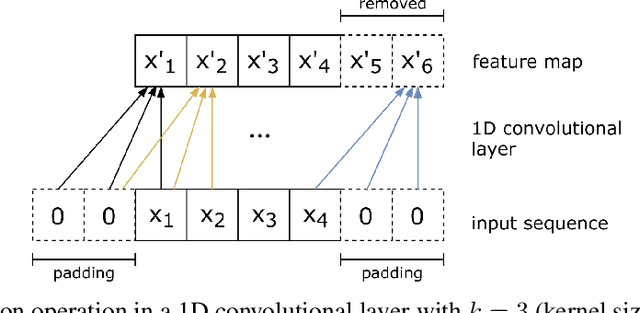
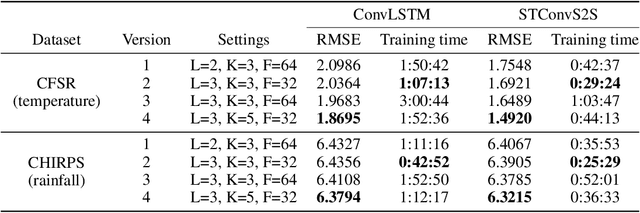
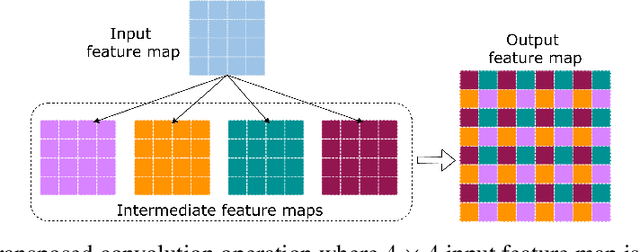
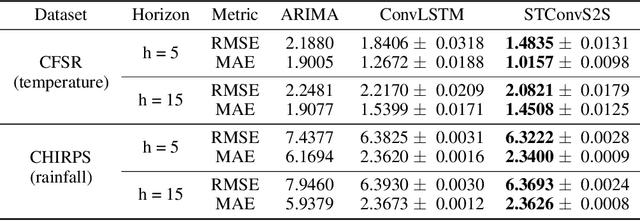
Applying machine learning models to meteorological data brings many opportunities to the Geosciences field, such as predicting future weather conditions more accurately. In recent years, modeling meteorological data with deep neural networks has become a relevant area of investigation. These works apply either recurrent neural networks (RNNs) or some hybrid approach mixing RNNs and convolutional neural networks (CNNs). In this work, we propose STConvS2S (short for Spatiotemporal Convolutional Sequence to Sequence Network), a new deep learning architecture built for learning both spatial and temporal data dependencies in weather data, using fully convolutional layers. Computational experiments using observations of air temperature and rainfall show that our architecture captures spatiotemporal context and outperforms baseline models and the state-of-art architecture for weather forecasting task.

Parallel Computation of PDFs on Big Spatial Data Using Spark

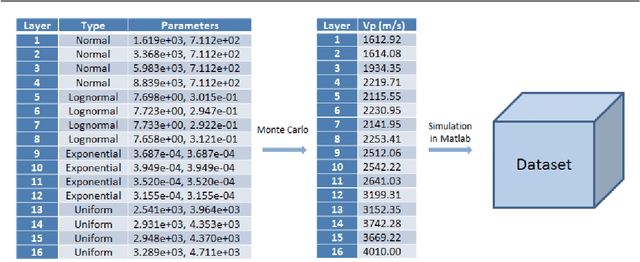
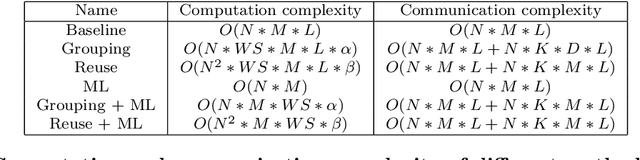
We consider big spatial data, which is typically produced in scientific areas such as geological or seismic interpretation. The spatial data can be produced by observation (e.g. using sensors or soil instrument) or numerical simulation programs and correspond to points that represent a 3D soil cube area. However, errors in signal processing and modeling create some uncertainty, and thus a lack of accuracy in identifying geological or seismic phenomenons. Such uncertainty must be carefully analyzed. To analyze uncertainty, the main solution is to compute a Probability Density Function (PDF) of each point in the spatial cube area. However, computing PDFs on big spatial data can be very time consuming (from several hours to even months on a parallel computer). In this paper, we propose a new solution to efficiently compute such PDFs in parallel using Spark, with three methods: data grouping, machine learning prediction and sampling. We evaluate our solution by extensive experiments on different computer clusters using big data ranging from hundreds of GB to several TB. The experimental results show that our solution scales up very well and can reduce the execution time by a factor of 33 (in the order of seconds or minutes) compared with a baseline method.

A note on the complexity of the causal ordering problem

In this note we provide a concise report on the complexity of the causal ordering problem, originally introduced by Simon to reason about causal dependencies implicit in systems of mathematical equations. We show that Simon's classical algorithm to infer causal ordering is NP-Hard---an intractability previously guessed but never proven. We present then a detailed account based on Nayak's suggested algorithmic solution (the best available), which is dominated by computing transitive closure---bounded in time by $O(|\mathcal V|\cdot |\mathcal S|)$, where $\mathcal S(\mathcal E, \mathcal V)$ is the input system structure composed of a set $\mathcal E$ of equations over a set $\mathcal V$ of variables with number of variable appearances (density) $|\mathcal S|$. We also comment on the potential of causal ordering for emerging applications in large-scale hypothesis management and analytics.