The State of Sparse Training in Deep Reinforcement Learning

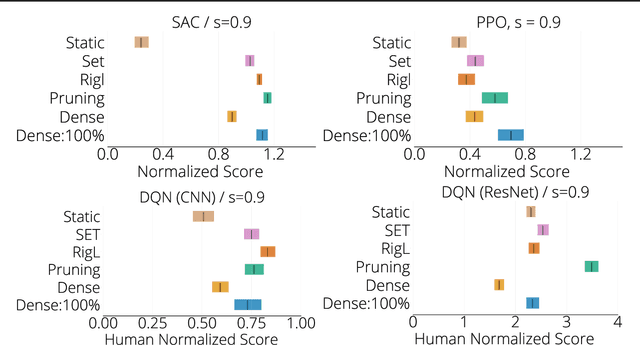
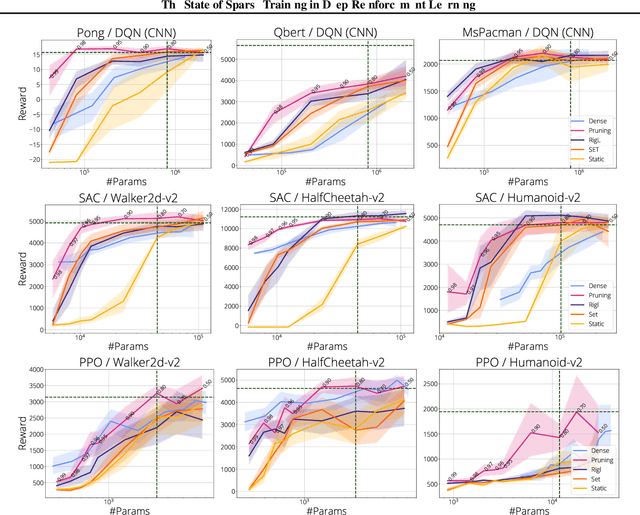
The use of sparse neural networks has seen rapid growth in recent years, particularly in computer vision. Their appeal stems largely from the reduced number of parameters required to train and store, as well as in an increase in learning efficiency. Somewhat surprisingly, there have been very few efforts exploring their use in Deep Reinforcement Learning (DRL). In this work we perform a systematic investigation into applying a number of existing sparse training techniques on a variety of DRL agents and environments. Our results corroborate the findings from sparse training in the computer vision domain - sparse networks perform better than dense networks for the same parameter count - in the DRL domain. We provide detailed analyses on how the various components in DRL are affected by the use of sparse networks and conclude by suggesting promising avenues for improving the effectiveness of sparse training methods, as well as for advancing their use in DRL.

Training Compute-Optimal Large Language Models

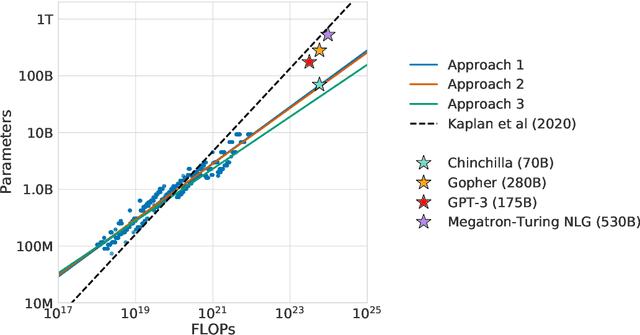
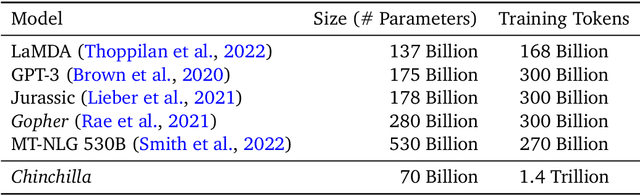
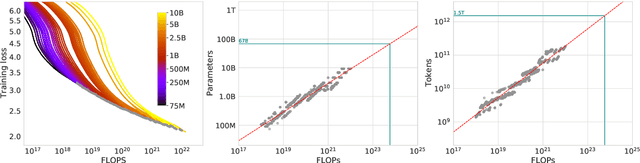
We investigate the optimal model size and number of tokens for training a transformer language model under a given compute budget. We find that current large language models are significantly undertrained, a consequence of the recent focus on scaling language models whilst keeping the amount of training data constant. By training over \nummodels language models ranging from 70 million to over 16 billion parameters on 5 to 500 billion tokens, we find that for compute-optimal training, the model size and the number of training tokens should be scaled equally: for every doubling of model size the number of training tokens should also be doubled. We test this hypothesis by training a predicted compute-optimal model, \chinchilla, that uses the same compute budget as \gopher but with 70B parameters and 4$\times$ more more data. \chinchilla uniformly and significantly outperforms \Gopher (280B), GPT-3 (175B), Jurassic-1 (178B), and Megatron-Turing NLG (530B) on a large range of downstream evaluation tasks. This also means that \chinchilla uses substantially less compute for fine-tuning and inference, greatly facilitating downstream usage. As a highlight, \chinchilla reaches a state-of-the-art average accuracy of 67.5\% on the MMLU benchmark, greater than a 7\% improvement over \gopher.

Unified Scaling Laws for Routed Language Models

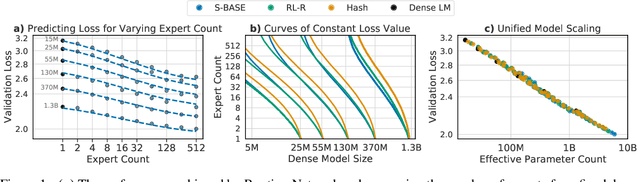
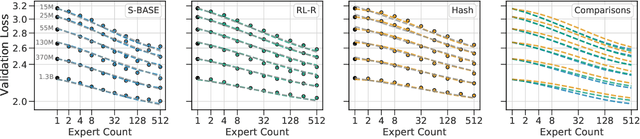
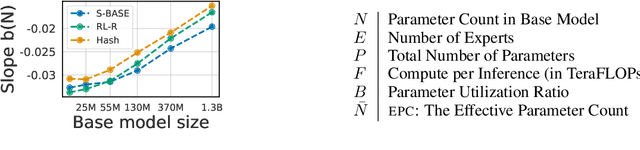
The performance of a language model has been shown to be effectively modeled as a power-law in its parameter count. Here we study the scaling behaviors of Routing Networks: architectures that conditionally use only a subset of their parameters while processing an input. For these models, parameter count and computational requirement form two independent axes along which an increase leads to better performance. In this work we derive and justify scaling laws defined on these two variables which generalize those known for standard language models and describe the performance of a wide range of routing architectures trained via three different techniques. Afterwards we provide two applications of these laws: first deriving an Effective Parameter Count along which all models scale at the same rate, and then using the scaling coefficients to give a quantitative comparison of the three routing techniques considered. Our analysis derives from an extensive evaluation of Routing Networks across five orders of magnitude of size, including models with hundreds of experts and hundreds of billions of parameters.

Improving language models by retrieving from trillions of tokens

We enhance auto-regressive language models by conditioning on document chunks retrieved from a large corpus, based on local similarity with preceding tokens. With a $2$ trillion token database, our Retrieval-Enhanced Transformer (RETRO) obtains comparable performance to GPT-3 and Jurassic-1 on the Pile, despite using 25$\times$ fewer parameters. After fine-tuning, RETRO performance translates to downstream knowledge-intensive tasks such as question answering. RETRO combines a frozen Bert retriever, a differentiable encoder and a chunked cross-attention mechanism to predict tokens based on an order of magnitude more data than what is typically consumed during training. We typically train RETRO from scratch, yet can also rapidly RETROfit pre-trained transformers with retrieval and still achieve good performance. Our work opens up new avenues for improving language models through explicit memory at unprecedented scale.

Step-unrolled Denoising Autoencoders for Text Generation

In this paper we propose a new generative model of text, Step-unrolled Denoising Autoencoder (SUNDAE), that does not rely on autoregressive models. Similarly to denoising diffusion techniques, SUNDAE is repeatedly applied on a sequence of tokens, starting from random inputs and improving them each time until convergence. We present a simple new improvement operator that converges in fewer iterations than diffusion methods, while qualitatively producing better samples on natural language datasets. SUNDAE achieves state-of-the-art results (among non-autoregressive methods) on the WMT'14 English-to-German translation task and good qualitative results on unconditional language modeling on the Colossal Cleaned Common Crawl dataset and a dataset of Python code from GitHub. The non-autoregressive nature of SUNDAE opens up possibilities beyond left-to-right prompted generation, by filling in arbitrary blank patterns in a template.

Scaling Language Models: Methods, Analysis & Insights from Training Gopher

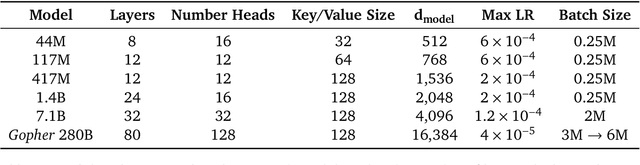
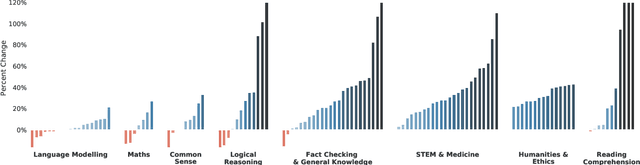
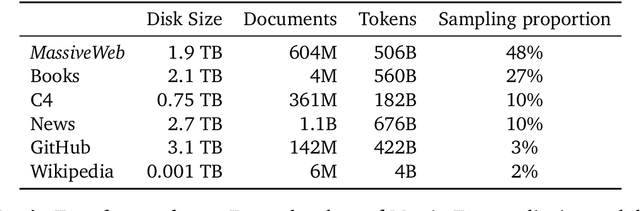
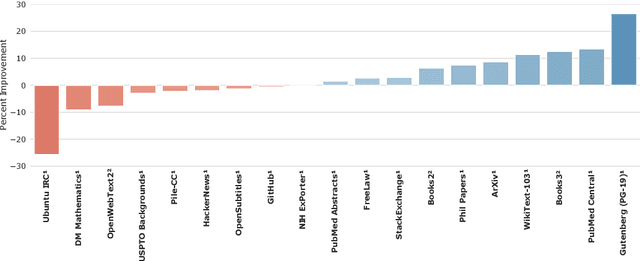
Language modelling provides a step towards intelligent communication systems by harnessing large repositories of written human knowledge to better predict and understand the world. In this paper, we present an analysis of Transformer-based language model performance across a wide range of model scales -- from models with tens of millions of parameters up to a 280 billion parameter model called Gopher. These models are evaluated on 152 diverse tasks, achieving state-of-the-art performance across the majority. Gains from scale are largest in areas such as reading comprehension, fact-checking, and the identification of toxic language, but logical and mathematical reasoning see less benefit. We provide a holistic analysis of the training dataset and model's behaviour, covering the intersection of model scale with bias and toxicity. Finally we discuss the application of language models to AI safety and the mitigation of downstream harms.

Top-KAST: Top-K Always Sparse Training

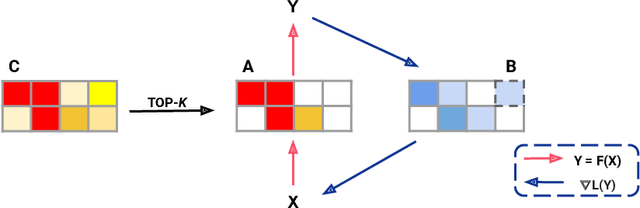
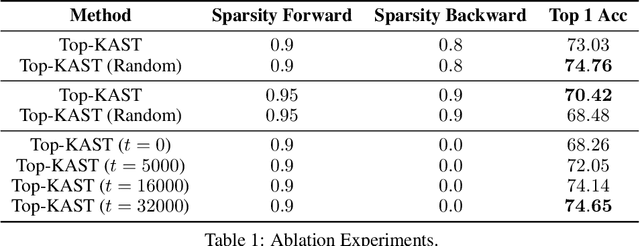
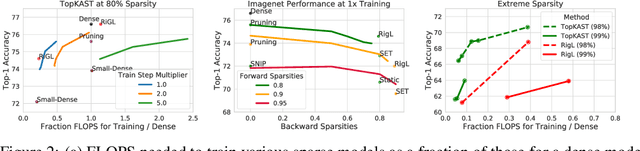
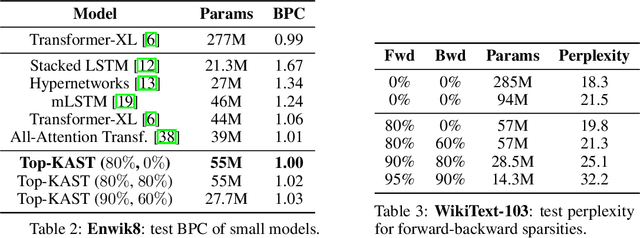
Sparse neural networks are becoming increasingly important as the field seeks to improve the performance of existing models by scaling them up, while simultaneously trying to reduce power consumption and computational footprint. Unfortunately, most existing methods for inducing performant sparse models still entail the instantiation of dense parameters, or dense gradients in the backward-pass, during training. For very large models this requirement can be prohibitive. In this work we propose Top-KAST, a method that preserves constant sparsity throughout training (in both the forward and backward-passes). We demonstrate the efficacy of our approach by showing that it performs comparably to or better than previous works when training models on the established ImageNet benchmark, whilst fully maintaining sparsity. In addition to our ImageNet results, we also demonstrate our approach in the domain of language modeling where the current best performing architectures tend to have tens of billions of parameters and scaling up does not yet seem to have saturated performance. Sparse versions of these architectures can be run with significantly fewer resources, making them more widely accessible and applicable. Furthermore, in addition to being effective, our approach is straightforward and can easily be implemented in a wide range of existing machine learning frameworks with only a few additional lines of code. We therefore hope that our contribution will help enable the broader community to explore the potential held by massive models, without incurring massive computational cost.

On the Generalization Benefit of Noise in Stochastic Gradient Descent

It has long been argued that minibatch stochastic gradient descent can generalize better than large batch gradient descent in deep neural networks. However recent papers have questioned this claim, arguing that this effect is simply a consequence of suboptimal hyperparameter tuning or insufficient compute budgets when the batch size is large. In this paper, we perform carefully designed experiments and rigorous hyperparameter sweeps on a range of popular models, which verify that small or moderately large batch sizes can substantially outperform very large batches on the test set. This occurs even when both models are trained for the same number of iterations and large batches achieve smaller training losses. Our results confirm that the noise in stochastic gradients can enhance generalization. We study how the optimal learning rate schedule changes as the epoch budget grows, and we provide a theoretical account of our observations based on the stochastic differential equation perspective of SGD dynamics.

Sparse GPU Kernels for Deep Learning

Scientific workloads have traditionally exploited high levels of sparsity to accelerate computation and reduce memory requirements. While deep neural networks can be made sparse, achieving practical speedups on GPUs is difficult because these applications have relatively moderate levels of sparsity that are not sufficient for existing sparse kernels to outperform their dense counterparts. In this work, we study sparse matrices from deep learning applications and identify favorable properties that can be exploited to accelerate computation. Based on these insights, we develop high-performance GPU kernels for two sparse matrix operations widely applicable in neural networks: sparse matrix-dense matrix multiplication and sampled dense-dense matrix multiplication. Our kernels reach 27% of single-precision peak on Nvidia V100 GPUs. Using our kernels, we demonstrate sparse Transformer and MobileNet models that achieve 1.2-2.1x speedups and up to 12.8x memory savings without sacrificing accuracy.

AlgebraNets

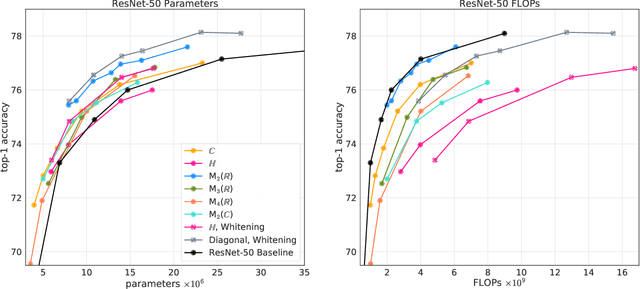
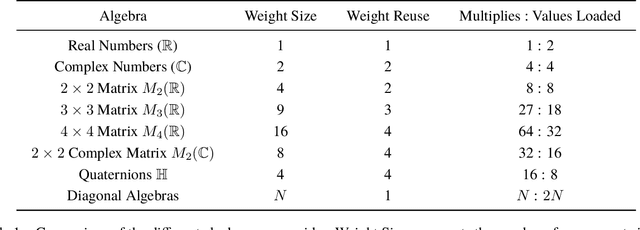
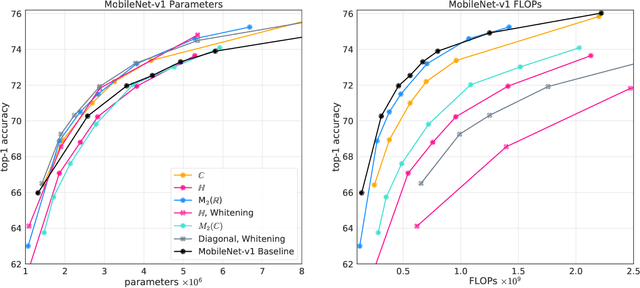
Neural networks have historically been built layerwise from the set of functions in ${f: \mathbb{R}^n \to \mathbb{R}^m }$, i.e. with activations and weights/parameters represented by real numbers, $\mathbb{R}$. Our work considers a richer set of objects for activations and weights, and undertakes a comprehensive study of alternative algebras as number representations by studying their performance on two challenging problems: large-scale image classification using the ImageNet dataset and language modeling using the enwiki8 and WikiText-103 datasets. We denote this broader class of models as AlgebraNets. Our findings indicate that the conclusions of prior work, which explored neural networks constructed from $\mathbb{C}$ (complex numbers) and $\mathbb{H}$ (quaternions) on smaller datasets, do not always transfer to these challenging settings. However, our results demonstrate that there are alternative algebras which deliver better parameter and computational efficiency compared with $\mathbb{R}$. We consider $\mathbb{C}$, $\mathbb{H}$, $M_{2}(\mathbb{R})$ (the set of $2\times2$ real-valued matrices), $M_{2}(\mathbb{C})$, $M_{3}(\mathbb{R})$ and $M_{4}(\mathbb{R})$. Additionally, we note that multiplication in these algebras has higher compute density than real multiplication, a useful property in situations with inherently limited parameter reuse such as auto-regressive inference and sparse neural networks. We therefore investigate how to induce sparsity within AlgebraNets. We hope that our strong results on large-scale, practical benchmarks will spur further exploration of these unconventional architectures which challenge the default choice of using real numbers for neural network weights and activations.