Sparse GPU Kernels for Deep Learning
Paper and Code
Jun 18, 2020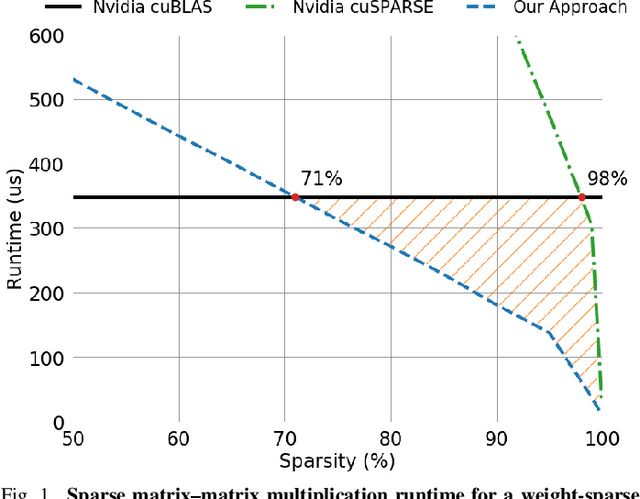
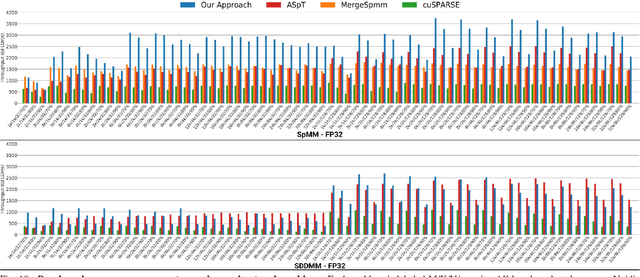
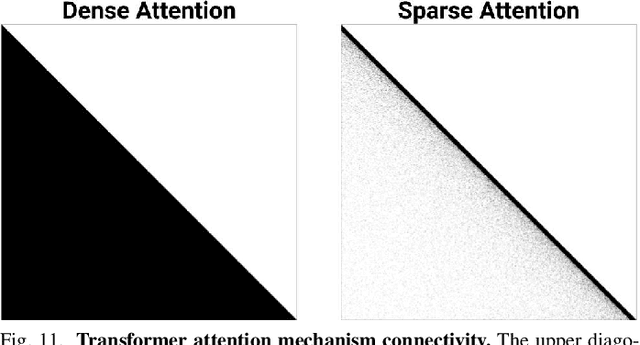
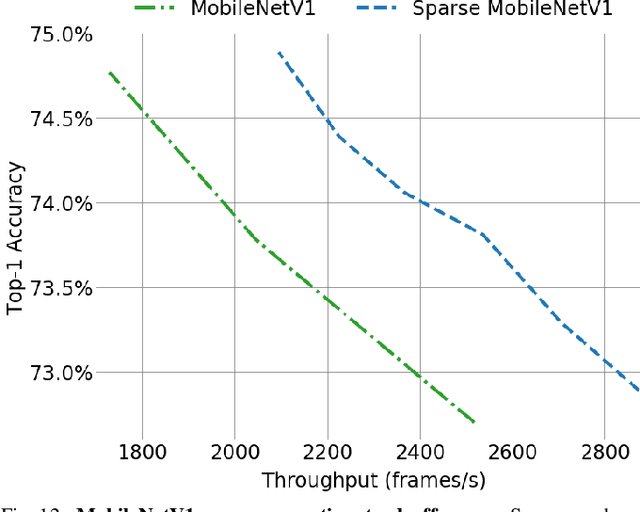
Scientific workloads have traditionally exploited high levels of sparsity to accelerate computation and reduce memory requirements. While deep neural networks can be made sparse, achieving practical speedups on GPUs is difficult because these applications have relatively moderate levels of sparsity that are not sufficient for existing sparse kernels to outperform their dense counterparts. In this work, we study sparse matrices from deep learning applications and identify favorable properties that can be exploited to accelerate computation. Based on these insights, we develop high-performance GPU kernels for two sparse matrix operations widely applicable in neural networks: sparse matrix-dense matrix multiplication and sampled dense-dense matrix multiplication. Our kernels reach 27% of single-precision peak on Nvidia V100 GPUs. Using our kernels, we demonstrate sparse Transformer and MobileNet models that achieve 1.2-2.1x speedups and up to 12.8x memory savings without sacrificing accuracy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge