AlgebraNets
Paper and Code
Jun 16, 2020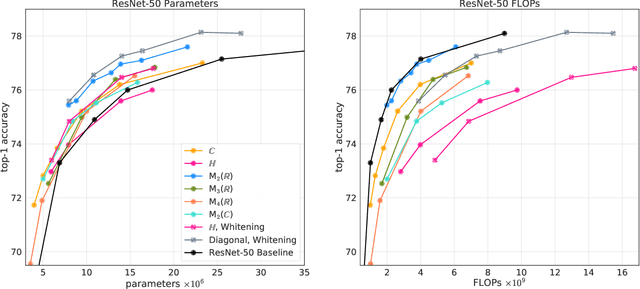
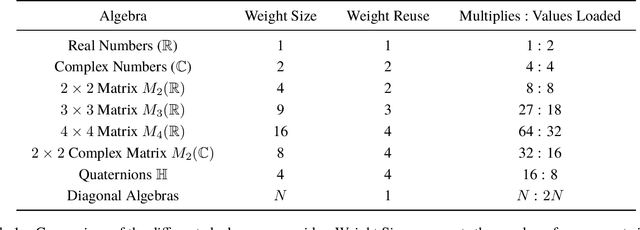
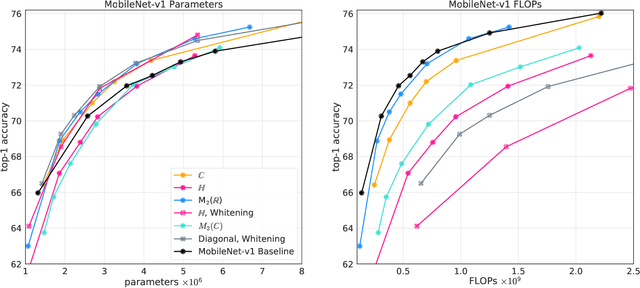

Neural networks have historically been built layerwise from the set of functions in ${f: \mathbb{R}^n \to \mathbb{R}^m }$, i.e. with activations and weights/parameters represented by real numbers, $\mathbb{R}$. Our work considers a richer set of objects for activations and weights, and undertakes a comprehensive study of alternative algebras as number representations by studying their performance on two challenging problems: large-scale image classification using the ImageNet dataset and language modeling using the enwiki8 and WikiText-103 datasets. We denote this broader class of models as AlgebraNets. Our findings indicate that the conclusions of prior work, which explored neural networks constructed from $\mathbb{C}$ (complex numbers) and $\mathbb{H}$ (quaternions) on smaller datasets, do not always transfer to these challenging settings. However, our results demonstrate that there are alternative algebras which deliver better parameter and computational efficiency compared with $\mathbb{R}$. We consider $\mathbb{C}$, $\mathbb{H}$, $M_{2}(\mathbb{R})$ (the set of $2\times2$ real-valued matrices), $M_{2}(\mathbb{C})$, $M_{3}(\mathbb{R})$ and $M_{4}(\mathbb{R})$. Additionally, we note that multiplication in these algebras has higher compute density than real multiplication, a useful property in situations with inherently limited parameter reuse such as auto-regressive inference and sparse neural networks. We therefore investigate how to induce sparsity within AlgebraNets. We hope that our strong results on large-scale, practical benchmarks will spur further exploration of these unconventional architectures which challenge the default choice of using real numbers for neural network weights and activations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge