Dmitrii Marin
Token Pooling in Vision Transformers
Oct 11, 2021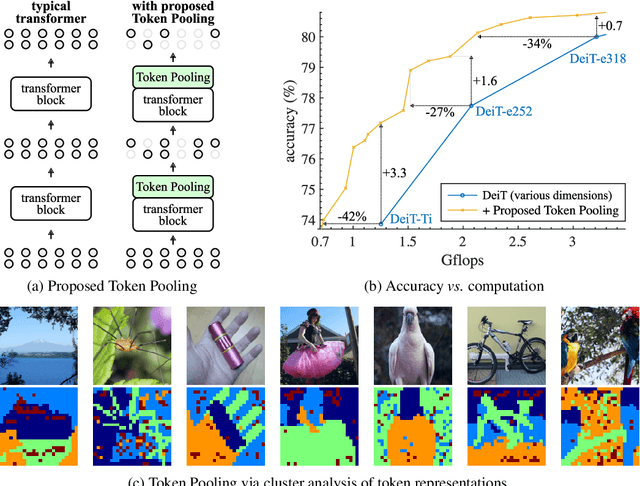
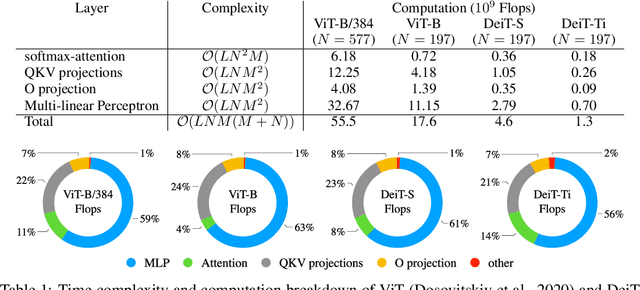
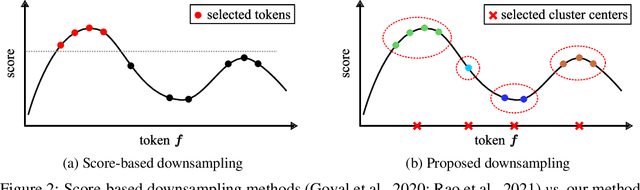
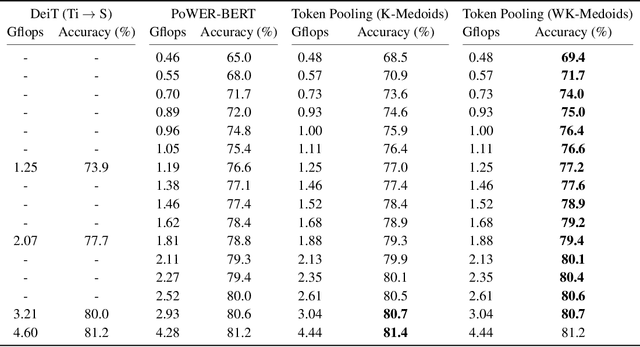
Abstract:Despite the recent success in many applications, the high computational requirements of vision transformers limit their use in resource-constrained settings. While many existing methods improve the quadratic complexity of attention, in most vision transformers, self-attention is not the major computation bottleneck, e.g., more than 80% of the computation is spent on fully-connected layers. To improve the computational complexity of all layers, we propose a novel token downsampling method, called Token Pooling, efficiently exploiting redundancies in the images and intermediate token representations. We show that, under mild assumptions, softmax-attention acts as a high-dimensional low-pass (smoothing) filter. Thus, its output contains redundancy that can be pruned to achieve a better trade-off between the computational cost and accuracy. Our new technique accurately approximates a set of tokens by minimizing the reconstruction error caused by downsampling. We solve this optimization problem via cost-efficient clustering. We rigorously analyze and compare to prior downsampling methods. Our experiments show that Token Pooling significantly improves the cost-accuracy trade-off over the state-of-the-art downsampling. Token Pooling is a simple and effective operator that can benefit many architectures. Applied to DeiT, it achieves the same ImageNet top-1 accuracy using 42% fewer computations.
Robust Trust Region for Weakly Supervised Segmentation
Apr 05, 2021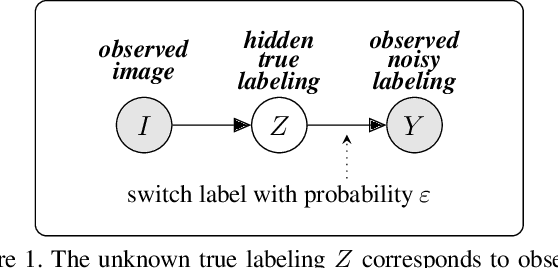

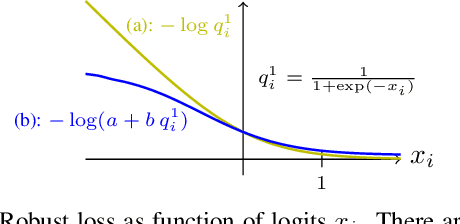
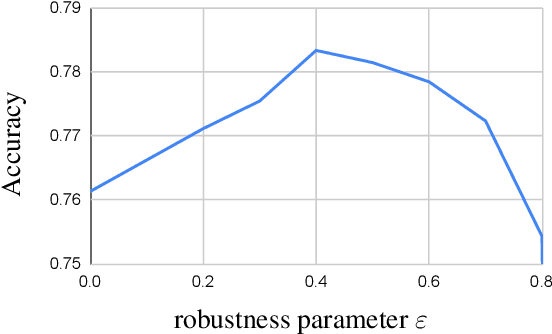
Abstract:Acquisition of training data for the standard semantic segmentation is expensive if requiring that each pixel is labeled. Yet, current methods significantly deteriorate in weakly supervised settings, e.g. where a fraction of pixels is labeled or when only image-level tags are available. It has been shown that regularized losses - originally developed for unsupervised low-level segmentation and representing geometric priors on pixel labels - can considerably improve the quality of weakly supervised training. However, many common priors require optimization stronger than gradient descent. Thus, such regularizers have limited applicability in deep learning. We propose a new robust trust region approach for regularized losses improving the state-of-the-art results. Our approach can be seen as a higher-order generalization of the classic chain rule. It allows neural network optimization to use strong low-level solvers for the corresponding regularizers, including discrete ones.
Confluent Vessel Trees with Accurate Bifurcations
Mar 26, 2021
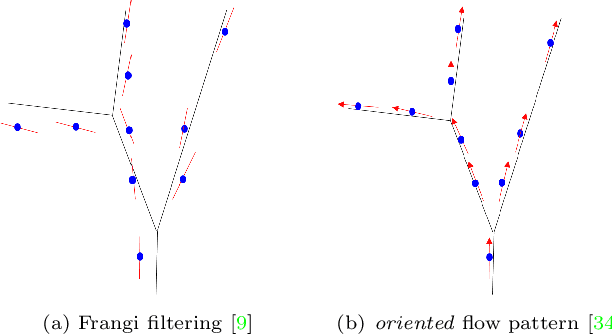
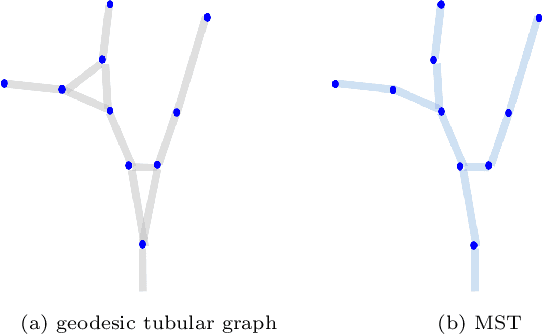

Abstract:We are interested in unsupervised reconstruction of complex near-capillary vasculature with thousands of bifurcations where supervision and learning are infeasible. Unsupervised methods can use many structural constraints, e.g. topology, geometry, physics. Common techniques use variants of MST on geodesic tubular graphs minimizing symmetric pairwise costs, i.e. distances. We show limitations of such standard undirected tubular graphs producing typical errors at bifurcations where flow "directedness" is critical. We introduce a new general concept of confluence for continuous oriented curves forming vessel trees and show how to enforce it on discrete tubular graphs. While confluence is a high-order property, we present an efficient practical algorithm for reconstructing confluent vessel trees using minimum arborescence on a directed graph enforcing confluence via simple flow-extrapolating arc construction. Empirical tests on large near-capillary sub-voxel vasculature volumes demonstrate significantly improved reconstruction accuracy at bifurcations. Our code has also been made publicly available.
Efficient Segmentation: Learning Downsampling Near Semantic Boundaries
Jul 16, 2019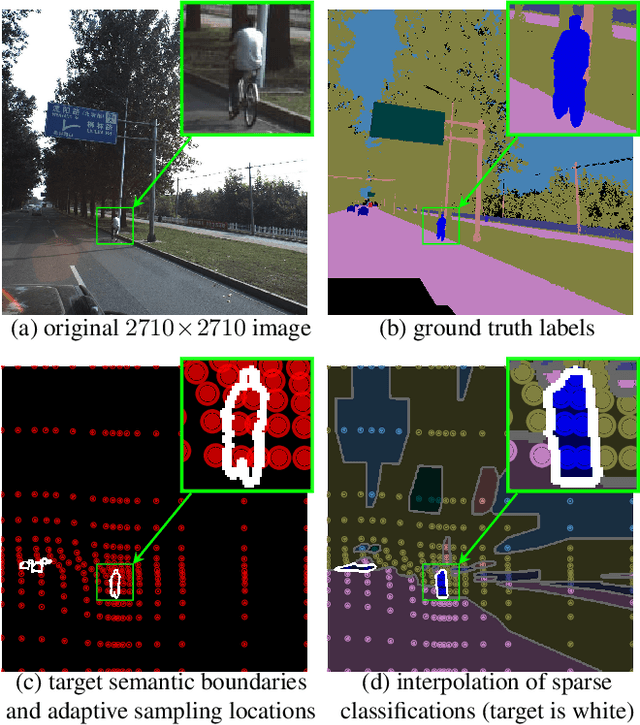
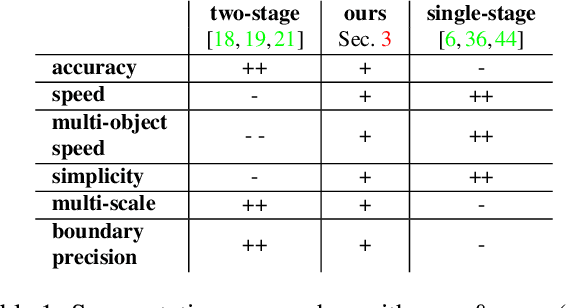
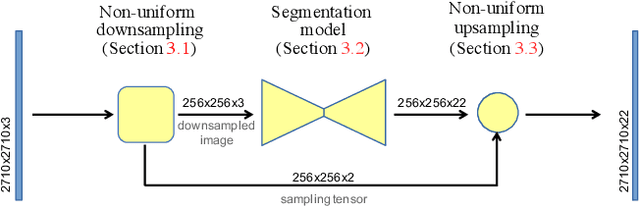
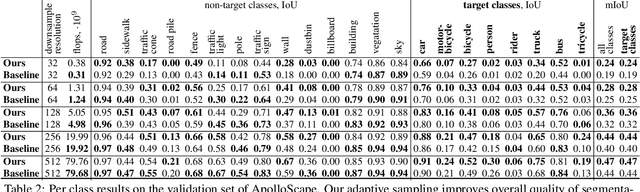
Abstract:Many automated processes such as auto-piloting rely on a good semantic segmentation as a critical component. To speed up performance, it is common to downsample the input frame. However, this comes at the cost of missed small objects and reduced accuracy at semantic boundaries. To address this problem, we propose a new content-adaptive downsampling technique that learns to favor sampling locations near semantic boundaries of target classes. Cost-performance analysis shows that our method consistently outperforms the uniform sampling improving balance between accuracy and computational efficiency. Our adaptive sampling gives segmentation with better quality of boundaries and more reliable support for smaller-size objects.
Divergence Prior and Vessel-tree Reconstruction
Nov 24, 2018



Abstract:We propose a new geometric regularization principle for reconstructing vector fields based on prior knowledge about their divergence. As one important example of this general idea, we focus on vector fields modelling blood flow pattern that should be divergent in arteries and convergent in veins. We show that this previously ignored regularization constraint can significantly improve the quality of vessel tree reconstruction particularly around bifurcations where non-zero divergence is concentrated. Our divergence prior is critical for resolving (binary) sign ambiguity in flow orientations produced by standard vessel filters, e.g. Frangi. Our vessel tree centerline reconstruction combines divergence constraints with robust curvature regularization. Our unsupervised method can reconstruct complete vessel trees with near-capillary details on synthetic and real 3D volumes.
ADM for grid CRF loss in CNN segmentation
Sep 07, 2018



Abstract:Variants of gradient descent (GD) dominate CNN loss minimization in computer vision. But, as we show, some powerful loss functions are practically useless only due to their poor optimization by GD. In the context of weakly-supervised CNN segmentation, we present a general ADM approach to regularized losses, which are inspired by well-known MRF/CRF models in "shallow" segmentation. While GD fails on the popular nearest-neighbor Potts loss, ADM splitting with $\alpha$-expansion solver significantly improves optimization of such grid CRF losses yielding state-of-the-art training quality. Denser CRF losses become amenable to basic GD, but they produce lower quality object boundaries in agreement with known noisy performance of dense CRF inference in shallow segmentation.
Kernel clustering: density biases and solutions
Dec 06, 2017



Abstract:Kernel methods are popular in clustering due to their generality and discriminating power. However, we show that many kernel clustering criteria have density biases theoretically explaining some practically significant artifacts empirically observed in the past. For example, we provide conditions and formally prove the density mode isolation bias in kernel K-means for a common class of kernels. We call it Breiman's bias due to its similarity to the histogram mode isolation previously discovered by Breiman in decision tree learning with Gini impurity. We also extend our analysis to other popular kernel clustering methods, e.g. average/normalized cut or dominant sets, where density biases can take different forms. For example, splitting isolated points by cut-based criteria is essentially the sparsest subset bias, which is the opposite of the density mode bias. Our findings suggest that a principled solution for density biases in kernel clustering should directly address data inhomogeneity. We show that density equalization can be implicitly achieved using either locally adaptive weights or locally adaptive kernels. Moreover, density equalization makes many popular kernel clustering objectives equivalent. Our synthetic and real data experiments illustrate density biases and proposed solutions. We anticipate that theoretical understanding of kernel clustering limitations and their principled solutions will be important for a broad spectrum of data analysis applications across the disciplines.
Kernel Cuts: MRF meets Kernel & Spectral Clustering
Sep 21, 2016



Abstract:We propose a new segmentation model combining common regularization energies, e.g. Markov Random Field (MRF) potentials, and standard pairwise clustering criteria like Normalized Cut (NC), average association (AA), etc. These clustering and regularization models are widely used in machine learning and computer vision, but they were not combined before due to significant differences in the corresponding optimization, e.g. spectral relaxation and combinatorial max-flow techniques. On the one hand, we show that many common applications using MRF segmentation energies can benefit from a high-order NC term, e.g. enforcing balanced clustering of arbitrary high-dimensional image features combining color, texture, location, depth, motion, etc. On the other hand, standard clustering applications can benefit from an inclusion of common pairwise or higher-order MRF constraints, e.g. edge alignment, bin-consistency, label cost, etc. To address joint energies like NC+MRF, we propose efficient Kernel Cut algorithms based on bound optimization. While focusing on graph cut and move-making techniques, our new unary (linear) kernel and spectral bound formulations for common pairwise clustering criteria allow to integrate them with any regularization functionals with existing discrete or continuous solvers.
Thin Structure Estimation with Curvature Regularization
Sep 16, 2015



Abstract:Many applications in vision require estimation of thin structures such as boundary edges, surfaces, roads, blood vessels, neurons, etc. Unlike most previous approaches, we simultaneously detect and delineate thin structures with sub-pixel localization and real-valued orientation estimation. This is an ill-posed problem that requires regularization. We propose an objective function combining detection likelihoods with a prior minimizing curvature of the center-lines or surfaces. Unlike simple block-coordinate descent, we develop a novel algorithm that is able to perform joint optimization of location and detection variables more effectively. Our lower bound optimization algorithm applies to quadratic or absolute curvature. The proposed early vision framework is sufficiently general and it can be used in many higher-level applications. We illustrate the advantage of our approach on a range of 2D and 3D examples.
* D. Marin, Y. Zhong, M. Drangova, Y. Boykov. Thin Structure Estimation with Curvature Regularization. International Conference on Computer Vision (ICCV), Santiago, Chili, December 2015, to appear
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge