Collision Cross-entropy and EM Algorithm for Self-labeled Classification

We propose "collision cross-entropy" as a robust alternative to the Shannon's cross-entropy in the context of self-labeled classification with posterior models. Assuming unlabeled data, self-labeling works by estimating latent pseudo-labels, categorical distributions y, that optimize some discriminative clustering criteria, e.g. "decisiveness" and "fairness". All existing self-labeled losses incorporate Shannon's cross-entropy term targeting the model prediction, softmax, at the estimated distribution y. In fact, softmax is trained to mimic the uncertainty in y exactly. Instead, we propose the negative log-likelihood of "collision" to maximize the probability of equality between two random variables represented by distributions softmax and y. We show that our loss satisfies some properties of a generalized cross-entropy. Interestingly, it agrees with the Shannon's cross-entropy for one-hot pseudo-labels y, but the training from softer labels weakens. For example, if y is a uniform distribution at some data point, it has zero contribution to the training. Our self-labeling loss combining collision cross entropy with basic clustering criteria is convex w.r.t. pseudo-labels, but non-trivial to optimize over the probability simplex. We derive a practical EM algorithm optimizing pseudo-labels y significantly faster than generic methods, e.g. the projectile gradient descent. The collision cross-entropy consistently improves the results on multiple self-labeled clustering examples using different DNNs.

Revisiting Discriminative Entropy Clustering and its relation to K-means

Maximization of mutual information between the model's input and output is formally related to "decisiveness" and "fairness" of the softmax predictions, motivating such unsupervised entropy-based losses for discriminative neural networks. Recent self-labeling methods based on such losses represent the state of the art in deep clustering. However, some important properties of entropy clustering are not well-known, or even misunderstood. For example, we provide a counterexample to prior claims about equivalence to variance clustering (K-means) and point out technical mistakes in such theories. We discuss the fundamental differences between these discriminative and generative clustering approaches. Moreover, we show the susceptibility of standard entropy clustering to narrow margins and motivate an explicit margin maximization term. We also propose an improved self-labeling loss; it is robust to pseudo-labeling errors and enforces stronger fairness. We develop an EM algorithm for our loss that is significantly faster than the standard alternatives. Our results improve the state-of-the-art on standard benchmarks.

Confluent Vessel Trees with Accurate Bifurcations

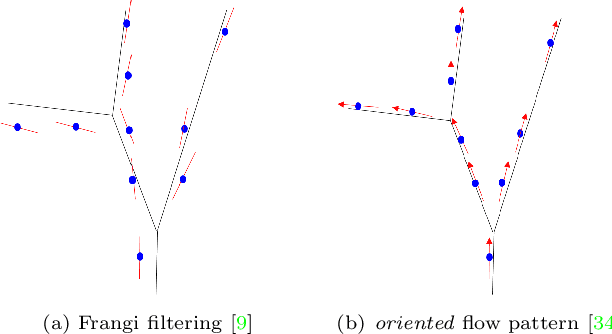
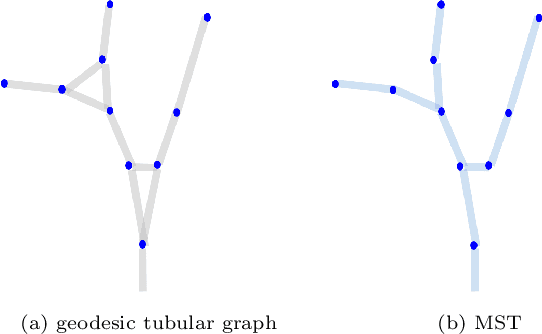
We are interested in unsupervised reconstruction of complex near-capillary vasculature with thousands of bifurcations where supervision and learning are infeasible. Unsupervised methods can use many structural constraints, e.g. topology, geometry, physics. Common techniques use variants of MST on geodesic tubular graphs minimizing symmetric pairwise costs, i.e. distances. We show limitations of such standard undirected tubular graphs producing typical errors at bifurcations where flow "directedness" is critical. We introduce a new general concept of confluence for continuous oriented curves forming vessel trees and show how to enforce it on discrete tubular graphs. While confluence is a high-order property, we present an efficient practical algorithm for reconstructing confluent vessel trees using minimum arborescence on a directed graph enforcing confluence via simple flow-extrapolating arc construction. Empirical tests on large near-capillary sub-voxel vasculature volumes demonstrate significantly improved reconstruction accuracy at bifurcations. Our code has also been made publicly available.

Divergence Prior and Vessel-tree Reconstruction

We propose a new geometric regularization principle for reconstructing vector fields based on prior knowledge about their divergence. As one important example of this general idea, we focus on vector fields modelling blood flow pattern that should be divergent in arteries and convergent in veins. We show that this previously ignored regularization constraint can significantly improve the quality of vessel tree reconstruction particularly around bifurcations where non-zero divergence is concentrated. Our divergence prior is critical for resolving (binary) sign ambiguity in flow orientations produced by standard vessel filters, e.g. Frangi. Our vessel tree centerline reconstruction combines divergence constraints with robust curvature regularization. Our unsupervised method can reconstruct complete vessel trees with near-capillary details on synthetic and real 3D volumes.