Confluent Vessel Trees with Accurate Bifurcations
Paper and Code
Mar 26, 2021
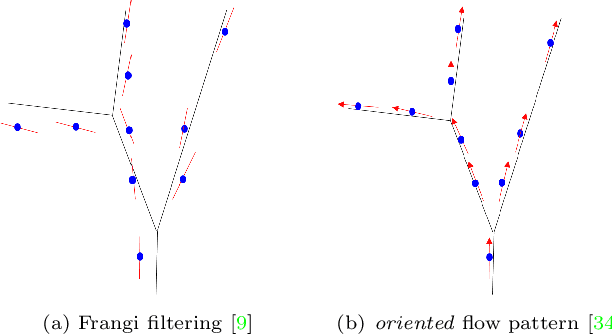
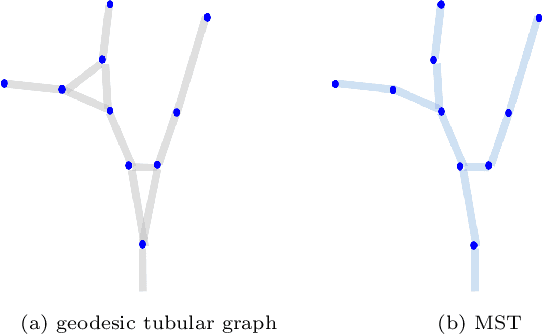

We are interested in unsupervised reconstruction of complex near-capillary vasculature with thousands of bifurcations where supervision and learning are infeasible. Unsupervised methods can use many structural constraints, e.g. topology, geometry, physics. Common techniques use variants of MST on geodesic tubular graphs minimizing symmetric pairwise costs, i.e. distances. We show limitations of such standard undirected tubular graphs producing typical errors at bifurcations where flow "directedness" is critical. We introduce a new general concept of confluence for continuous oriented curves forming vessel trees and show how to enforce it on discrete tubular graphs. While confluence is a high-order property, we present an efficient practical algorithm for reconstructing confluent vessel trees using minimum arborescence on a directed graph enforcing confluence via simple flow-extrapolating arc construction. Empirical tests on large near-capillary sub-voxel vasculature volumes demonstrate significantly improved reconstruction accuracy at bifurcations. Our code has also been made publicly available.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge