Diffusion Models for Video Prediction and Infilling

To predict and anticipate future outcomes or reason about missing information in a sequence is a key ability for agents to be able to make intelligent decisions. This requires strong temporally coherent generative capabilities. Diffusion models have shown huge success in several generative tasks lately, but have not been extensively explored in the video domain. We present Random-Mask Video Diffusion (RaMViD), which extends image diffusion models to videos using 3D convolutions, and introduces a new conditioning technique during training. By varying the mask we condition on, the model is able to perform video prediction, infilling and upsampling. Since we do not use concatenation to condition on a mask, as done in most conditionally trained diffusion models, we are able to decrease the memory footprint. We evaluated the model on two benchmark datasets for video prediction and one for video generation on which we achieved competitive results. On Kinetics-600 we achieved state-of-the-art for video prediction.

Few-Shot Diffusion Models

Denoising diffusion probabilistic models (DDPM) are powerful hierarchical latent variable models with remarkable sample generation quality and training stability. These properties can be attributed to parameter sharing in the generative hierarchy, as well as a parameter-free diffusion-based inference procedure. In this paper, we present Few-Shot Diffusion Models (FSDM), a framework for few-shot generation leveraging conditional DDPMs. FSDMs are trained to adapt the generative process conditioned on a small set of images from a given class by aggregating image patch information using a set-based Vision Transformer (ViT). At test time, the model is able to generate samples from previously unseen classes conditioned on as few as 5 samples from that class. We empirically show that FSDM can perform few-shot generation and transfer to new datasets. We benchmark variants of our method on complex vision datasets for few-shot learning and compare to unconditional and conditional DDPM baselines. Additionally, we show how conditioning the model on patch-based input set information improves training convergence.

Sampling in Combinatorial Spaces with SurVAE Flow Augmented MCMC

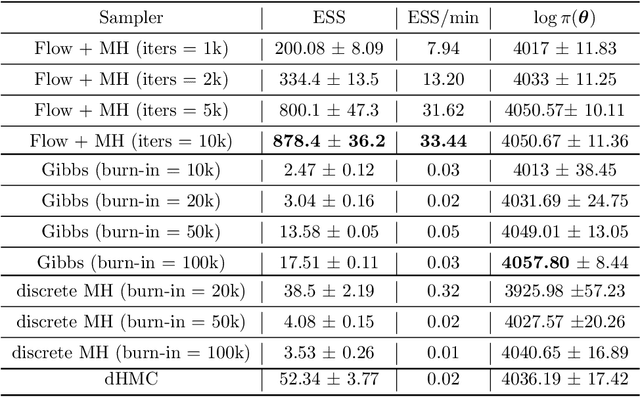
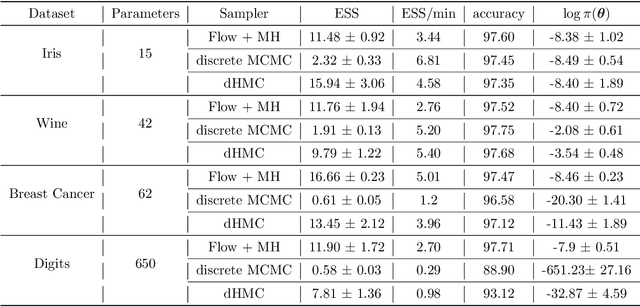
Hybrid Monte Carlo is a powerful Markov Chain Monte Carlo method for sampling from complex continuous distributions. However, a major limitation of HMC is its inability to be applied to discrete domains due to the lack of gradient signal. In this work, we introduce a new approach based on augmenting Monte Carlo methods with SurVAE Flows to sample from discrete distributions using a combination of neural transport methods like normalizing flows and variational dequantization, and the Metropolis-Hastings rule. Our method first learns a continuous embedding of the discrete space using a surjective map and subsequently learns a bijective transformation from the continuous space to an approximately Gaussian distributed latent variable. Sampling proceeds by simulating MCMC chains in the latent space and mapping these samples to the target discrete space via the learned transformations. We demonstrate the efficacy of our algorithm on a range of examples from statistics, computational physics and machine learning, and observe improvements compared to alternative algorithms.

Argmax Flows and Multinomial Diffusion: Towards Non-Autoregressive Language Models

The field of language modelling has been largely dominated by autoregressive models, for which sampling is inherently difficult to parallelize. This paper introduces two new classes of generative models for categorical data such as language or image segmentation: Argmax Flows and Multinomial Diffusion. Argmax Flows are defined by a composition of a continuous distribution (such as a normalizing flow), and an argmax function. To optimize this model, we learn a probabilistic inverse for the argmax that lifts the categorical data to a continuous space. Multinomial Diffusion gradually adds categorical noise in a diffusion process, for which the generative denoising process is learned. We demonstrate that our models perform competitively on language modelling and modelling of image segmentation maps.

SurVAE Flows: Surjections to Bridge the Gap between VAEs and Flows

Normalizing flows and variational autoencoders are powerful generative models that can represent complicated density functions. However, they both impose constraints on the models: Normalizing flows use bijective transformations to model densities whereas VAEs learn stochastic transformations that are non-invertible and thus typically do not provide tractable estimates of the marginal likelihood. In this paper, we introduce SurVAE Flows: A modular framework of composable transformations that encompasses VAEs and normalizing flows. SurVAE Flows bridge the gap between normalizing flows and VAEs with surjective transformations, wherein the transformations are deterministic in one direction -- thereby allowing exact likelihood computation, and stochastic in the reverse direction -- hence providing a lower bound on the corresponding likelihood. We show that several recently proposed methods, including dequantization and augmented normalizing flows, can be expressed as SurVAE Flows. Finally, we introduce common operations such as the max value, the absolute value, sorting and stochastic permutation as composable layers in SurVAE Flows.

Closing the Dequantization Gap: PixelCNN as a Single-Layer Flow

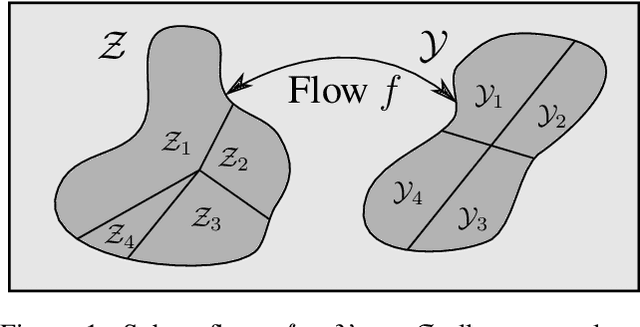
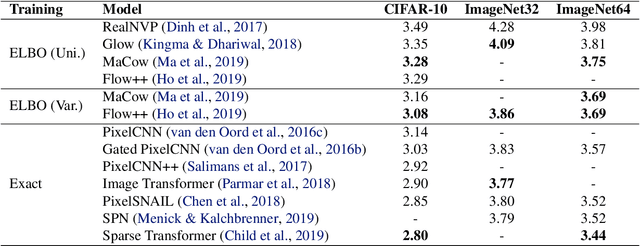
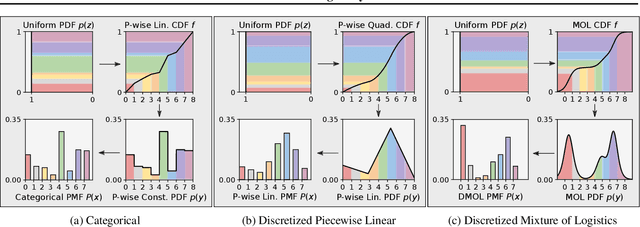
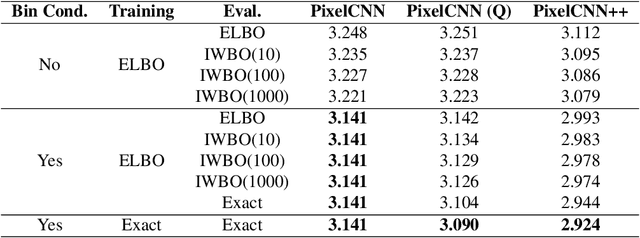
Flow models have recently made great progress at modeling quantized sensor data such as images and audio. Due to the continuous nature of flow models, dequantization is typically applied when using them for such quantized data. In this paper, we propose subset flows, a class of flows which can tractably transform subsets of the input space in one pass. As a result, they can be applied directly to quantized data without the need for dequantization. Based on this class of flows, we present a novel interpretation of several existing autoregressive models, including WaveNet and PixelCNN, as single-layer flow models defined through an invertible transformation between uniform noise and data samples. This interpretation suggests that these existing models, 1) admit a latent representation of data and 2) can be stacked in multiple flow layers. We demonstrate this by exploring the latent space of a PixelCNN and by stacking PixelCNNs in multiple flow layers.

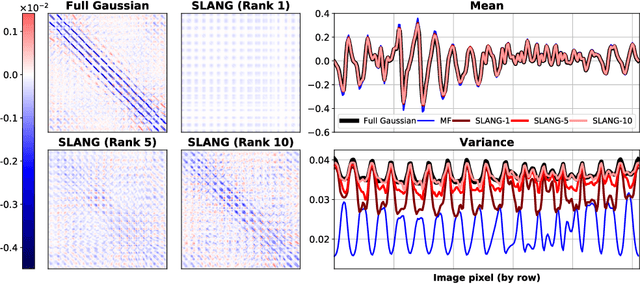
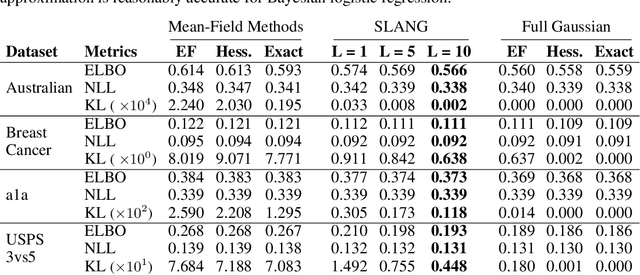
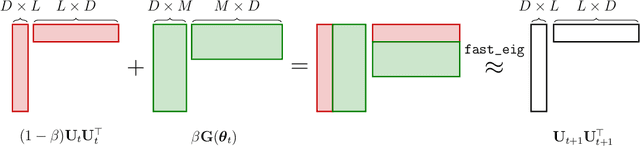
SLANG: Fast Structured Covariance Approximations for Bayesian Deep Learning with Natural Gradient

Uncertainty estimation in large deep-learning models is a computationally challenging task, where it is difficult to form even a Gaussian approximation to the posterior distribution. In such situations, existing methods usually resort to a diagonal approximation of the covariance matrix despite, the fact that these matrices are known to give poor uncertainty estimates. To address this issue, we propose a new stochastic, low-rank, approximate natural-gradient (SLANG) method for variational inference in large, deep models. Our method estimates a "diagonal plus low-rank" structure based solely on back-propagated gradients of the network log-likelihood. This requires strictly less gradient computations than methods that compute the gradient of the whole variational objective. Empirical evaluations on standard benchmarks confirm that SLANG enables faster and more accurate estimation of uncertainty than mean-field methods, and performs comparably to state-of-the-art methods.

Fast and Scalable Bayesian Deep Learning by Weight-Perturbation in Adam

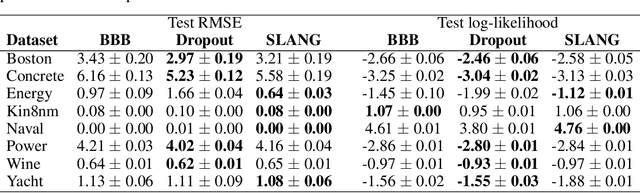
Uncertainty computation in deep learning is essential to design robust and reliable systems. Variational inference (VI) is a promising approach for such computation, but requires more effort to implement and execute compared to maximum-likelihood methods. In this paper, we propose new natural-gradient algorithms to reduce such efforts for Gaussian mean-field VI. Our algorithms can be implemented within the Adam optimizer by perturbing the network weights during gradient evaluations, and uncertainty estimates can be cheaply obtained by using the vector that adapts the learning rate. This requires lower memory, computation, and implementation effort than existing VI methods, while obtaining uncertainty estimates of comparable quality. Our empirical results confirm this and further suggest that the weight-perturbation in our algorithm could be useful for exploration in reinforcement learning and stochastic optimization.

Fast yet Simple Natural-Gradient Descent for Variational Inference in Complex Models

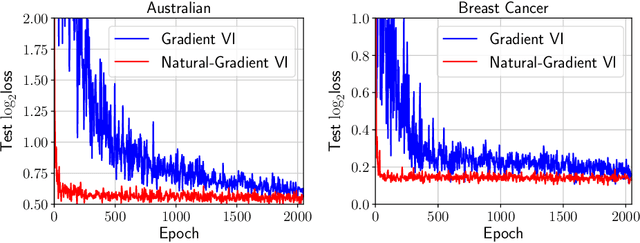
Bayesian inference plays an important role in advancing machine learning, but faces computational challenges when applied to complex models such as deep neural networks. Variational inference circumvents these challenges by formulating Bayesian inference as an optimization problem and solving it using gradient-based optimization. In this paper, we argue in favor of natural-gradient approaches which, unlike their gradient-based counterparts, can improve convergence by exploiting the information geometry of the solutions. We show how to derive fast yet simple natural-gradient updates by using a duality associated with exponential-family distributions. An attractive feature of these methods is that, by using natural-gradients, they are able to extract accurate local approximations for individual model components. We summarize recent results for Bayesian deep learning showing the superiority of natural-gradient approaches over their gradient counterparts.

Variational Adaptive-Newton Method for Explorative Learning

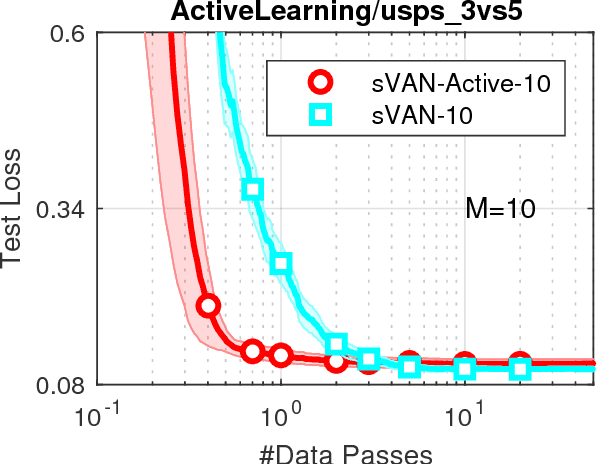
We present the Variational Adaptive Newton (VAN) method which is a black-box optimization method especially suitable for explorative-learning tasks such as active learning and reinforcement learning. Similar to Bayesian methods, VAN estimates a distribution that can be used for exploration, but requires computations that are similar to continuous optimization methods. Our theoretical contribution reveals that VAN is a second-order method that unifies existing methods in distinct fields of continuous optimization, variational inference, and evolution strategies. Our experimental results show that VAN performs well on a wide-variety of learning tasks. This work presents a general-purpose explorative-learning method that has the potential to improve learning in areas such as active learning and reinforcement learning.