Multi-Channel Factor Analysis: Identifiability and Asymptotics

Recent work by Ram\'irez et al. [2] has introduced Multi-Channel Factor Analysis (MFA) as an extension of factor analysis to multi-channel data that allows for latent factors common to all channels as well as factors specific to each channel. This paper validates the MFA covariance model and analyzes the statistical properties of the MFA estimators. In particular, a thorough investigation of model identifiability under varying latent factor structures is conducted, and sufficient conditions for generic global identifiability of MFA are obtained. The development of these identifiability conditions enables asymptotic analysis of estimators obtained by maximizing a Gaussian likelihood, which are shown to be consistent and asymptotically normal even under misspecification of the latent factor distribution.

One-Bit Target Detection in Collocated MIMO Radar with Colored Background Noise

One-bit sampling has emerged as a promising technique in multiple-input multiple-output (MIMO) radar systems due to its ability to significantly reduce data volume and processing requirements. Nevertheless, current detection methods have not adequately addressed the impact of colored noise, which is frequently encountered in real scenarios. In this paper, we present a novel detection method that accounts for colored noise in MIMO radar systems. Specifically, we derive Rao's test by computing the derivative of the likelihood function with respect to the target reflectivity parameter and the Fisher information matrix, resulting in a detector that takes the form of a weighted matched filter. To ensure the constant false alarm rate (CFAR) property, we also consider noise covariance uncertainty and examine its effect on the probability of false alarm. The detection probability is also studied analytically. Simulation results demonstrate that the proposed detector provides considerable performance gains in the presence of colored noise.

Passive detection of a random signal common to multi-sensor reference and surveillance arrays

This paper addresses the passive detection of a common rank-one subspace signal received in two multi-sensor arrays. We consider the case of a one-antenna transmitter sending a common Gaussian signal, independent Gaussian noises with arbitrary spatial covariance, and known channel subspaces. The detector derived in this paper is a generalized likelihood ratio (GLR) test. For all but one of the unknown parameters, it is possible to find closed-form maximum likelihood (ML) estimator functions. We can further compress the likelihood to only an unknown vector whose ML estimate requires maximizing a product of ratios in quadratic forms, which is carried out using a trust-region algorithm. We propose two approximations of the GLR that do not require any numerical optimization: one based on a sample-based estimator of the unknown parameter whose ML estimate cannot be obtained in closed-form, and one derived under low-SNR conditions. Notably, all the detectors are scale-invariant, and the approximations are functions of beamformed data. However, they are not GLRTs for data that has been pre-processed with a beamformer, a point that is elaborated in the paper. These detectors outperform previously published correlation detectors on simulated data, in many cases quite significantly. Moreover, performance results quantify the performance gains over detectors that assume only the dimension of the subspace to be known.

Interpretable Spectral Variational AutoEncoder (ISVAE) for time series clustering

The best encoding is the one that is interpretable in nature. In this work, we introduce a novel model that incorporates an interpretable bottleneck-termed the Filter Bank (FB)-at the outset of a Variational Autoencoder (VAE). This arrangement compels the VAE to attend on the most informative segments of the input signal, fostering the learning of a novel encoding ${f_0}$ which boasts enhanced interpretability and clusterability over traditional latent spaces. By deliberately constraining the VAE with this FB, we intentionally constrict its capacity to access broad input domain information, promoting the development of an encoding that is discernible, separable, and of reduced dimensionality. The evolutionary learning trajectory of ${f_0}$ further manifests as a dynamic hierarchical tree, offering profound insights into cluster similarities. Additionally, for handling intricate data configurations, we propose a tailored decoder structure that is symmetrically aligned with FB's architecture. Empirical evaluations highlight the superior efficacy of ISVAE, which compares favorably to state-of-the-art results in clustering metrics across real-world datasets.

One-Bit Spectrum Sensing for Cognitive Radio

Spectrum sensing in cognitive radio necessitates effective monitoring of wide bandwidths, which requires high-rate sampling. Traditional spectrum sensing methods employing high-precision analog-to-digital converters (ADCs) result in increased power consumption and expensive hardware costs. In this paper, we explore blind spectrum sensing utilizing one-bit ADCs. We derive a closed-form detector based on Rao's test and demonstrate its equivalence with the second-order eigenvalue-moment-ratio test. Furthermore, a near-exact distribution based on the moment-based method, and an approximate distribution in the low signal-to-noise ratio (SNR) regime with the use of the central limit theorem, are obtained. Theoretical analysis is then performed and our results show that the performance loss of the proposed detector is approximately $2$ dB ($\pi/2$) compared to detectors employing $\infty$-bit ADCs when SNR is low. This loss can be compensated for by using approximately $2.47$ ($\pi^2/4$) times more samples. In addition, we unveil that the efficiency of incoherent accumulation in one-bit detection is the square root of that of coherent accumulation. Simulation results corroborate the correctness of our theoretical calculations.

One-Bit Covariance Reconstruction with Non-zero Thresholds: Algorithm and Performance Analysis

Covariance matrix reconstruction is a topic of great significance in the field of one-bit signal processing and has numerous practical applications. Despite its importance, the conventional arcsine law with zero threshold is incapable of recovering the diagonal elements of the covariance matrix. To address this limitation, recent studies have proposed the use of non-zero clipping thresholds. However, the relationship between the estimation error and the sampling threshold is not yet known. In this paper, we undertake an analysis of the mean squared error by computing the Fisher information matrix for a given threshold. Our results reveal that the optimal threshold can vary considerably, depending on the variances and correlation coefficients. As a result, it is inappropriate to use a constant threshold to encompass parameters that vary widely. To mitigate this issue, we present a recovery scheme that incorporates time-varying thresholds. Our approach differs from existing methods in that it utilizes the exact values of the threshold, rather than its statistical properties, to enhance the estimation performance. Our simulations, including the direction-of-arrival estimation problem, demonstrate the efficacy of the developed scheme, especially in complex scenarios where the covariance elements are widely separated.

Graph-signal Reconstruction and Blind Deconvolution for Structured Inputs

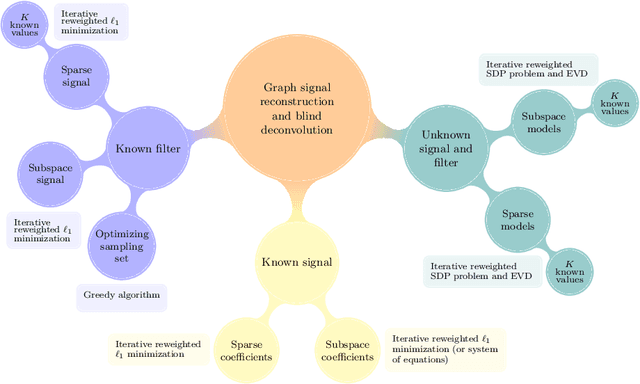
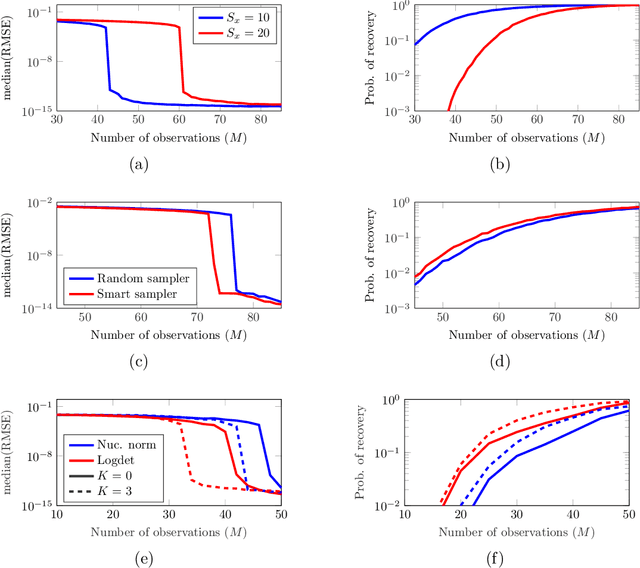
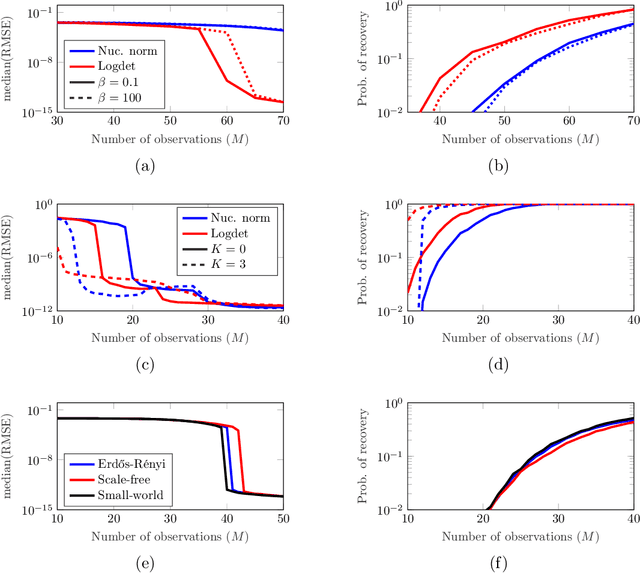
Key to successfully deal with complex contemporary datasets is the development of tractable models that account for the irregular structure of the information at hand. This paper provides a comprehensive and unifying view of several sampling, reconstruction, and recovery problems for signals defined on irregular domains that can be accurately represented by a graph. The workhorse assumption is that the (partially) observed signals can be modeled as the output of a graph filter to a structured (parsimonious) input graph signal. When either the input or the filter coefficients are known, this is tantamount to assuming that the signals of interest live on a subspace defined by the supporting graph. When neither is known, the model becomes bilinear. Upon imposing different priors and additional structure on either the input or the filter coefficients, a broad range of relevant problem formulations arise. The goal is then to leverage those priors, the shift operator of the supporting graph, and the samples of the signal of interest to recover: the signal at the non-sampled nodes (graph-signal interpolation), the input (deconvolution), the filter coefficients (system identification), or any combination thereof (blind deconvolution).

One-Bit Target Detection in Collocated MIMO Radar and Performance Degradation Analysis

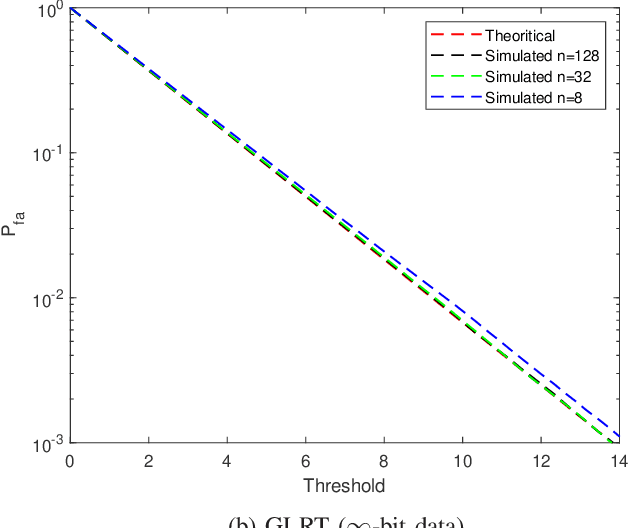
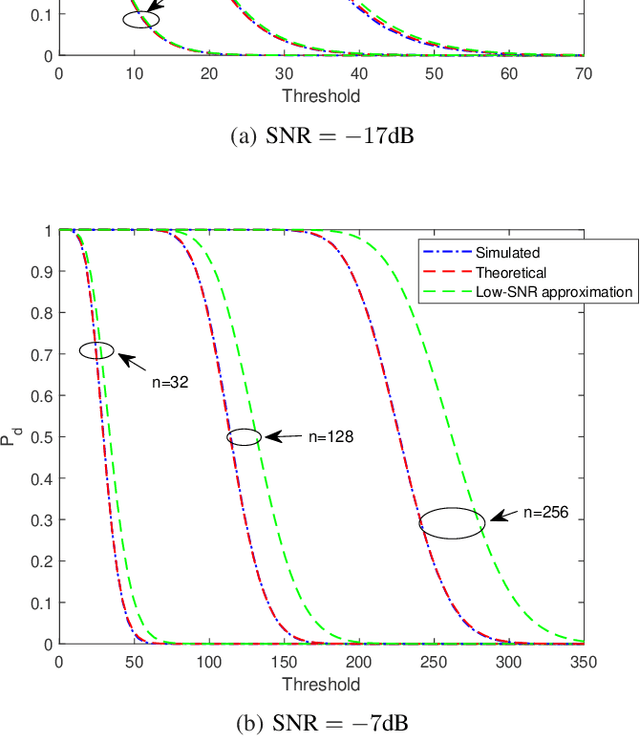
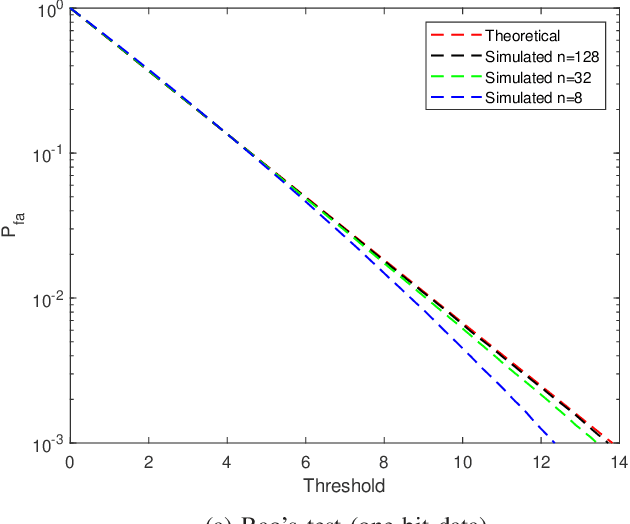
Target detection is an important problem in multiple-input multiple-output (MIMO) radar. Many existing target detection algorithms were proposed without taking into consideration the quantization error caused by analog-to-digital converters (ADCs). This paper addresses the problem of target detection for MIMO radar with one-bit ADCs and derives a Rao's test-based detector. The proposed method has several appealing features: 1) it is a closed-form detector; 2) it allows us to handle sign measurements straightforwardly; 3) there are closed-form approximations of the detector's distributions, which allow us to theoretically evaluate its performance. Moreover, the closed-form distributions allow us to study the performance degradation due to the one-bit ADCs, yielding an approximate $2$ dB loss in the low-signal-to-noise-ratio (SNR) regime compared to $\infty$-bit ADCs. Simulation results are included to showcase the advantage of the proposed detector and validate the accuracy of the theoretical results.

Continual Learning for Infinite Hierarchical Change-Point Detection

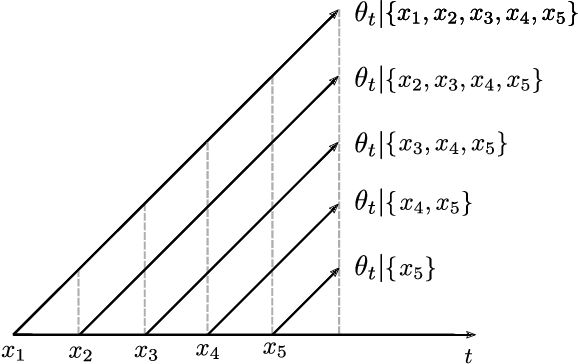
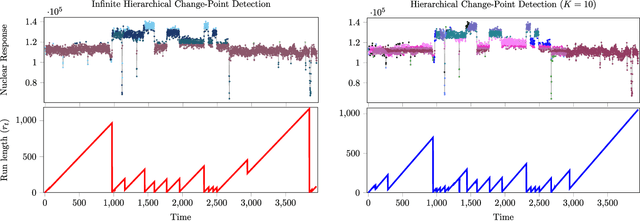
Change-point detection (CPD) aims to locate abrupt transitions in the generative model of a sequence of observations. When Bayesian methods are considered, the standard practice is to infer the posterior distribution of the change-point locations. However, for complex models (high-dimensional or heterogeneous), it is not possible to perform reliable detection. To circumvent this problem, we propose to use a hierarchical model, which yields observations that belong to a lower-dimensional manifold. Concretely, we consider a latent-class model with an unbounded number of categories, which is based on the chinese-restaurant process (CRP). For this model we derive a continual learning mechanism that is based on the sequential construction of the CRP and the expectation-maximization (EM) algorithm with a stochastic maximization step. Our results show that the proposed method is able to recursively infer the number of underlying latent classes and perform CPD in a reliable manner.

Change-Point Detection on Hierarchical Circadian Models

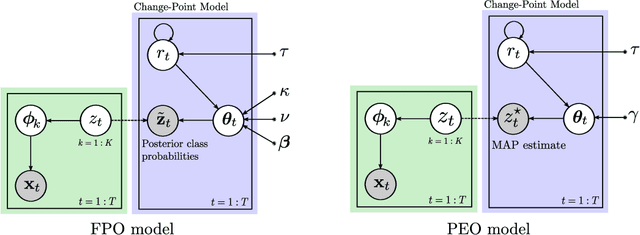
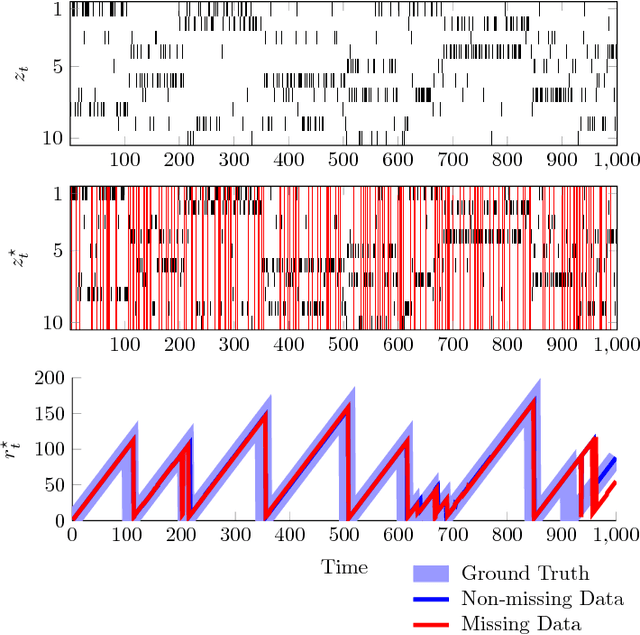
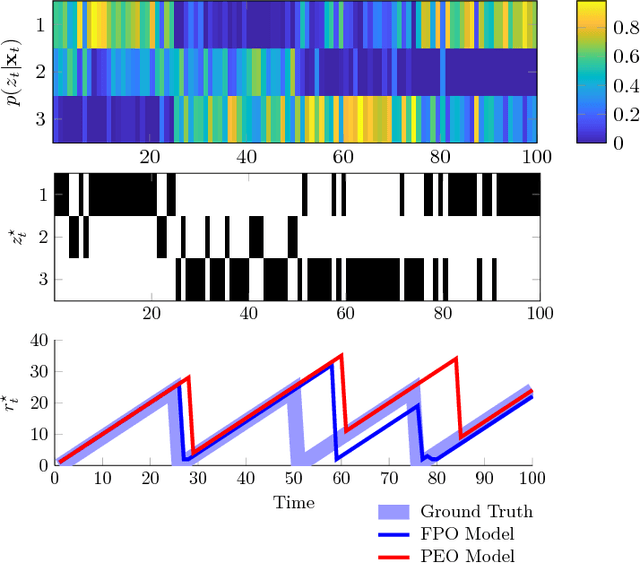
This paper addresses the problem of change-point detection on sequences of high-dimensional and heterogeneous observations, which also possess a periodic temporal structure. Due to the dimensionality problem, when the time between change-points is on the order of the dimension of the model parameters, drifts in the underlying distribution can be misidentified as changes. To overcome this limitation we assume that the observations lie in a lower dimensional manifold that admits a latent variable representation. In particular, we propose a hierarchical model that is computationally feasible, widely applicable to heterogeneous data and robust to missing instances. Additionally, to deal with the observations' periodic dependencies, we employ a circadian model where the data periodicity is captured by non-stationary covariance functions. We validate the proposed technique on synthetic examples and we demonstrate its utility in the detection of changes for human behavior characterization.