Multi-Channel Factor Analysis: Identifiability and Asymptotics

Recent work by Ram\'irez et al. [2] has introduced Multi-Channel Factor Analysis (MFA) as an extension of factor analysis to multi-channel data that allows for latent factors common to all channels as well as factors specific to each channel. This paper validates the MFA covariance model and analyzes the statistical properties of the MFA estimators. In particular, a thorough investigation of model identifiability under varying latent factor structures is conducted, and sufficient conditions for generic global identifiability of MFA are obtained. The development of these identifiability conditions enables asymptotic analysis of estimators obtained by maximizing a Gaussian likelihood, which are shown to be consistent and asymptotically normal even under misspecification of the latent factor distribution.

First-Order Statistical Framework for Multi-Channel Passive Detection

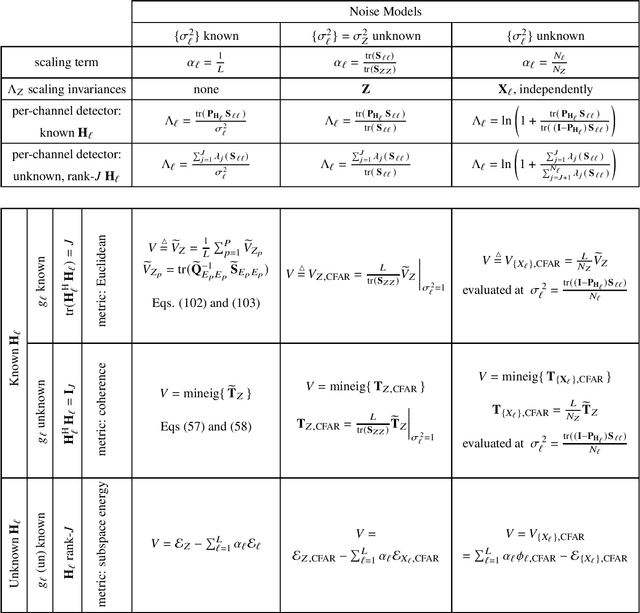
In this paper we establish a general first-order statistical framework for the detection of a common signal impinging on spatially distributed receivers. We consider three types of channel models: 1) the propagation channel is completely known, 2) the propagation is known but channel gains are unknown, and 3) the propagation channel is unknown. For each problem, we address the cases of a) known noise variances, b) common but unknown noise variances, and c) different and unknown noise variances. For all 9 cases, we establish generalized-likelihood-ratio (GLR) detectors, and show that each one can be decomposed into two terms. The first term is a weighted combination of the GLR detectors that arise from considering each channel separately. This result is then modified by a fusion or cross-validation term, which expresses the level of confidence that the single-channel detectors have detected a common source. Of particular note are the constant false-alarm rate (CFAR) detectors that allow for scale-invariant detection in multiple channels with different noise powers.