One-Bit Target Detection in Collocated MIMO Radar and Performance Degradation Analysis

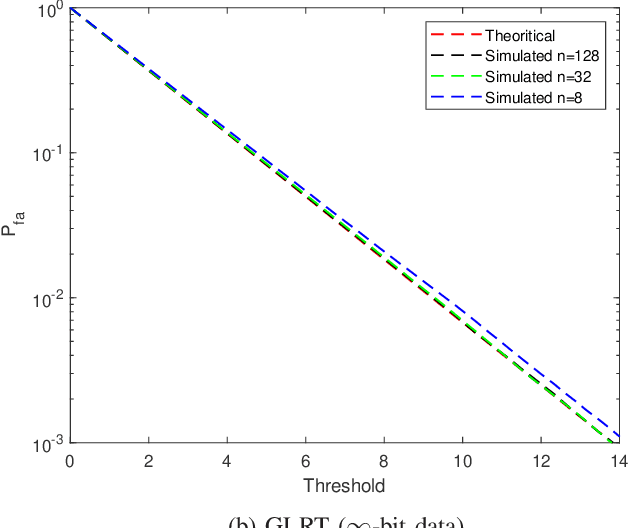
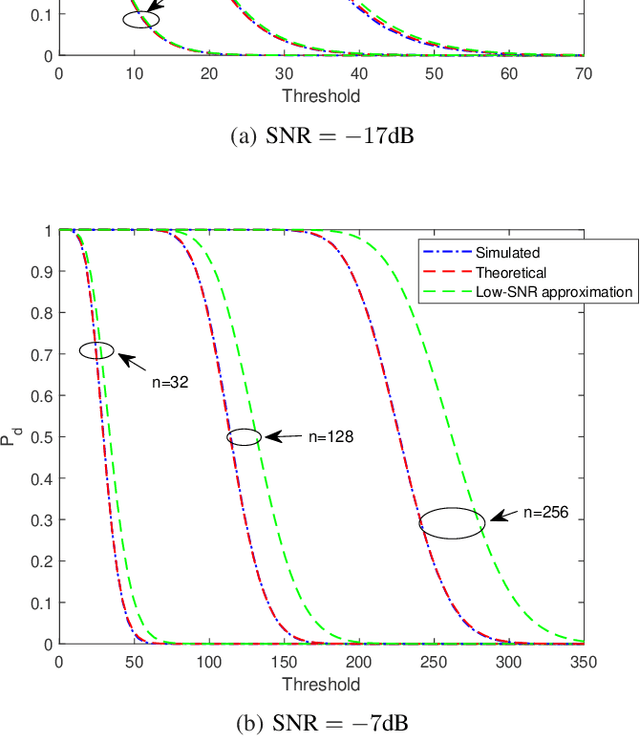
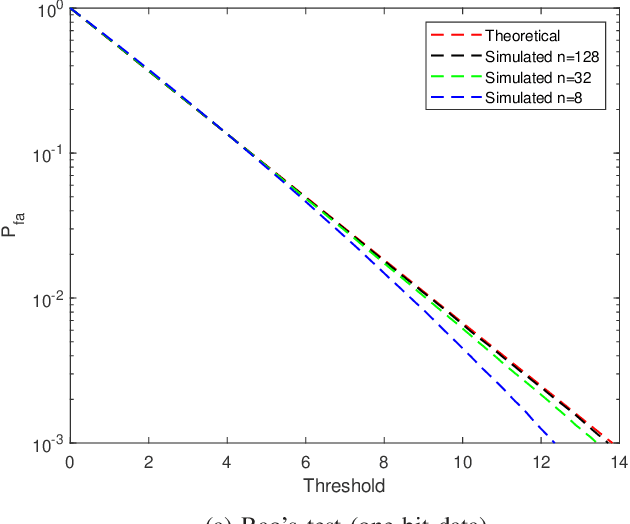
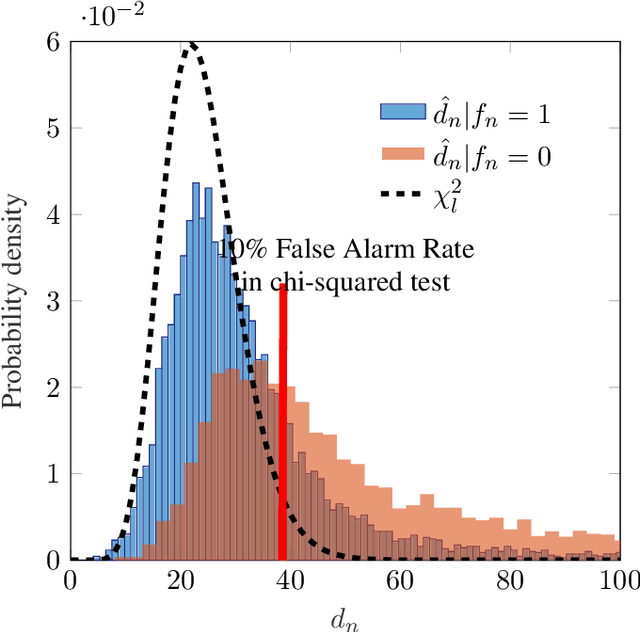
Target detection is an important problem in multiple-input multiple-output (MIMO) radar. Many existing target detection algorithms were proposed without taking into consideration the quantization error caused by analog-to-digital converters (ADCs). This paper addresses the problem of target detection for MIMO radar with one-bit ADCs and derives a Rao's test-based detector. The proposed method has several appealing features: 1) it is a closed-form detector; 2) it allows us to handle sign measurements straightforwardly; 3) there are closed-form approximations of the detector's distributions, which allow us to theoretically evaluate its performance. Moreover, the closed-form distributions allow us to study the performance degradation due to the one-bit ADCs, yielding an approximate $2$ dB loss in the low-signal-to-noise-ratio (SNR) regime compared to $\infty$-bit ADCs. Simulation results are included to showcase the advantage of the proposed detector and validate the accuracy of the theoretical results.

Procrustes registration of two-dimensional statistical shape models without correspondences

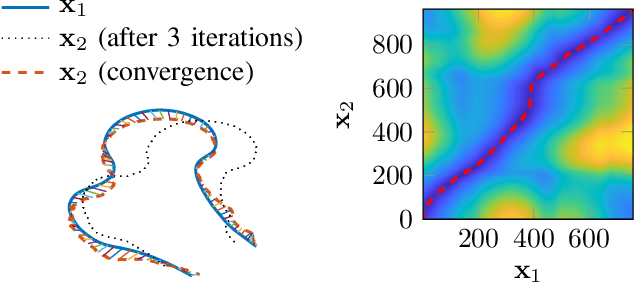
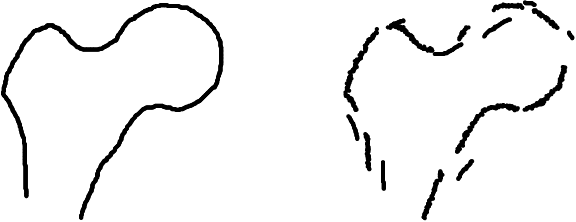
Statistical shape models are a useful tool in image processing and computer vision. A Procrustres registration of the contours of the same shape is typically perform to align the training samples to learn the statistical shape model. A Procrustes registration between two contours with known correspondences is straightforward. However, these correspondences are not generally available. Manually placed landmarks are often used for correspondence in the design of statistical shape models. However, determining manual landmarks on the contours is time-consuming and often error-prone. One solution to simultaneously find correspondence and registration is the Iterative Closest Point (ICP) algorithm. However, ICP requires an initial position of the contours that is close to registration, and it is not robust against outliers. We propose a new strategy, based on Dynamic Time Warping, that efficiently solves the Procrustes registration problem without correspondences. We study the registration performance in a collection of different shape data sets and show that our technique outperforms competing techniques based on the ICP approach. Our strategy is applied to an ensemble of contours of the same shape as an extension of the generalized Procrustes analysis accounting for a lack of correspondence.

Deep Morphing: Detecting bone structures in fluoroscopic X-ray images with prior knowledge

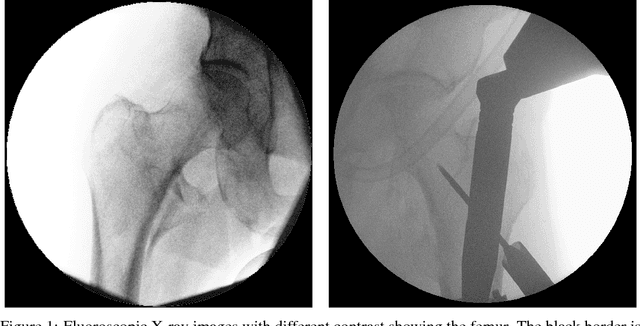
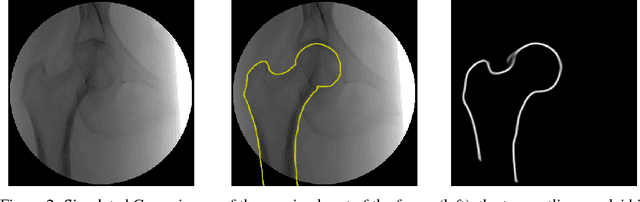
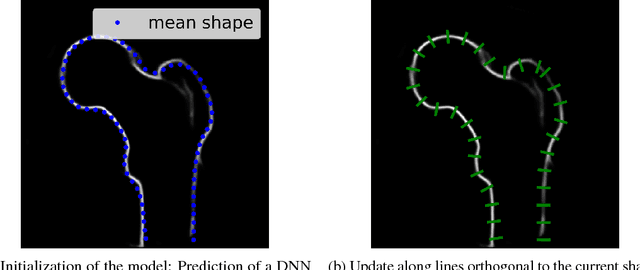
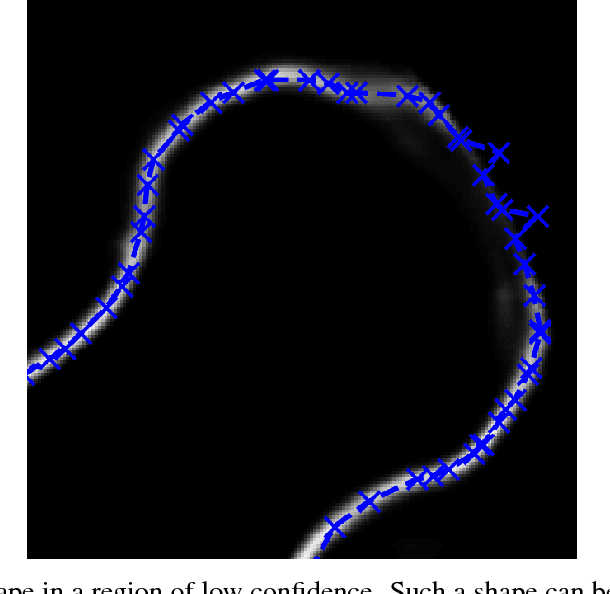
We propose approaches based on deep learning to localize objects in images when only a small training dataset is available and the images have low quality. That applies to many problems in medical image processing, and in particular to the analysis of fluoroscopic (low-dose) X-ray images, where the images have low contrast. We solve the problem by incorporating high-level information about the objects, which could be a simple geometrical model, like a circular outline, or a more complex statistical model. A simple geometrical representation can sufficiently describe some objects and only requires minimal labeling. Statistical shape models can be used to represent more complex objects. We propose computationally efficient two-stage approaches, which we call deep morphing, for both representations by fitting the representation to the output of a deep segmentation network.

Model-order selection in statistical shape models

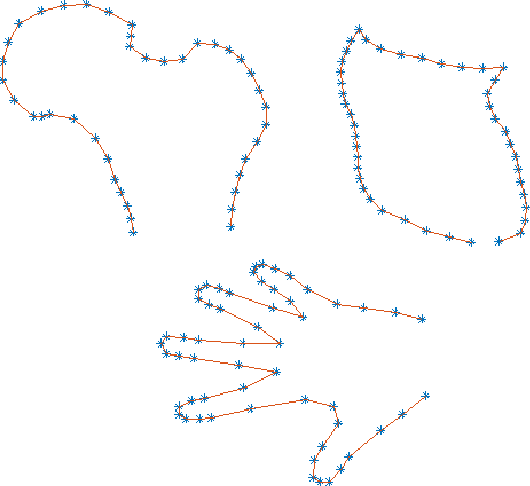
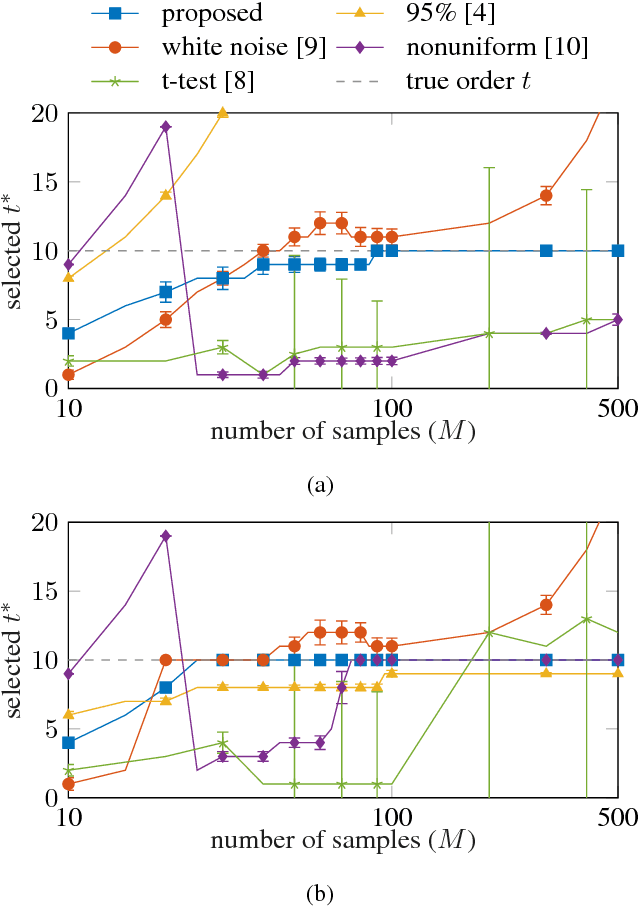
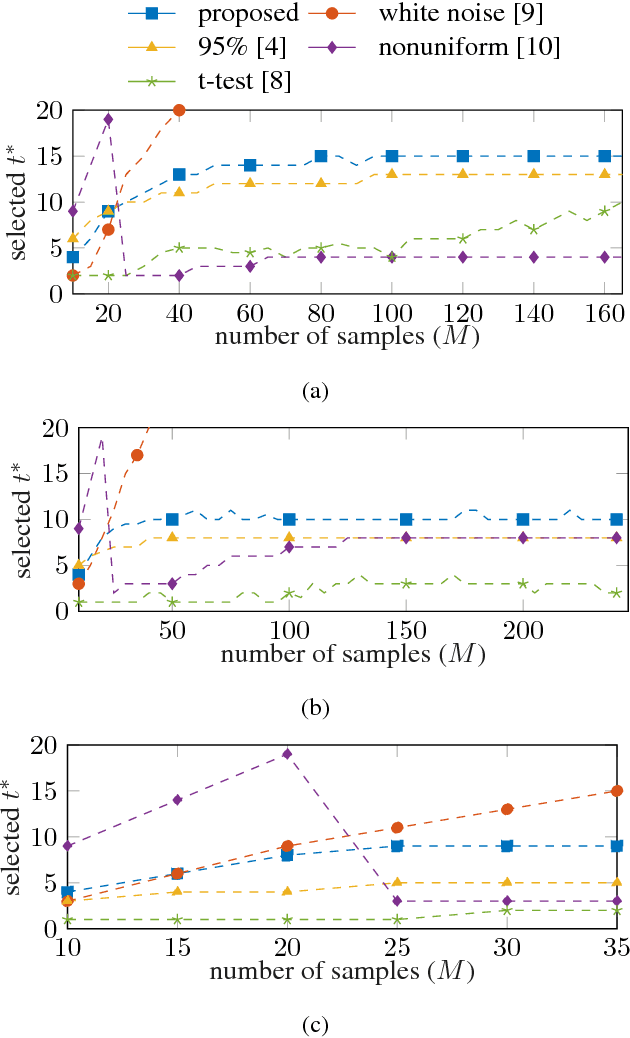
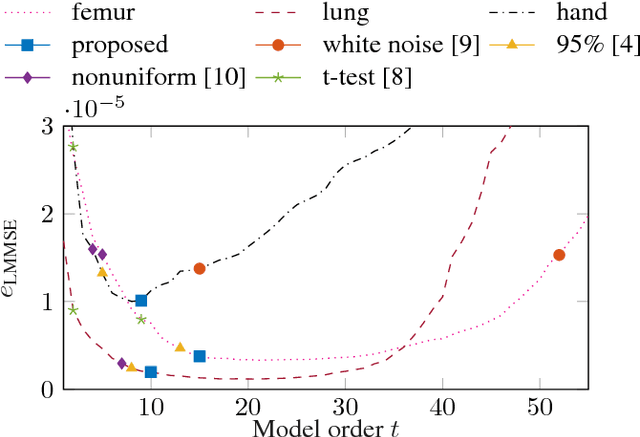
Statistical shape models enhance machine learning algorithms providing prior information about deformation. A Point Distribution Model (PDM) is a popular landmark-based statistical shape model for segmentation. It requires choosing a model order, which determines how much of the variation seen in the training data is accounted for by the PDM. A good choice of the model order depends on the number of training samples and the noise level in the training data set. Yet the most common approach for choosing the model order simply keeps a predetermined percentage of the total shape variation. In this paper, we present a technique for choosing the model order based on information-theoretic criteria, and we show empirical evidence that the model order chosen by this technique provides a good trade-off between over- and underfitting.

A weighting strategy for Active Shape Models

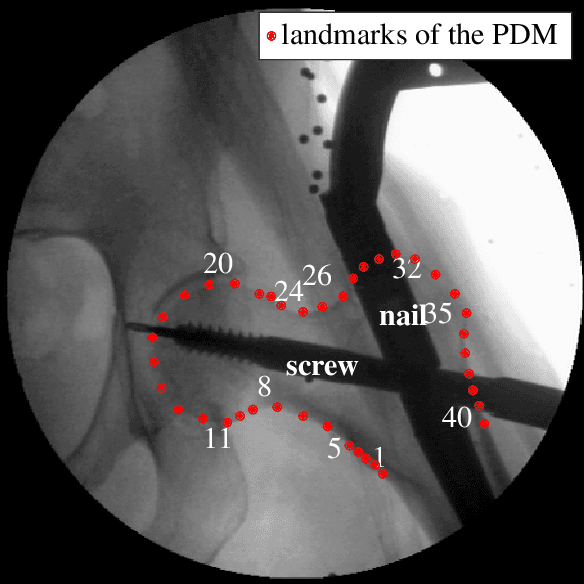
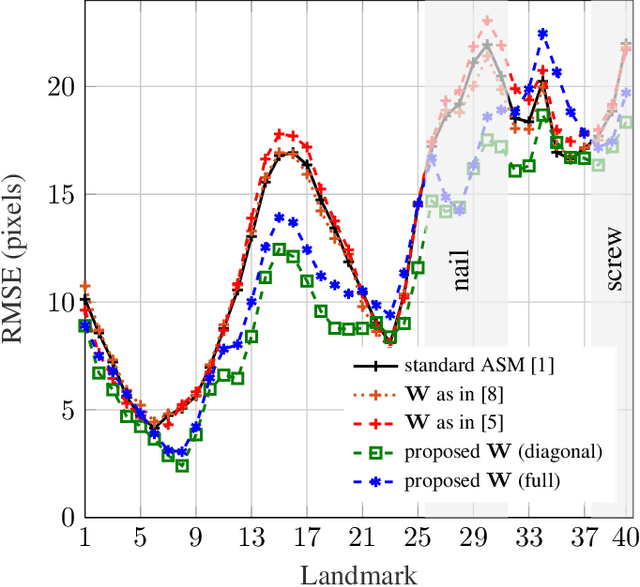
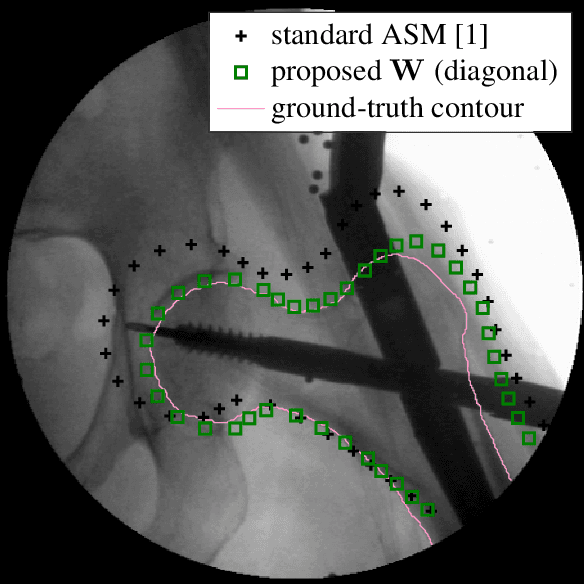
Active Shape Models (ASM) are an iterative segmentation technique to find a landmark-based contour of an object. In each iteration, a least-squares fit of a plausible shape to some detected target landmarks is determined. Finding these targets is a critical step: some landmarks are more reliably detected than others, and some landmarks may not be within the field of view of their detectors. To add robustness while preserving simplicity at the same time, a generalized least-squares approach can be used, where a weighting matrix incorporates reliability information about the landmarks. We propose a strategy to choose this matrix, based on the covariance of empirically determined residuals of the fit. We perform a further step to determine whether the target landmarks are within the range of their detectors. We evaluate our strategy on fluoroscopic X-ray images to segment the femur. We show that our technique outperforms the standard ASM as well as other more heuristic weighted least-squares strategies.

Detecting Directionality in Random Fields Using the Monogenic Signal

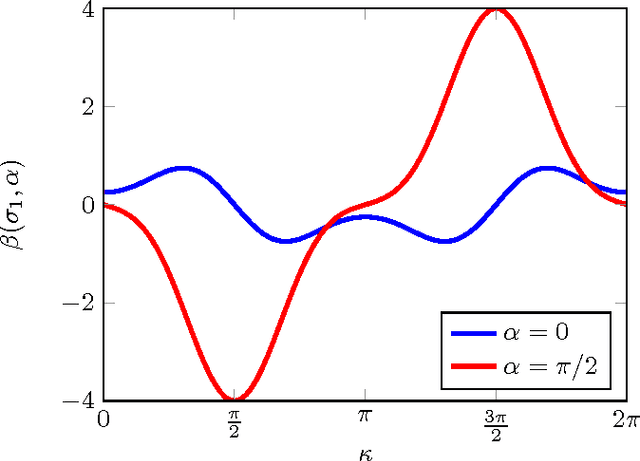
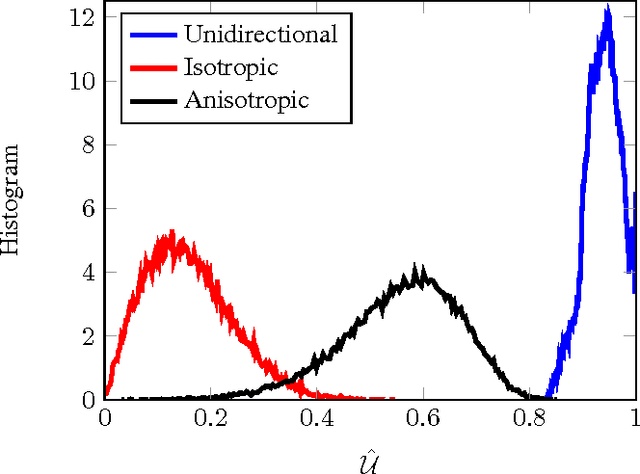
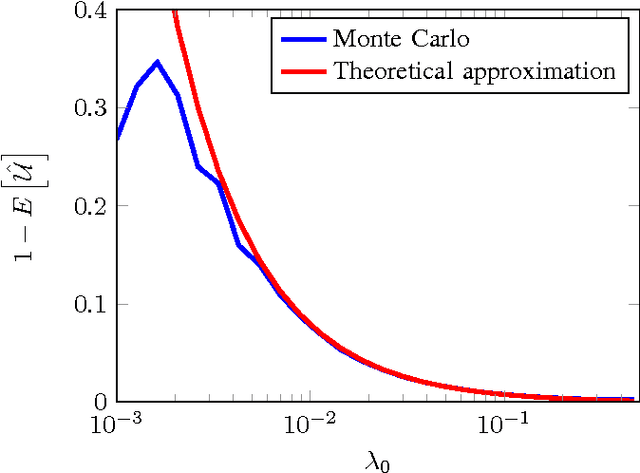
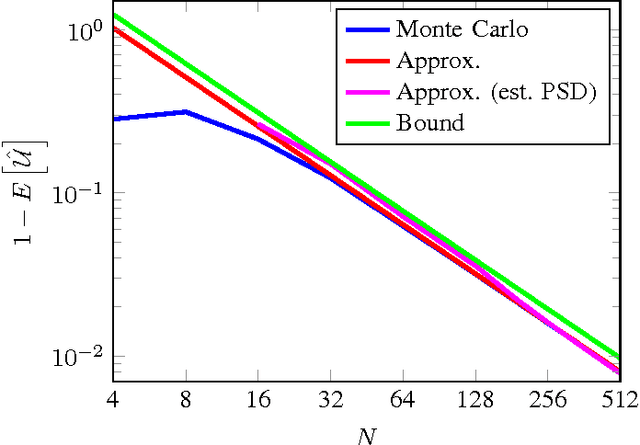
Detecting and analyzing directional structures in images is important in many applications since one-dimensional patterns often correspond to important features such as object contours or trajectories. Classifying a structure as directional or non-directional requires a measure to quantify the degree of directionality and a threshold, which needs to be chosen based on the statistics of the image. In order to do this, we model the image as a random field. So far, little research has been performed on analyzing directionality in random fields. In this paper, we propose a measure to quantify the degree of directionality based on the random monogenic signal, which enables a unique decomposition of a 2D signal into local amplitude, local orientation, and local phase. We investigate the second-order statistical properties of the monogenic signal for isotropic, anisotropic, and unidirectional random fields. We analyze our measure of directionality for finite-size sample images, and determine a threshold to distinguish between unidirectional and non-unidirectional random fields, which allows the automatic classification of images.