Sofia Olhede
Tractably Modelling Dependence in Networks Beyond Exchangeability
Jul 28, 2020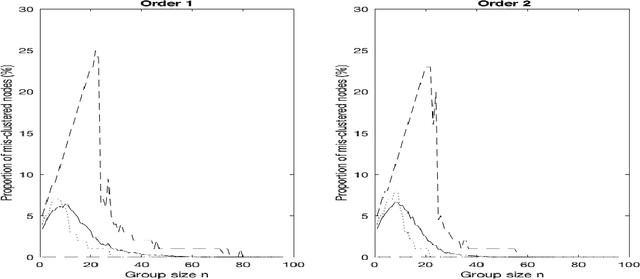


Abstract:We propose a general framework for modelling network data that is designed to describe aspects of non-exchangeable networks. Conditional on latent (unobserved) variables, the edges of the network are generated by their finite growth history (with latent orders) while the marginal probabilities of the adjacency matrix are modeled by a generalization of a graph limit function (or a graphon). In particular, we study the estimation, clustering and degree behavior of the network in our setting. We determine (i) the minimax estimator of a composite graphon with respect to squared error loss; (ii) that spectral clustering is able to consistently detect the latent membership when the block-wise constant composite graphon is considered under additional conditions; and (iii) we are able to construct models with heavy-tailed empirical degrees under specific scenarios and parameter choices. This explores why and under which general conditions non-exchangeable network data can be described by a stochastic block model. The new modelling framework is able to capture empirically important characteristics of network data such as sparsity combined with heavy tailed degree distribution, and add understanding as to what generative mechanisms will make them arise. Keywords: statistical network analysis, exchangeable arrays, stochastic block model, nonlinear stochastic processes.
Detecting Directionality in Random Fields Using the Monogenic Signal
Jun 10, 2014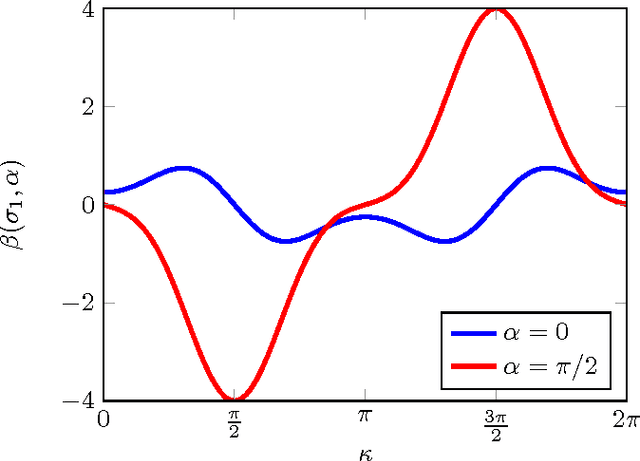
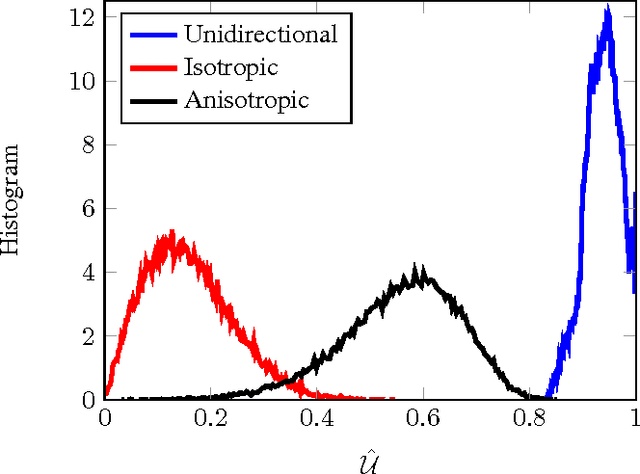
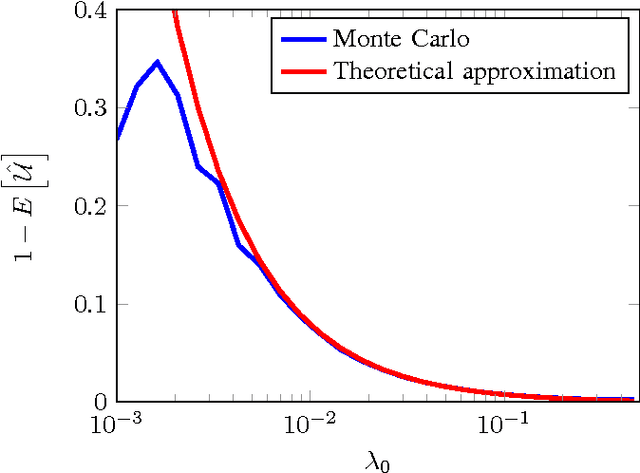
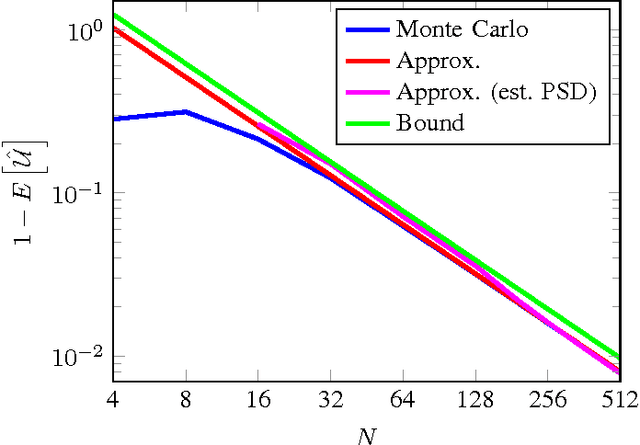
Abstract:Detecting and analyzing directional structures in images is important in many applications since one-dimensional patterns often correspond to important features such as object contours or trajectories. Classifying a structure as directional or non-directional requires a measure to quantify the degree of directionality and a threshold, which needs to be chosen based on the statistics of the image. In order to do this, we model the image as a random field. So far, little research has been performed on analyzing directionality in random fields. In this paper, we propose a measure to quantify the degree of directionality based on the random monogenic signal, which enables a unique decomposition of a 2D signal into local amplitude, local orientation, and local phase. We investigate the second-order statistical properties of the monogenic signal for isotropic, anisotropic, and unidirectional random fields. We analyze our measure of directionality for finite-size sample images, and determine a threshold to distinguish between unidirectional and non-unidirectional random fields, which allows the automatic classification of images.
Multiscale Inference for High-Frequency Data
Apr 19, 2009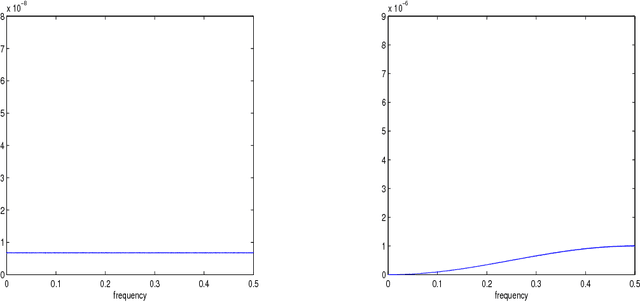
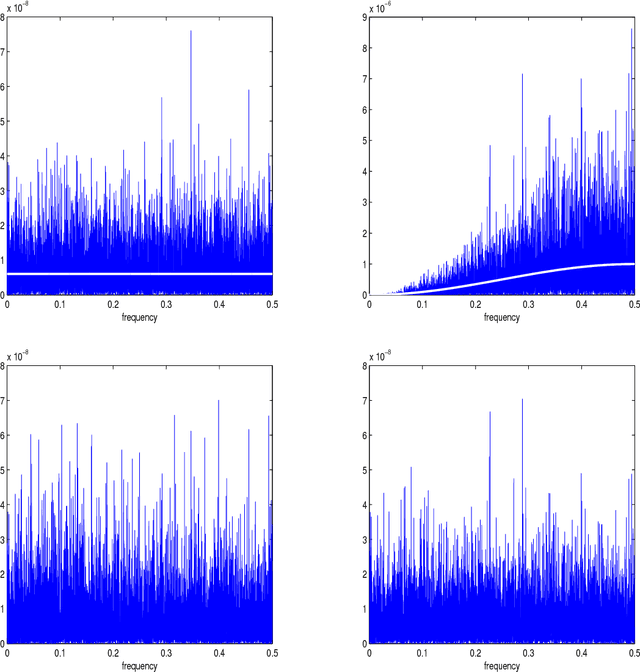
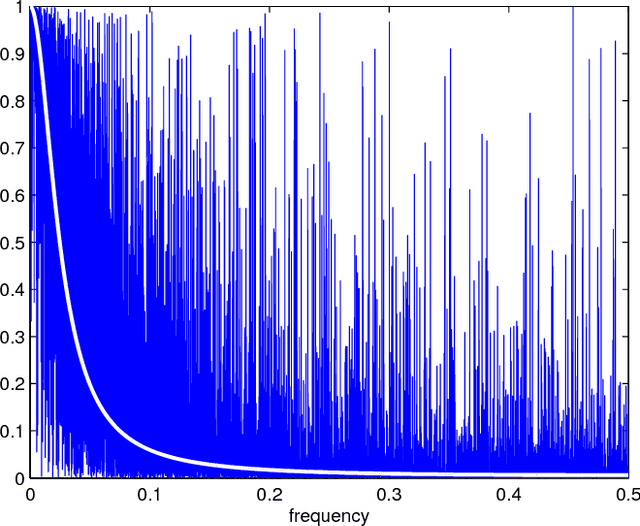
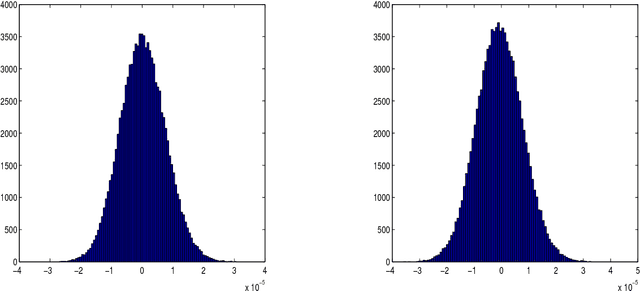
Abstract:This paper proposes a novel multiscale estimator for the integrated volatility of an Ito process, in the presence of market microstructure noise (observation error). The multiscale structure of the observed process is represented frequency-by-frequency and the concept of the multiscale ratio is introduced to quantify the bias in the realized integrated volatility due to the observation error. The multiscale ratio is estimated from a single sample path, and a frequency-by-frequency bias correction procedure is proposed, which simultaneously reduces variance. We extend the method to include correlated observation errors and provide the implied time domain form of the estimation procedure. The new method is implemented to estimate the integrated volatility for the Heston and other models, and the improved performance of our method over existing methods is illustrated by simulation studies.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge