Tractably Modelling Dependence in Networks Beyond Exchangeability
Paper and Code
Jul 28, 2020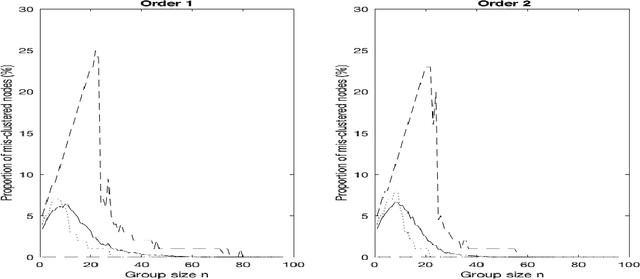


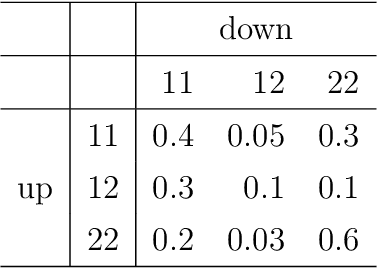
We propose a general framework for modelling network data that is designed to describe aspects of non-exchangeable networks. Conditional on latent (unobserved) variables, the edges of the network are generated by their finite growth history (with latent orders) while the marginal probabilities of the adjacency matrix are modeled by a generalization of a graph limit function (or a graphon). In particular, we study the estimation, clustering and degree behavior of the network in our setting. We determine (i) the minimax estimator of a composite graphon with respect to squared error loss; (ii) that spectral clustering is able to consistently detect the latent membership when the block-wise constant composite graphon is considered under additional conditions; and (iii) we are able to construct models with heavy-tailed empirical degrees under specific scenarios and parameter choices. This explores why and under which general conditions non-exchangeable network data can be described by a stochastic block model. The new modelling framework is able to capture empirically important characteristics of network data such as sparsity combined with heavy tailed degree distribution, and add understanding as to what generative mechanisms will make them arise. Keywords: statistical network analysis, exchangeable arrays, stochastic block model, nonlinear stochastic processes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge