Adam Sykulski
Multiscale Inference for High-Frequency Data
Apr 19, 2009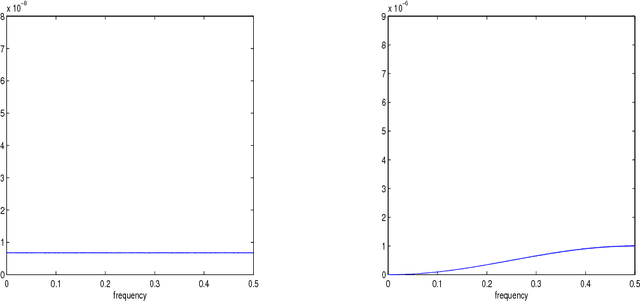
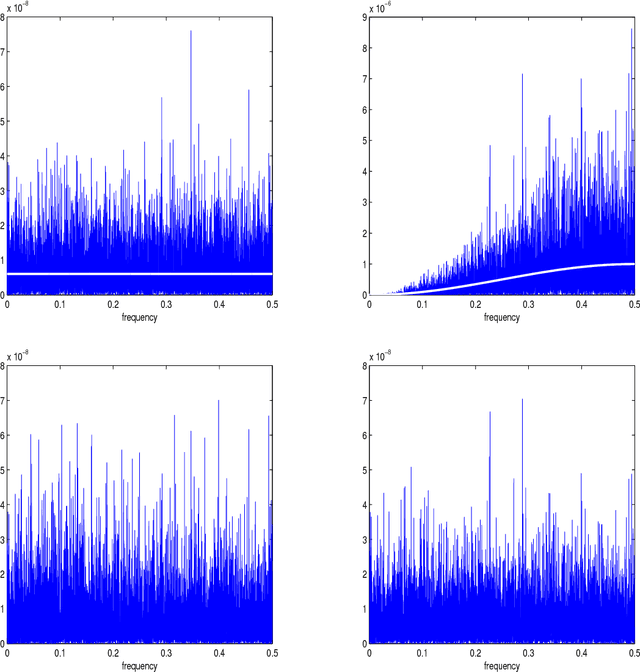
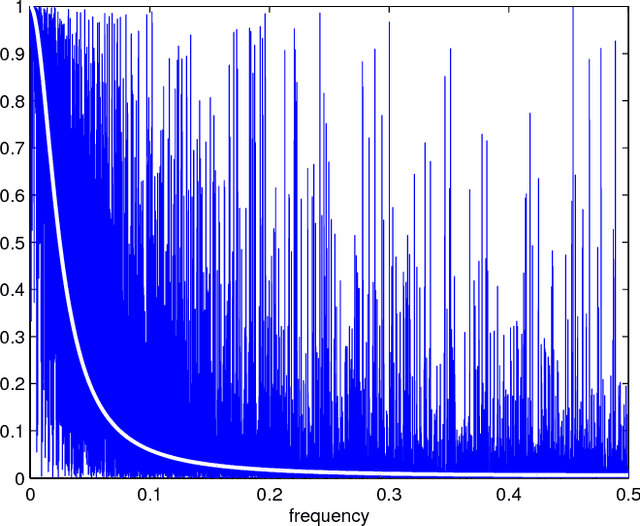
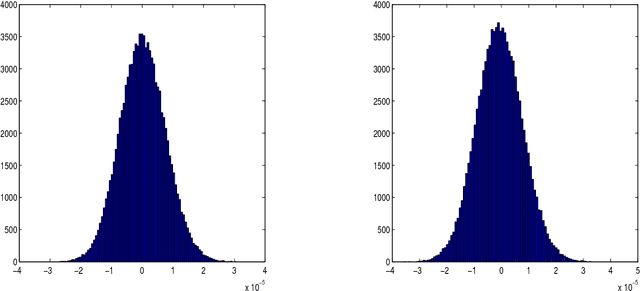
Abstract:This paper proposes a novel multiscale estimator for the integrated volatility of an Ito process, in the presence of market microstructure noise (observation error). The multiscale structure of the observed process is represented frequency-by-frequency and the concept of the multiscale ratio is introduced to quantify the bias in the realized integrated volatility due to the observation error. The multiscale ratio is estimated from a single sample path, and a frequency-by-frequency bias correction procedure is proposed, which simultaneously reduces variance. We extend the method to include correlated observation errors and provide the implied time domain form of the estimation procedure. The new method is implemented to estimate the integrated volatility for the Heston and other models, and the improved performance of our method over existing methods is illustrated by simulation studies.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge