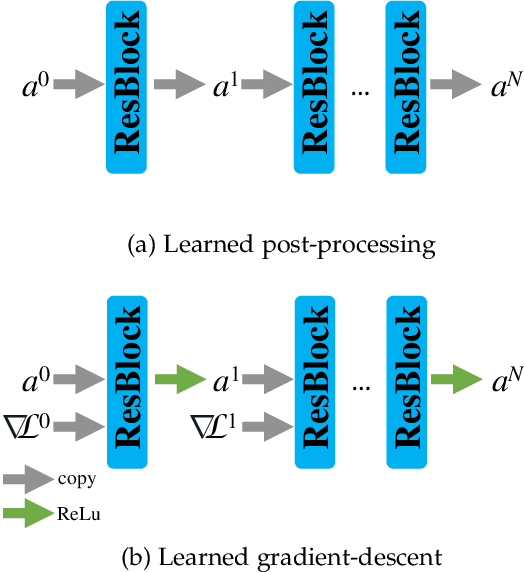
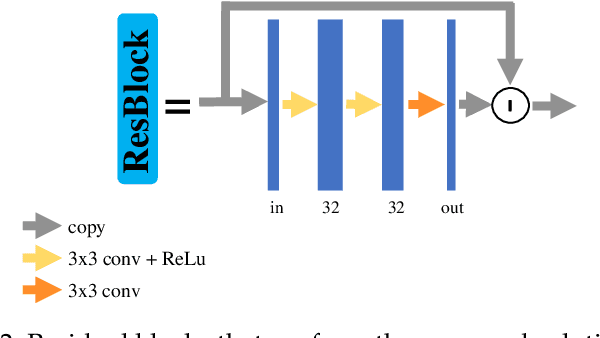
Deep Learning for Material Decomposition in Photon-Counting CT

Photon-counting CT (PCCT) offers improved diagnostic performance through better spatial and energy resolution, but developing high-quality image reconstruction methods that can deal with these large datasets is challenging. Model-based solutions incorporate models of the physical acquisition in order to reconstruct more accurate images, but are dependent on an accurate forward operator and present difficulties with finding good regularization. Another approach is deep-learning reconstruction, which has shown great promise in CT. However, fully data-driven solutions typically need large amounts of training data and lack interpretability. To combine the benefits of both methods, while minimizing their respective drawbacks, it is desirable to develop reconstruction algorithms that combine both model-based and data-driven approaches. In this work, we present a novel deep-learning solution for material decomposition in PCCT, based on an unrolled/unfolded iterative network. We evaluate two cases: a learned post-processing, which implicitly utilizes model knowledge, and a learned gradient-descent, which has explicit model-based components in the architecture. With our proposed techniques, we solve a challenging PCCT simulation case: three-material decomposition in abdomen imaging with low dose, iodine contrast, and a very small training sample support. In this scenario, our approach outperforms a maximum likelihood estimation, a variational method, as well as a fully-learned network.

Procrustes registration of two-dimensional statistical shape models without correspondences

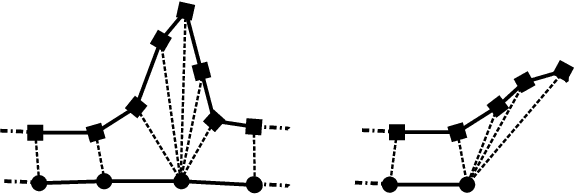
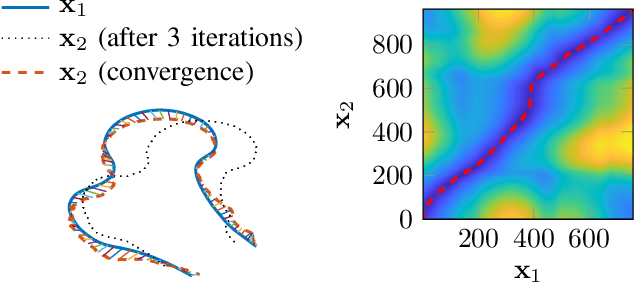
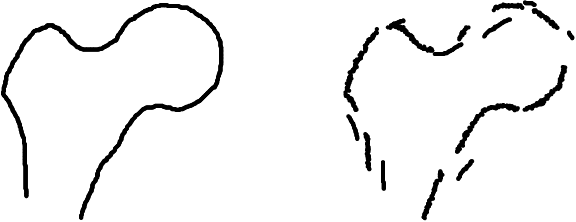
Statistical shape models are a useful tool in image processing and computer vision. A Procrustres registration of the contours of the same shape is typically perform to align the training samples to learn the statistical shape model. A Procrustes registration between two contours with known correspondences is straightforward. However, these correspondences are not generally available. Manually placed landmarks are often used for correspondence in the design of statistical shape models. However, determining manual landmarks on the contours is time-consuming and often error-prone. One solution to simultaneously find correspondence and registration is the Iterative Closest Point (ICP) algorithm. However, ICP requires an initial position of the contours that is close to registration, and it is not robust against outliers. We propose a new strategy, based on Dynamic Time Warping, that efficiently solves the Procrustes registration problem without correspondences. We study the registration performance in a collection of different shape data sets and show that our technique outperforms competing techniques based on the ICP approach. Our strategy is applied to an ensemble of contours of the same shape as an extension of the generalized Procrustes analysis accounting for a lack of correspondence.

Model-order selection in statistical shape models

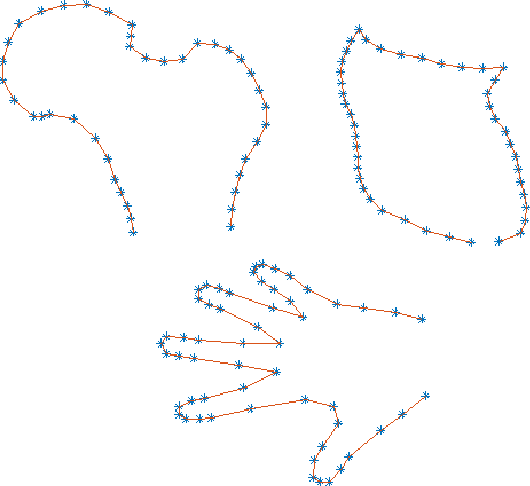
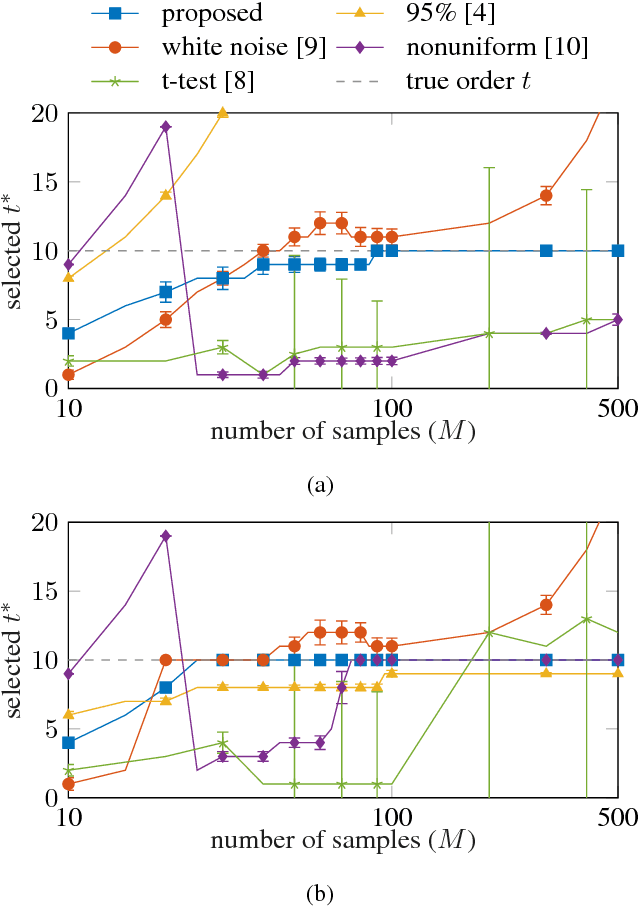
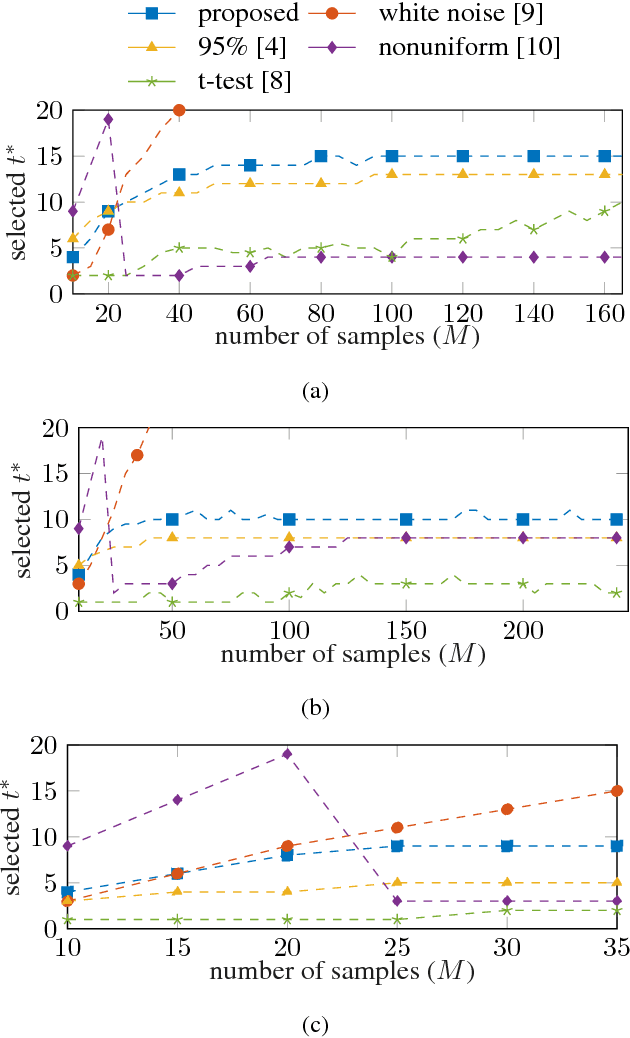
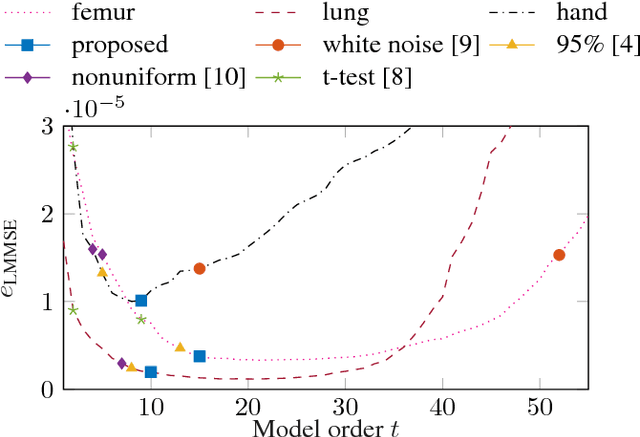
Statistical shape models enhance machine learning algorithms providing prior information about deformation. A Point Distribution Model (PDM) is a popular landmark-based statistical shape model for segmentation. It requires choosing a model order, which determines how much of the variation seen in the training data is accounted for by the PDM. A good choice of the model order depends on the number of training samples and the noise level in the training data set. Yet the most common approach for choosing the model order simply keeps a predetermined percentage of the total shape variation. In this paper, we present a technique for choosing the model order based on information-theoretic criteria, and we show empirical evidence that the model order chosen by this technique provides a good trade-off between over- and underfitting.

A weighting strategy for Active Shape Models

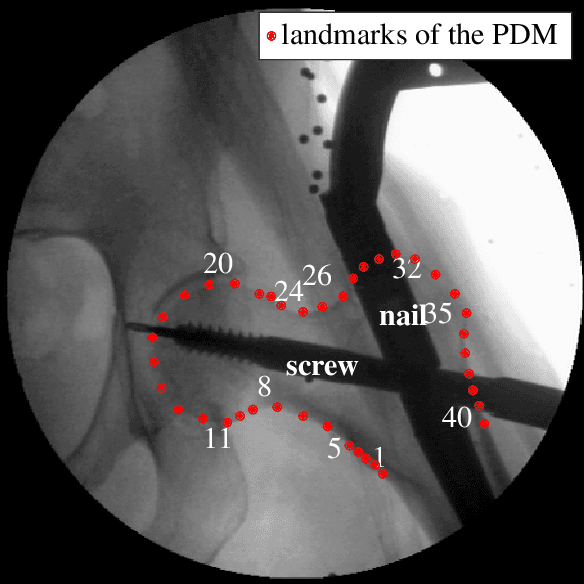
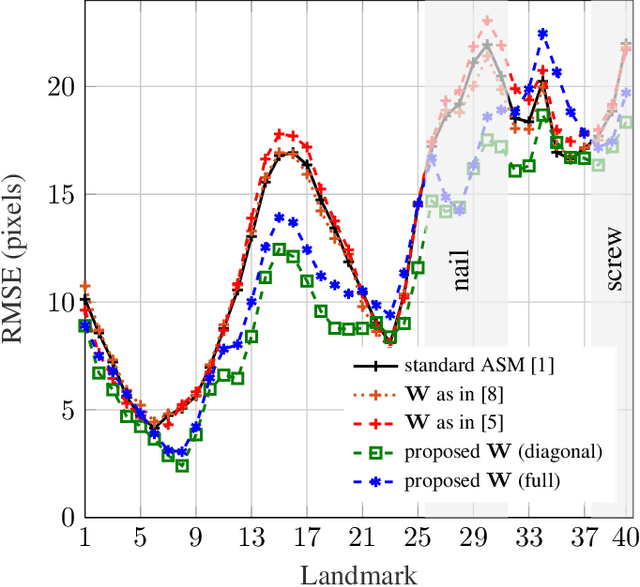
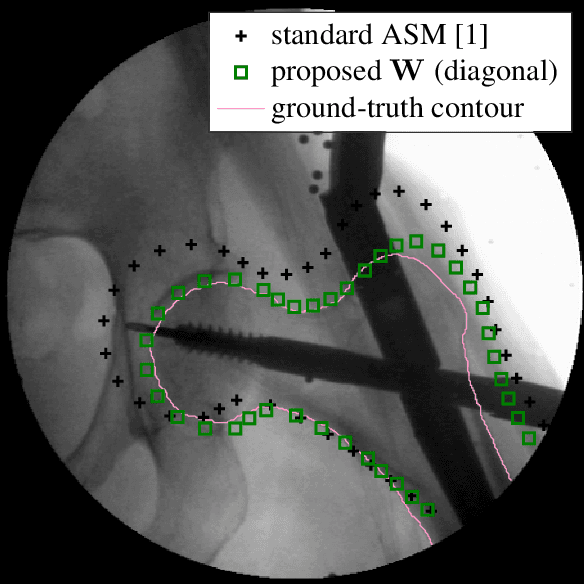
Active Shape Models (ASM) are an iterative segmentation technique to find a landmark-based contour of an object. In each iteration, a least-squares fit of a plausible shape to some detected target landmarks is determined. Finding these targets is a critical step: some landmarks are more reliably detected than others, and some landmarks may not be within the field of view of their detectors. To add robustness while preserving simplicity at the same time, a generalized least-squares approach can be used, where a weighting matrix incorporates reliability information about the landmarks. We propose a strategy to choose this matrix, based on the covariance of empirically determined residuals of the fit. We perform a further step to determine whether the target landmarks are within the range of their detectors. We evaluate our strategy on fluoroscopic X-ray images to segment the femur. We show that our technique outperforms the standard ASM as well as other more heuristic weighted least-squares strategies.