Change-Point Detection on Hierarchical Circadian Models

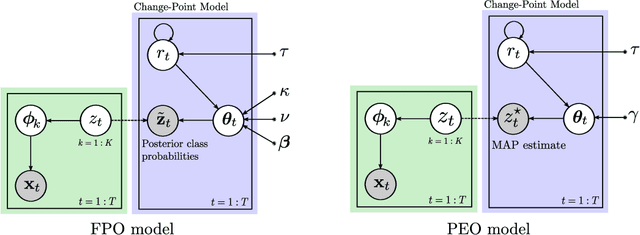
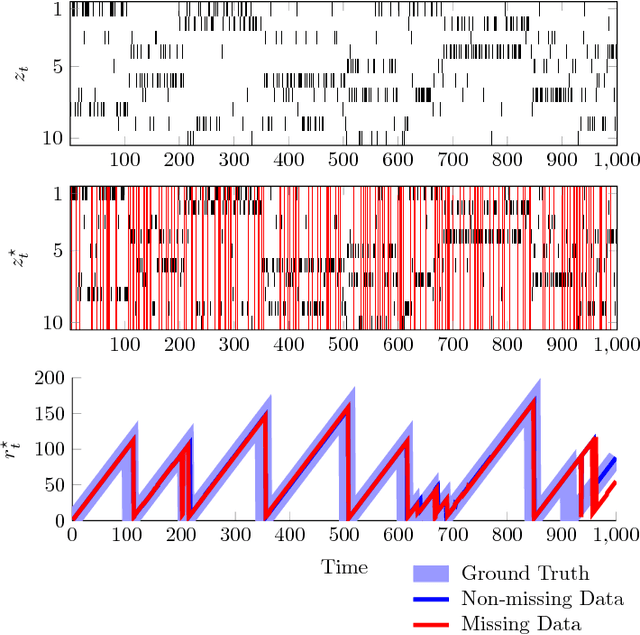
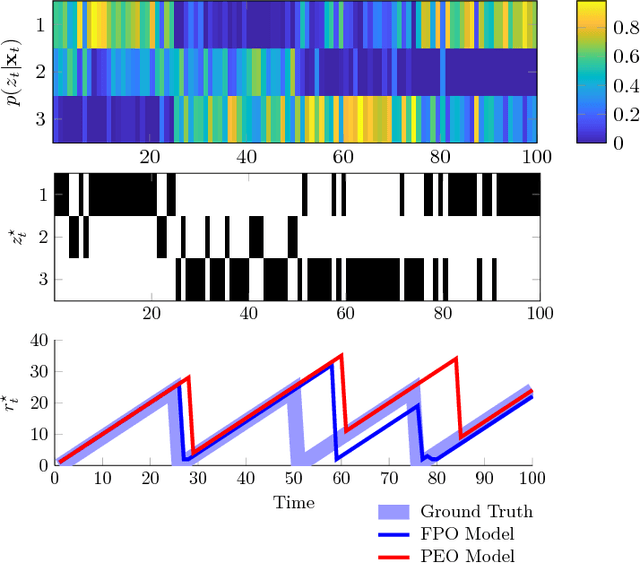
This paper addresses the problem of change-point detection on sequences of high-dimensional and heterogeneous observations, which also possess a periodic temporal structure. Due to the dimensionality problem, when the time between change-points is on the order of the dimension of the model parameters, drifts in the underlying distribution can be misidentified as changes. To overcome this limitation we assume that the observations lie in a lower dimensional manifold that admits a latent variable representation. In particular, we propose a hierarchical model that is computationally feasible, widely applicable to heterogeneous data and robust to missing instances. Additionally, to deal with the observations' periodic dependencies, we employ a circadian model where the data periodicity is captured by non-stationary covariance functions. We validate the proposed technique on synthetic examples and we demonstrate its utility in the detection of changes for human behavior characterization.