Passive detection of a random signal common to multi-sensor reference and surveillance arrays

This paper addresses the passive detection of a common rank-one subspace signal received in two multi-sensor arrays. We consider the case of a one-antenna transmitter sending a common Gaussian signal, independent Gaussian noises with arbitrary spatial covariance, and known channel subspaces. The detector derived in this paper is a generalized likelihood ratio (GLR) test. For all but one of the unknown parameters, it is possible to find closed-form maximum likelihood (ML) estimator functions. We can further compress the likelihood to only an unknown vector whose ML estimate requires maximizing a product of ratios in quadratic forms, which is carried out using a trust-region algorithm. We propose two approximations of the GLR that do not require any numerical optimization: one based on a sample-based estimator of the unknown parameter whose ML estimate cannot be obtained in closed-form, and one derived under low-SNR conditions. Notably, all the detectors are scale-invariant, and the approximations are functions of beamformed data. However, they are not GLRTs for data that has been pre-processed with a beamformer, a point that is elaborated in the paper. These detectors outperform previously published correlation detectors on simulated data, in many cases quite significantly. Moreover, performance results quantify the performance gains over detectors that assume only the dimension of the subspace to be known.

A Unified Theory of Adaptive Subspace Detection. Part II: Numerical Examples

This paper is devoted to the performance analysis of the detectors proposed in the companion paper where a comprehensive design framework is presented for the adaptive detection of subspace signals. The framework addresses four variations on subspace detection: the subspace may be known or known only by its dimension; consecutive visits to the subspace may be unconstrained or they may be constrained by a prior probability distribution. In this paper, Monte Carlo simulations are used to compare the generalized likelihood ratio (GLR) detectors derived in [1] with estimate-and-plug (EP) approximations of the GLR detectors. Remarkably, the EP approximations appear here for the first time (at least to the best of the authors' knowledge). The numerical examples indicate that GLR detectors are effective for the detection of partially-known signals affected by inherent uncertainties due to the system or the operating environment. In particular, if the signal subspace is known, GLR detectors tend to outperform EP detectors. If, instead, the signal subspace is known only by its dimension, the performance of GLR and EP detectors is very similar.

Testing for Causal Influence using a Partial Coherence Statistic

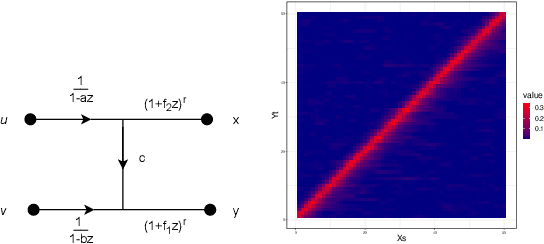
In this paper we explore partial coherence as a tool for evaluating causal influence of one signal sequence on another. In some cases the signal sequence is sampled from a time- or space-series. The key idea is to establish a connection between questions of causality and questions of partial coherence. Once this connection is established, then a scale-invariant partial coherence statistic is used to resolve the question of causality. This coherence statistic is shown to be a likelihood ratio, and its null distribution is shown to be a Wilks Lambda. It may be computed from a composite covariance matrix or from its inverse, the information matrix. Numerical experiments demonstrate the application of partial coherence to the resolution of causality. Importantly, the method is model-free, depending on no generative model for causality.

A Unified Theory of Adaptive Subspace Detection. Part I: Detector Designs

This paper addresses the problem of detecting multidimensional subspace signals, which model range-spread targets, in noise of unknown covariance. It is assumed that a primary channel of measurements, possibly consisting of signal plus noise, is augmented with a secondary channel of measurements containing only noise. The noises in these two channels share a common covariance matrix, up to a scale, which may be known or unknown. The signal model is a subspace model with variations: the subspace may be known or known only by its dimension; consecutive visits to the subspace may be unconstrained or they may be constrained by a prior distribution. As a consequence, there are four general classes of detectors and, within each class, there is a detector for the case where the scale between the primary and secondary channels is known, and for the case where this scale is unknown. The generalized likelihood ratio (GLR) based detectors derived in this paper, when organized with previously published GLR detectors, comprise a unified theory of adaptive subspace detection from primary and secondary channels of measurements.