Graph-signal Reconstruction and Blind Deconvolution for Structured Inputs
Paper and Code
Jun 01, 2021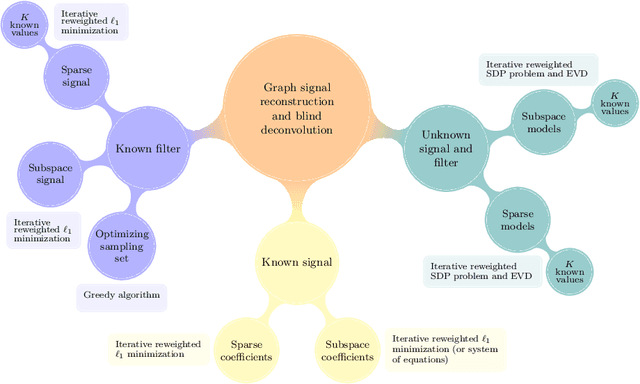
Key to successfully deal with complex contemporary datasets is the development of tractable models that account for the irregular structure of the information at hand. This paper provides a comprehensive and unifying view of several sampling, reconstruction, and recovery problems for signals defined on irregular domains that can be accurately represented by a graph. The workhorse assumption is that the (partially) observed signals can be modeled as the output of a graph filter to a structured (parsimonious) input graph signal. When either the input or the filter coefficients are known, this is tantamount to assuming that the signals of interest live on a subspace defined by the supporting graph. When neither is known, the model becomes bilinear. Upon imposing different priors and additional structure on either the input or the filter coefficients, a broad range of relevant problem formulations arise. The goal is then to leverage those priors, the shift operator of the supporting graph, and the samples of the signal of interest to recover: the signal at the non-sampled nodes (graph-signal interpolation), the input (deconvolution), the filter coefficients (system identification), or any combination thereof (blind deconvolution).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge