Efficient computational strategies to learn the structure of probabilistic graphical models of cumulative phenomena

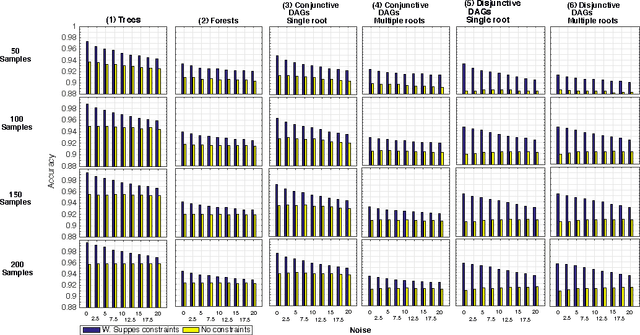
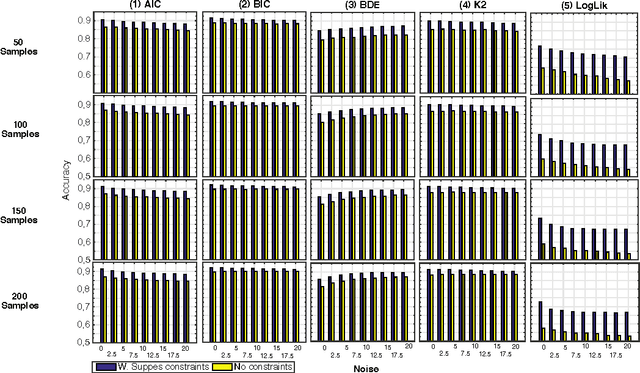
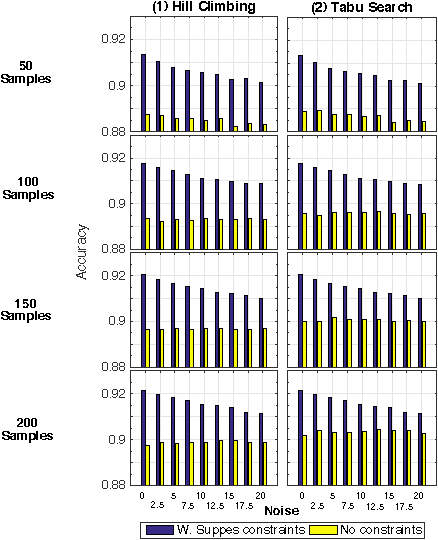
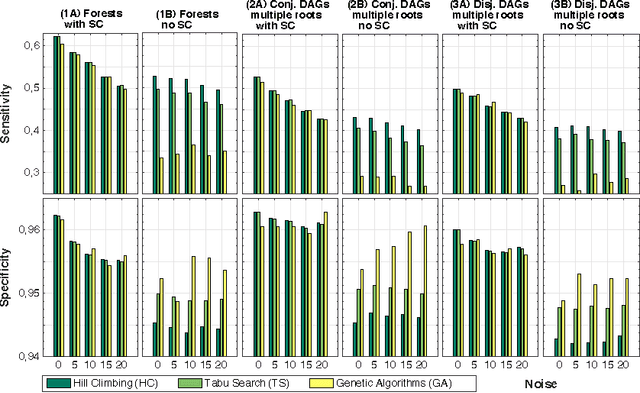
Structural learning of Bayesian Networks (BNs) is a NP-hard problem, which is further complicated by many theoretical issues, such as the I-equivalence among different structures. In this work, we focus on a specific subclass of BNs, named Suppes-Bayes Causal Networks (SBCNs), which include specific structural constraints based on Suppes' probabilistic causation to efficiently model cumulative phenomena. Here we compare the performance, via extensive simulations, of various state-of-the-art search strategies, such as local search techniques and Genetic Algorithms, as well as of distinct regularization methods. The assessment is performed on a large number of simulated datasets from topologies with distinct levels of complexity, various sample size and different rates of errors in the data. Among the main results, we show that the introduction of Suppes' constraints dramatically improve the inference accuracy, by reducing the solution space and providing a temporal ordering on the variables. We also report on trade-offs among different search techniques that can be efficiently employed in distinct experimental settings. This manuscript is an extended version of the paper "Structural Learning of Probabilistic Graphical Models of Cumulative Phenomena" presented at the 2018 International Conference on Computational Science.

Probabilistic Causal Analysis of Social Influence

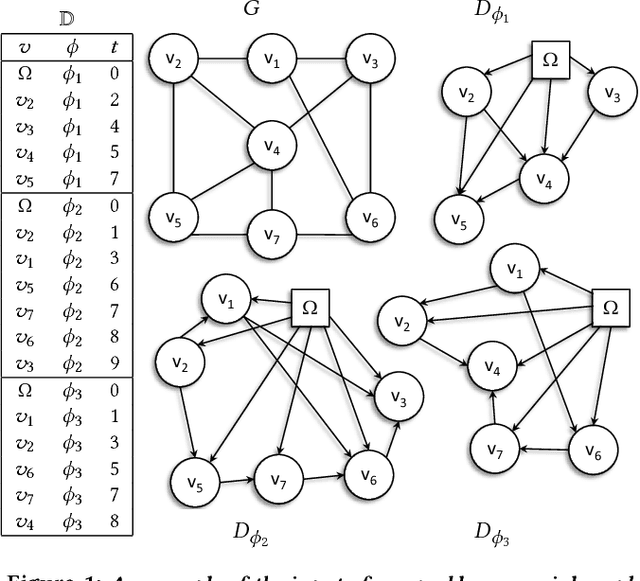
Mastering the dynamics of social influence requires separating, in a database of information propagation traces, the genuine causal processes from temporal correlation, i.e., homophily and other spurious causes. However, most studies to characterize social influence, and, in general, most data-science analyses focus on correlations, statistical independence, or conditional independence. Only recently, there has been a resurgence of interest in "causal data science", e.g., grounded on causality theories. In this paper we adopt a principled causal approach to the analysis of social influence from information-propagation data, rooted in the theory of probabilistic causation. Our approach consists of two phases. In the first one, in order to avoid the pitfalls of misinterpreting causation when the data spans a mixture of several subtypes ("Simpson's paradox"), we partition the set of propagation traces into groups, in such a way that each group is as less contradictory as possible in terms of the hierarchical structure of information propagation. To achieve this goal, we borrow the notion of "agony" and define the Agony-bounded Partitioning problem, which we prove being hard, and for which we develop two efficient algorithms with approximation guarantees. In the second phase, for each group from the first phase, we apply a constrained MLE approach to ultimately learn a minimal causal topology. Experiments on synthetic data show that our method is able to retrieve the genuine causal arcs w.r.t. a ground-truth generative model. Experiments on real data show that, by focusing only on the extracted causal structures instead of the whole social graph, the effectiveness of predicting influence spread is significantly improved.

Improved survival of cancer patients admitted to the ICU between 2002 and 2011 at a U.S. teaching hospital

Over the past decades, both critical care and cancer care have improved substantially. Due to increased cancer-specific survival, we hypothesized that both the number of cancer patients admitted to the ICU and overall survival have increased since the millennium change. MIMIC-III, a freely accessible critical care database of Beth Israel Deaconess Medical Center, Boston, USA was used to retrospectively study trends and outcomes of cancer patients admitted to the ICU between 2002 and 2011. Multiple logistic regression analysis was performed to adjust for confounders of 28-day and 1-year mortality. Out of 41,468 unique ICU admissions, 1,100 hemato-oncologic, 3,953 oncologic and 49 patients with both a hematological and solid malignancy were analyzed. Hematological patients had higher critical illness scores than non-cancer patients, while oncologic patients had similar APACHE-III and SOFA-scores compared to non-cancer patients. In the univariate analysis, cancer was strongly associated with mortality (OR= 2.74, 95%CI: 2.56, 2.94). Over the 10-year study period, 28-day mortality of cancer patients decreased by 30%. This trend persisted after adjustment for covariates, with cancer patients having significantly higher mortality (OR=2.63, 95%CI: 2.38, 2.88). Between 2002 and 2011, both the adjusted odds of 28-day mortality and the adjusted odds of 1-year mortality for cancer patients decreased by 6% (95%CI: 4%, 9%). Having cancer was the strongest single predictor of 1-year mortality in the multivariate model (OR=4.47, 95%CI: 4.11, 4.84).

Withholding aggressive treatments may not accelerate time to death among dying ICU patients

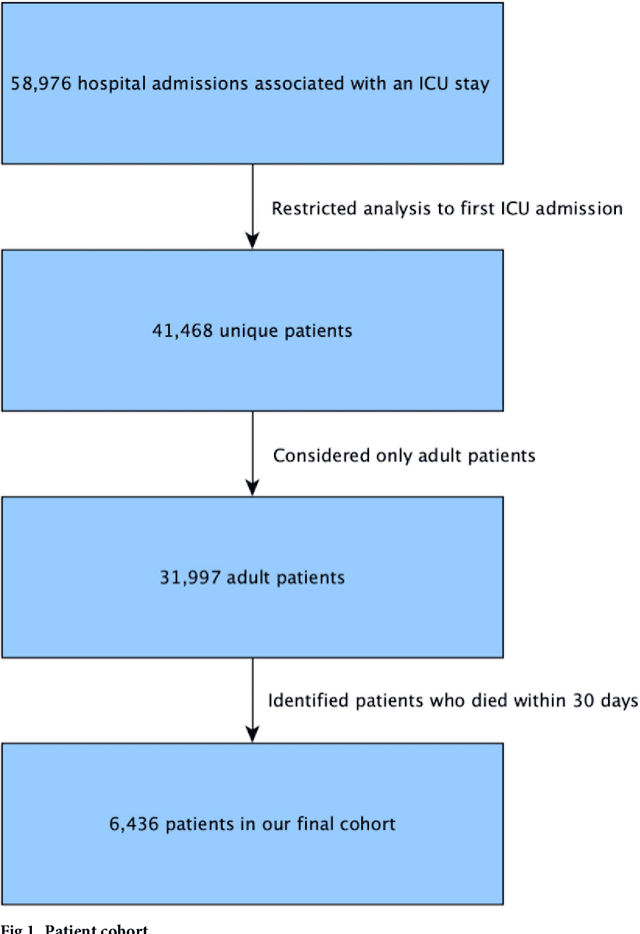
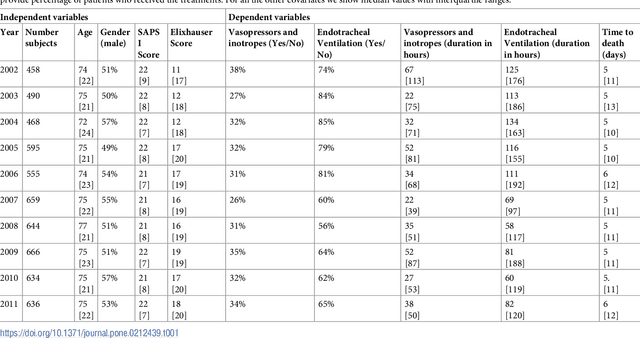
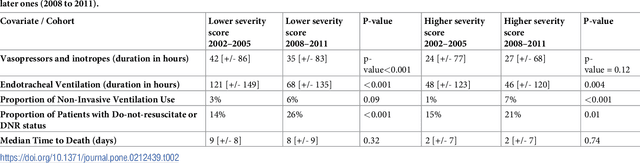
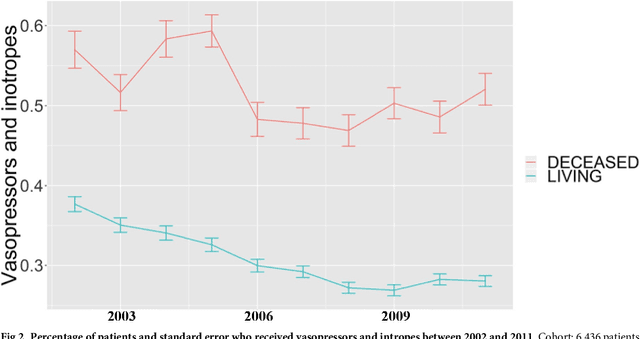
Critically ill patients may die despite aggressive treatment. In this study, we examine trends in the application of two such treatments over a decade, as well as the impact of these trends on survival durations in patients who die within a month of ICU admission. We considered observational data available from the MIMIC-III open-access ICU database, collected from June 2001 to October 2012: These data comprise almost 60,000 hospital admissions for a total of 38,645 unique adults. We explored two hypotheses: (i) administration of aggressive treatment during the ICU stay immediately preceding end-of-life would decrease over the study time period and (ii) time-to-death from ICU admission would also decrease due to the decrease in aggressive treatment administration. Tests for significant trends were performed and a p-value threshold of 0.05 was used to assess statistical significance. We found that aggressive treatments in this population were employed with decreasing frequency over the study period duration, and also that reducing aggressive treatments for such patients may not result in shorter times to death. The latter finding has implications for end of life discussions that involve the possible use or non-use of such treatments in those patients with very poor prognosis.

Multi-objective optimization to explicitly account for model complexity when learning Bayesian Networks

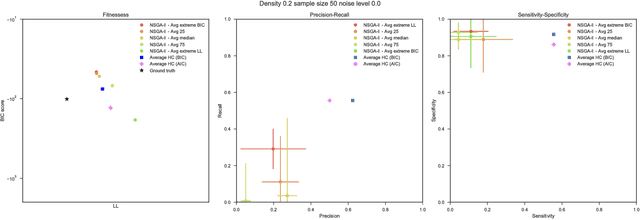
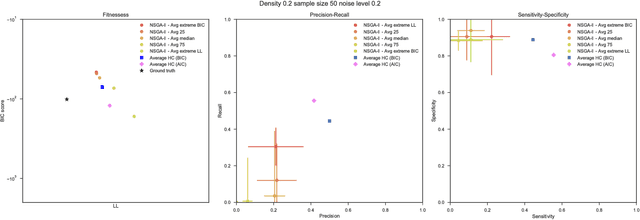
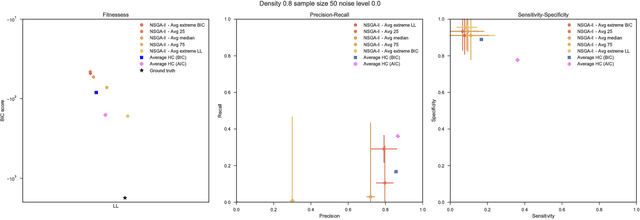
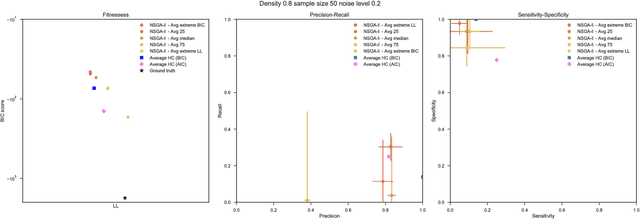
Bayesian Networks have been widely used in the last decades in many fields, to describe statistical dependencies among random variables. In general, learning the structure of such models is a problem with considerable theoretical interest that still poses many challenges. On the one hand, this is a well-known NP-complete problem, which is practically hardened by the huge search space of possible solutions. On the other hand, the phenomenon of I-equivalence, i.e., different graphical structures underpinning the same set of statistical dependencies, may lead to multimodal fitness landscapes further hindering maximum likelihood approaches to solve the task. Despite all these difficulties, greedy search methods based on a likelihood score coupled with a regularization term to account for model complexity, have been shown to be surprisingly effective in practice. In this paper, we consider the formulation of the task of learning the structure of Bayesian Networks as an optimization problem based on a likelihood score. Nevertheless, our approach do not adjust this score by means of any of the complexity terms proposed in the literature; instead, it accounts directly for the complexity of the discovered solutions by exploiting a multi-objective optimization procedure. To this extent, we adopt NSGA-II and define the first objective function to be the likelihood of a solution and the second to be the number of selected arcs. We thoroughly analyze the behavior of our method on a wide set of simulated data, and we discuss the performance considering the goodness of the inferred solutions both in terms of their objective functions and with respect to the retrieved structure. Our results show that NSGA-II can converge to solutions characterized by better likelihood and less arcs than classic approaches, although paradoxically frequently characterized by a lower similarity to the target network.

Learning the structure of Bayesian Networks: A quantitative assessment of the effect of different algorithmic schemes

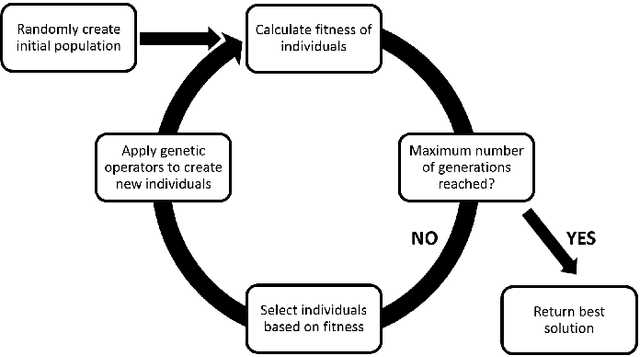
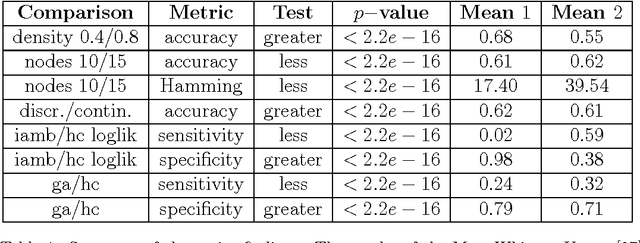
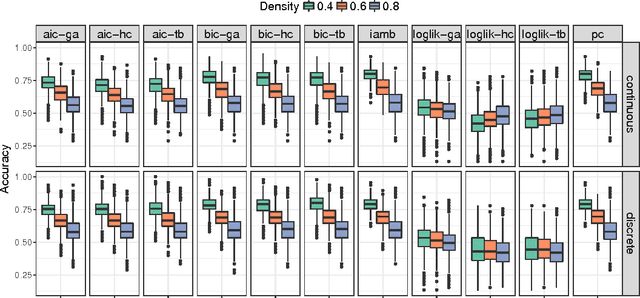
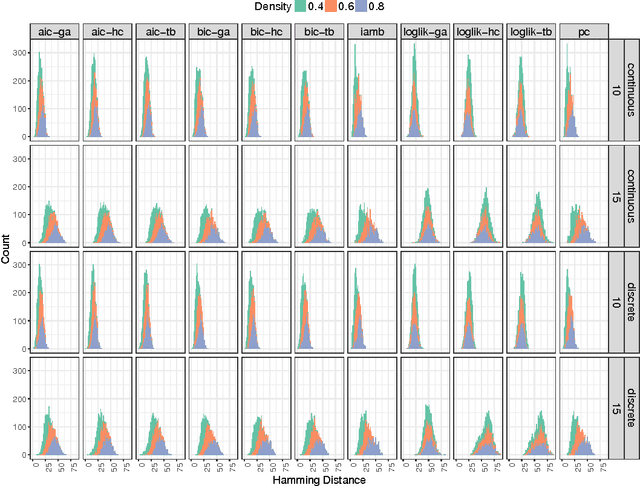
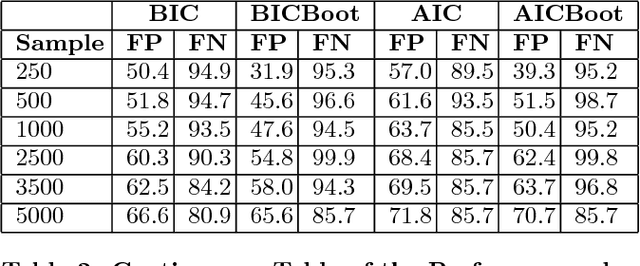
One of the most challenging tasks when adopting Bayesian Networks (BNs) is the one of learning their structure from data. This task is complicated by the huge search space of possible solutions, and by the fact that the problem is NP-hard. Hence, full enumeration of all the possible solutions is not always feasible and approximations are often required. However, to the best of our knowledge, a quantitative analysis of the performance and characteristics of the different heuristics to solve this problem has never been done before. For this reason, in this work, we provide a detailed comparison of many different state-of-the-arts methods for structural learning on simulated data considering both BNs with discrete and continuous variables, and with different rates of noise in the data. In particular, we investigate the performance of different widespread scores and algorithmic approaches proposed for the inference and the statistical pitfalls within them.

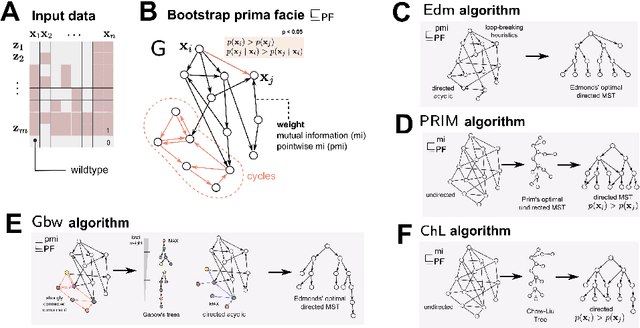
Modeling cumulative biological phenomena with Suppes-Bayes Causal Networks

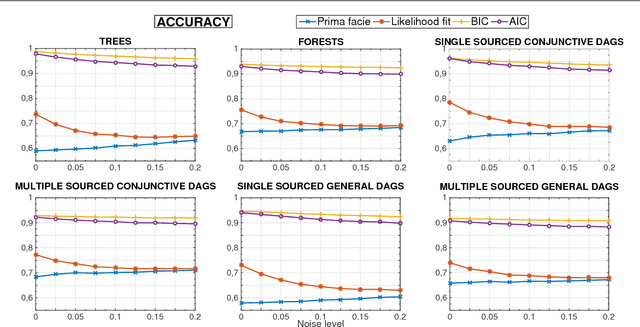
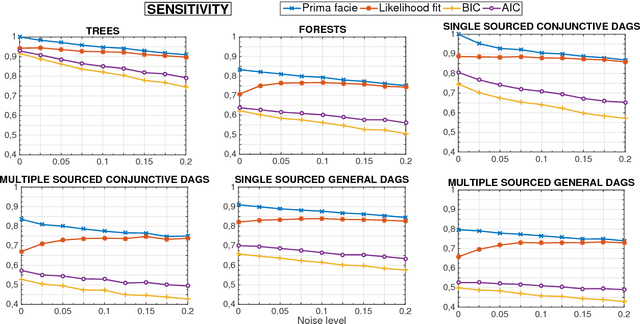
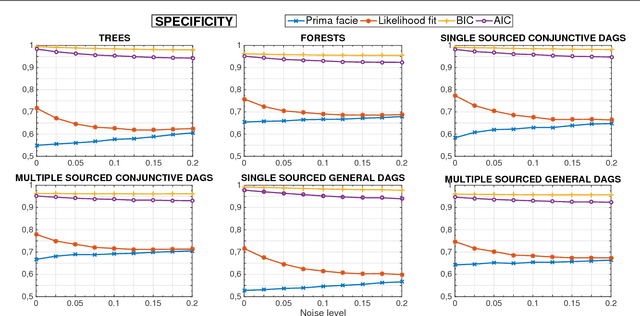
Several diseases related to cell proliferation are characterized by the accumulation of somatic DNA changes, with respect to wildtype conditions. Cancer and HIV are two common examples of such diseases, where the mutational load in the cancerous/viral population increases over time. In these cases, selective pressures are often observed along with competition, cooperation and parasitism among distinct cellular clones. Recently, we presented a mathematical framework to model these phenomena, based on a combination of Bayesian inference and Suppes' theory of probabilistic causation, depicted in graphical structures dubbed Suppes-Bayes Causal Networks (SBCNs). SBCNs are generative probabilistic graphical models that recapitulate the potential ordering of accumulation of such DNA changes during the progression of the disease. Such models can be inferred from data by exploiting likelihood-based model-selection strategies with regularization. In this paper we discuss the theoretical foundations of our approach and we investigate in depth the influence on the model-selection task of: (i) the poset based on Suppes' theory and (ii) different regularization strategies. Furthermore, we provide an example of application of our framework to HIV genetic data highlighting the valuable insights provided by the inferred.

Causal Data Science for Financial Stress Testing

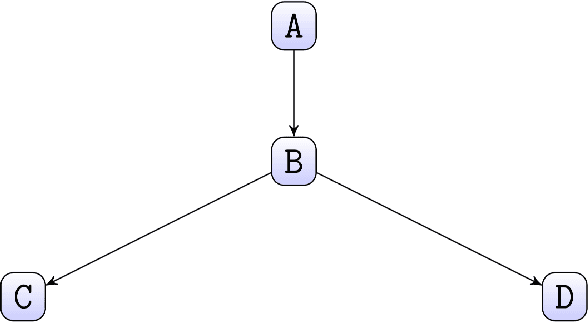
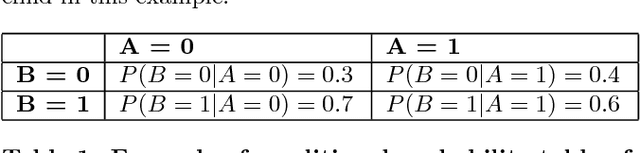
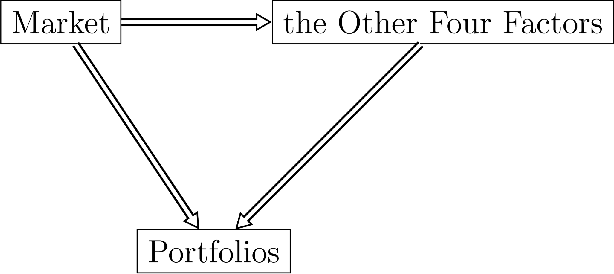
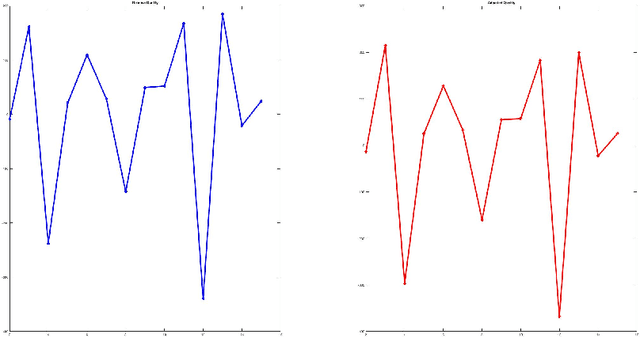
The most recent financial upheavals have cast doubt on the adequacy of some of the conventional quantitative risk management strategies, such as VaR (Value at Risk), in many common situations. Consequently, there has been an increasing need for verisimilar financial stress testings, namely simulating and analyzing financial portfolios in extreme, albeit rare scenarios. Unlike conventional risk management which exploits statistical correlations among financial instruments, here we focus our analysis on the notion of probabilistic causation, which is embodied by Suppes-Bayes Causal Networks (SBCNs); SBCNs are probabilistic graphical models that have many attractive features in terms of more accurate causal analysis for generating financial stress scenarios. In this paper, we present a novel approach for conducting stress testing of financial portfolios based on SBCNs in combination with classical machine learning classification tools. The resulting method is shown to be capable of correctly discovering the causal relationships among financial factors that affect the portfolios and thus, simulating stress testing scenarios with a higher accuracy and lower computational complexity than conventional Monte Carlo Simulations.

SIMLR: A Tool for Large-Scale Genomic Analyses by Multi-Kernel Learning

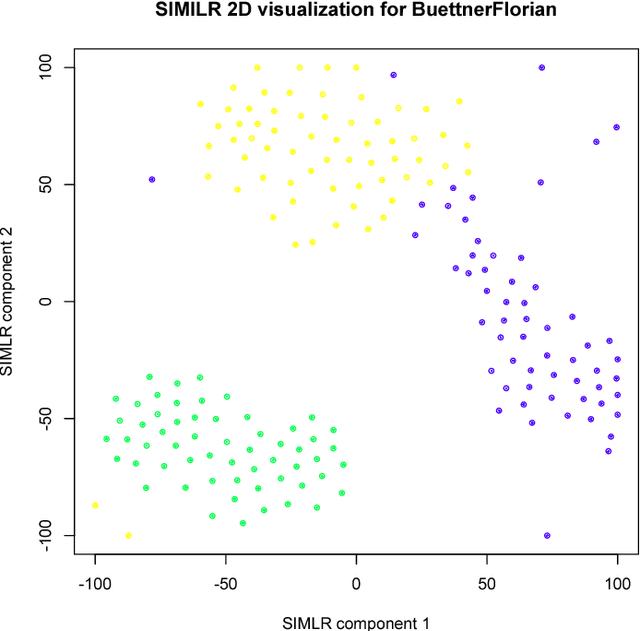
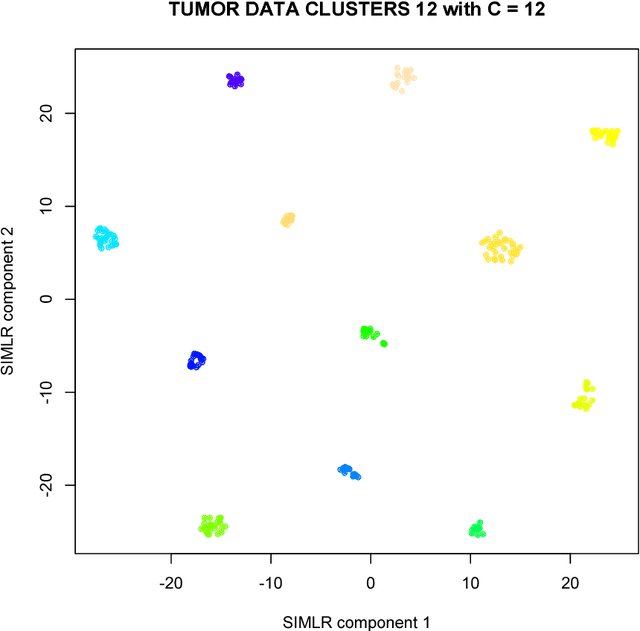
We here present SIMLR (Single-cell Interpretation via Multi-kernel LeaRning), an open-source tool that implements a novel framework to learn a sample-to-sample similarity measure from expression data observed for heterogenous samples. SIMLR can be effectively used to perform tasks such as dimension reduction, clustering, and visualization of heterogeneous populations of samples. SIMLR was benchmarked against state-of-the-art methods for these three tasks on several public datasets, showing it to be scalable and capable of greatly improving clustering performance, as well as providing valuable insights by making the data more interpretable via better a visualization. Availability and Implementation SIMLR is available on GitHub in both R and MATLAB implementations. Furthermore, it is also available as an R package on http://bioconductor.org.

Learning mutational graphs of individual tumor evolution from multi-sample sequencing data

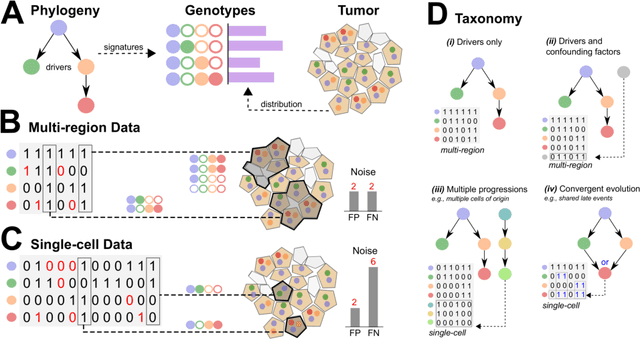
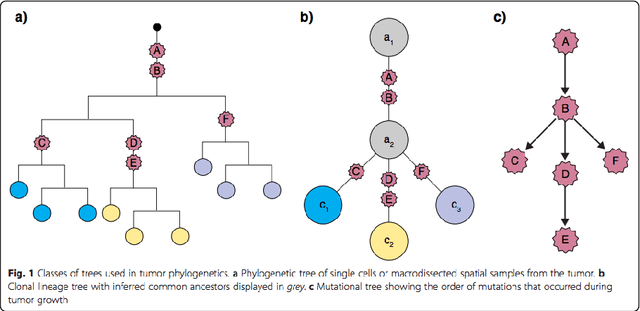
Phylogenetic techniques quantify intra-tumor heterogeneity by deconvolving either clonal or mutational trees from multi-sample sequencing data of individual tumors. Most of these methods rely on the well-known infinite sites assumption, and are limited to process either multi-region or single-cell sequencing data. Here, we improve over those methods with TRaIT, a unified statistical framework for the inference of the accumula- tion order of multiple types of genomic alterations driving tumor development. TRaIT supports both multi-region and single-cell sequencing data, and output mutational graphs accounting for violations of the infinite sites assumption due to convergent evolution, and other complex phenomena that cannot be detected with phylogenetic tools. Our method displays better accuracy, performance and robustness to noise and small sample size than state-of-the-art phylogenetic methods. We show with single-cell data from breast cancer and multi-region data from colorectal cancer that TRaIT can quantify the extent of intra-tumor heterogeneity and generate new testable experimental hypotheses.