Modeling Epidemiological Dynamics Under Adversarial Data and User Deception

Epidemiological models increasingly rely on self-reported behavioral data such as vaccination status, mask usage, and social distancing adherence to forecast disease transmission and assess the impact of non-pharmaceutical interventions (NPIs). While such data provide valuable real-time insights, they are often subject to strategic misreporting, driven by individual incentives to avoid penalties, access benefits, or express distrust in public health authorities. To account for such human behavior, in this paper, we introduce a game-theoretic framework that models the interaction between the population and a public health authority as a signaling game. Individuals (senders) choose how to report their behaviors, while the public health authority (receiver) updates their epidemiological model(s) based on potentially distorted signals. Focusing on deception around masking and vaccination, we characterize analytically game equilibrium outcomes and evaluate the degree to which deception can be tolerated while maintaining epidemic control through policy interventions. Our results show that separating equilibria-with minimal deception-drive infections to near zero over time. Remarkably, even under pervasive dishonesty in pooling equilibria, well-designed sender and receiver strategies can still maintain effective epidemic control. This work advances the understanding of adversarial data in epidemiology and offers tools for designing more robust public health models in the presence of strategic user behavior.

Efficient Evolutionary Models with Digraphons

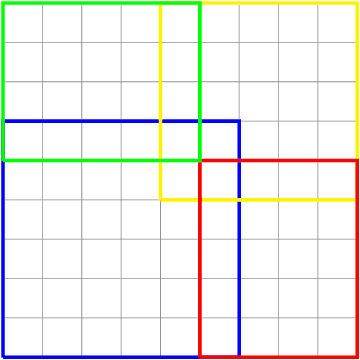
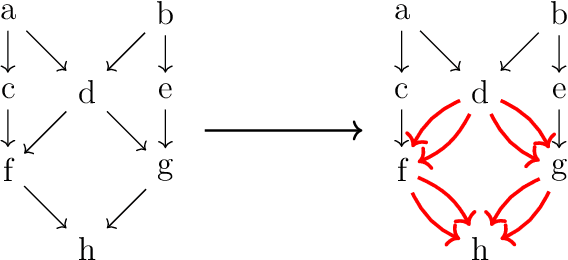
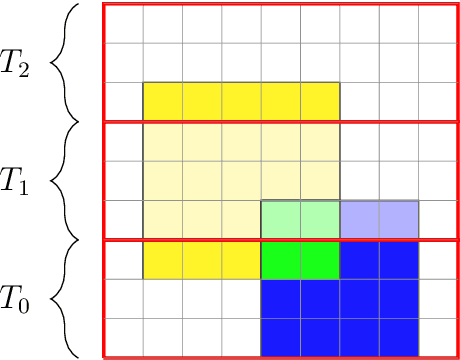
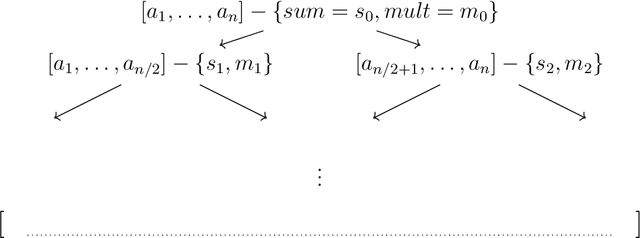
We present two main contributions which help us in leveraging the theory of graphons for modeling evolutionary processes. We show a generative model for digraphons using a finite basis of subgraphs, which is representative of biological networks with evolution by duplication. We show a simple MAP estimate on the Bayesian non parametric model using the Dirichlet Chinese restaurant process representation, with the help of a Gibbs sampling algorithm to infer the prior. Next we show an efficient implementation to do simulations on finite basis segmentations of digraphons. This implementation is used for developing fast evolutionary simulations with the help of an efficient 2-D representation of the digraphon using dynamic segment-trees with the square-root decomposition representation. We further show how this representation is flexible enough to handle changing graph nodes and can be used to also model dynamic digraphons with the help of an amortized update representation to achieve an efficient time complexity of the update at $O(\sqrt{|V|}\log{|V|})$.

To mock a Mocking bird : Studies in Biomimicry

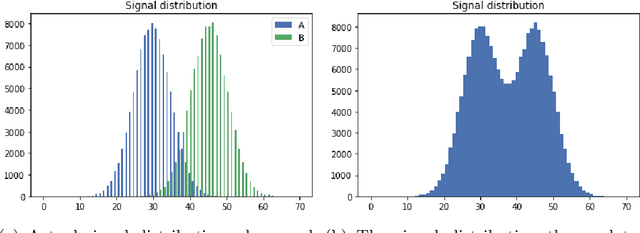
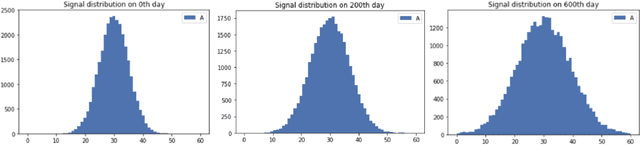
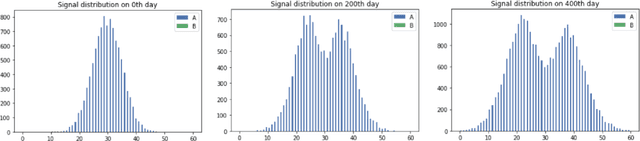
This paper dwells on certain novel game-theoretic investigations in bio-mimicry, discussed from the perspectives of information asymmetry, individual utility and its optimization via strategic interactions involving co-evolving preys (e.g., insects) and predators (e.g., reptiles) who learn. Formally, we consider a panmictic ecosystem, occupied by species of prey with relatively short lifespan, which evolve mimicry signals over generations as they interact with predators with relatively longer lifespans, thus endowing predators with the ability to learn prey signals. Every prey sends a signal and provides utility to the predator. The prey can be either nutritious or toxic to the predator, but the prey may signal (possibly) deceptively without revealing its true "type." The model is used to study the situation where multi-armed bandit predators with zero prior information are introduced into the ecosystem. As a result of exploration and exploitation the predators naturally select the prey that result in the evolution of those signals. This co-evolution of strategies produces a variety of interesting phenomena which are subjects of this paper.

Creolizing the Web

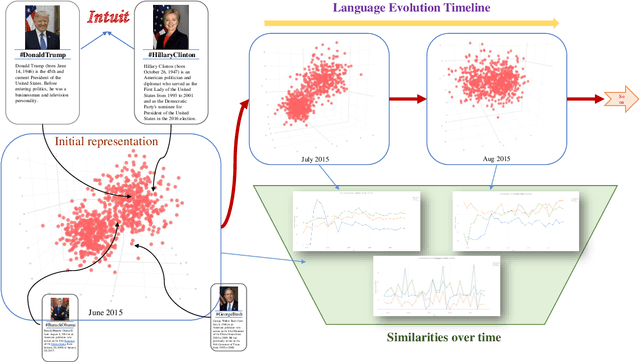
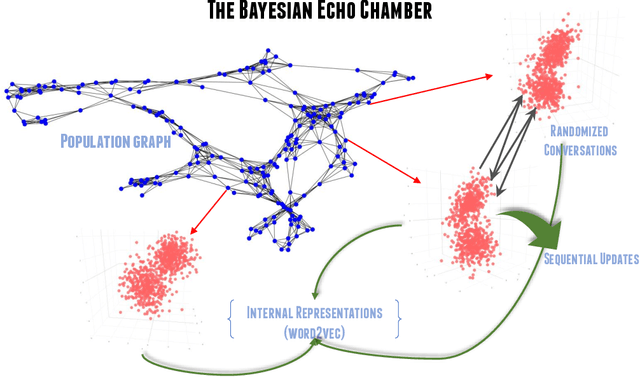
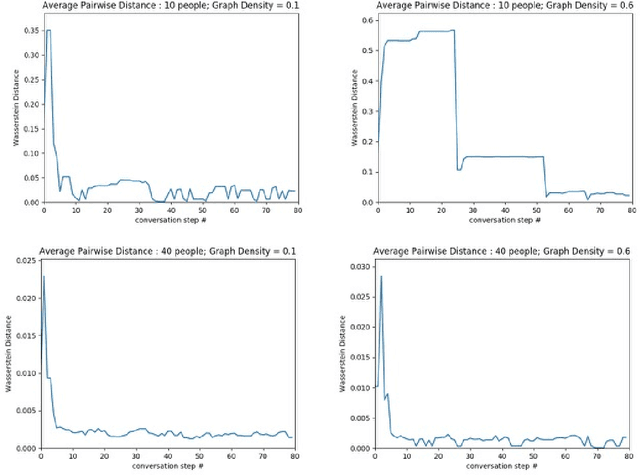
The evolution of language has been a hotly debated subject with contradicting hypotheses and unreliable claims. Drawing from signalling games, dynamic population mechanics, machine learning and algebraic topology, we present a method for detecting evolutionary patterns in a sociological model of language evolution. We develop a minimalistic model that provides a rigorous base for any generalized evolutionary model for language based on communication between individuals. We also discuss theoretical guarantees of this model, ranging from stability of language representations to fast convergence of language by temporal communication and language drift in an interactive setting. Further we present empirical results and their interpretations on a real world dataset from \rdt to identify communities and echo chambers for opinions, thus placing obstructions to reliable communication among communities.

Decidability in Robot Manipulation Planning

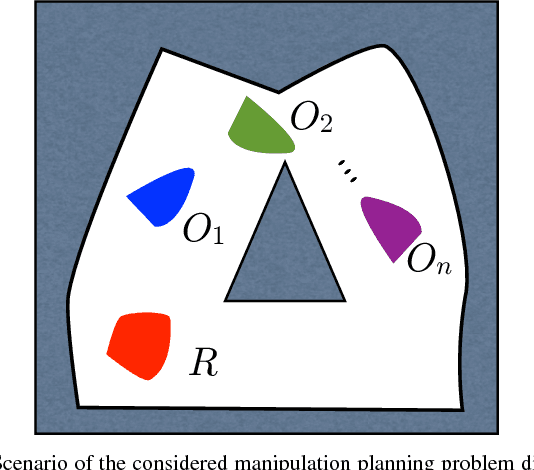
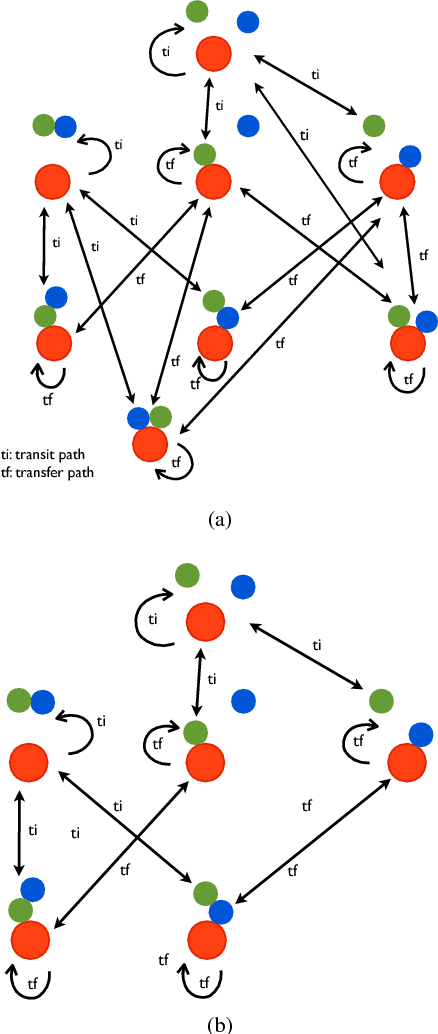
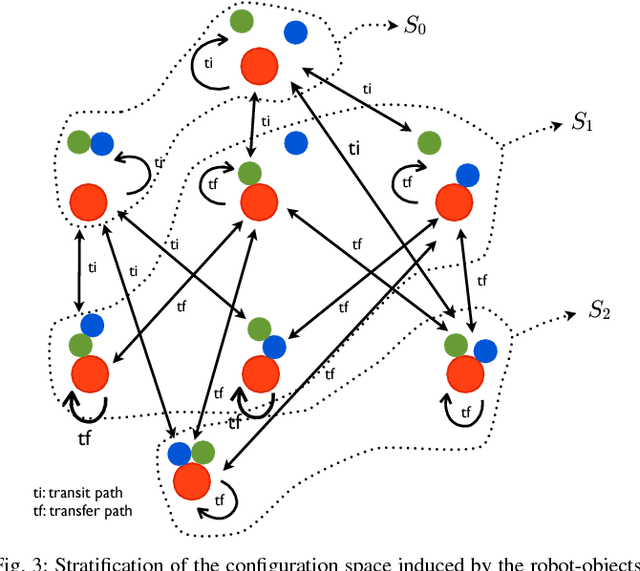
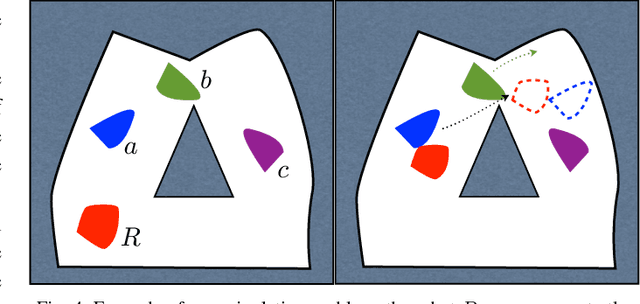
Consider the problem of planning collision-free motion of $n$ objects in the plane movable through contact with a robot that can autonomously translate in the plane and that can move a maximum of $m \leq n$ objects simultaneously. This represents the abstract formulation of a manipulation planning problem that is proven to be decidable in this paper. The tools used for proving decidability of this simplified manipulation planning problem are, in fact, general enough to handle the decidability problem for the wider class of systems characterized by a stratified configuration space. These include, for example, problems of legged and multi-contact locomotion, bi-manual manipulation. In addition, the described approach does not restrict the dynamics of the manipulation system to be considered.

Probabilistic Causal Analysis of Social Influence

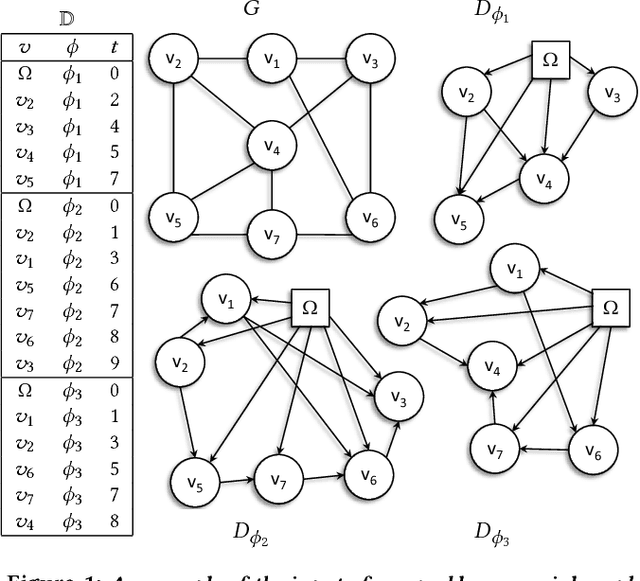
Mastering the dynamics of social influence requires separating, in a database of information propagation traces, the genuine causal processes from temporal correlation, i.e., homophily and other spurious causes. However, most studies to characterize social influence, and, in general, most data-science analyses focus on correlations, statistical independence, or conditional independence. Only recently, there has been a resurgence of interest in "causal data science", e.g., grounded on causality theories. In this paper we adopt a principled causal approach to the analysis of social influence from information-propagation data, rooted in the theory of probabilistic causation. Our approach consists of two phases. In the first one, in order to avoid the pitfalls of misinterpreting causation when the data spans a mixture of several subtypes ("Simpson's paradox"), we partition the set of propagation traces into groups, in such a way that each group is as less contradictory as possible in terms of the hierarchical structure of information propagation. To achieve this goal, we borrow the notion of "agony" and define the Agony-bounded Partitioning problem, which we prove being hard, and for which we develop two efficient algorithms with approximation guarantees. In the second phase, for each group from the first phase, we apply a constrained MLE approach to ultimately learn a minimal causal topology. Experiments on synthetic data show that our method is able to retrieve the genuine causal arcs w.r.t. a ground-truth generative model. Experiments on real data show that, by focusing only on the extracted causal structures instead of the whole social graph, the effectiveness of predicting influence spread is significantly improved.

Causal Data Science for Financial Stress Testing

The most recent financial upheavals have cast doubt on the adequacy of some of the conventional quantitative risk management strategies, such as VaR (Value at Risk), in many common situations. Consequently, there has been an increasing need for verisimilar financial stress testings, namely simulating and analyzing financial portfolios in extreme, albeit rare scenarios. Unlike conventional risk management which exploits statistical correlations among financial instruments, here we focus our analysis on the notion of probabilistic causation, which is embodied by Suppes-Bayes Causal Networks (SBCNs); SBCNs are probabilistic graphical models that have many attractive features in terms of more accurate causal analysis for generating financial stress scenarios. In this paper, we present a novel approach for conducting stress testing of financial portfolios based on SBCNs in combination with classical machine learning classification tools. The resulting method is shown to be capable of correctly discovering the causal relationships among financial factors that affect the portfolios and thus, simulating stress testing scenarios with a higher accuracy and lower computational complexity than conventional Monte Carlo Simulations.

Exposing the Probabilistic Causal Structure of Discrimination

Discrimination discovery from data is an important task aiming at identifying patterns of illegal and unethical discriminatory activities against protected-by-law groups, e.g., ethnic minorities. While any legally-valid proof of discrimination requires evidence of causality, the state-of-the-art methods are essentially correlation-based, albeit, as it is well known, correlation does not imply causation. In this paper we take a principled causal approach to the data mining problem of discrimination detection in databases. Following Suppes' probabilistic causation theory, we define a method to extract, from a dataset of historical decision records, the causal structures existing among the attributes in the data. The result is a type of constrained Bayesian network, which we dub Suppes-Bayes Causal Network (SBCN). Next, we develop a toolkit of methods based on random walks on top of the SBCN, addressing different anti-discrimination legal concepts, such as direct and indirect discrimination, group and individual discrimination, genuine requirement, and favoritism. Our experiments on real-world datasets confirm the inferential power of our approach in all these different tasks.

Inference of Cancer Progression Models with Biological Noise

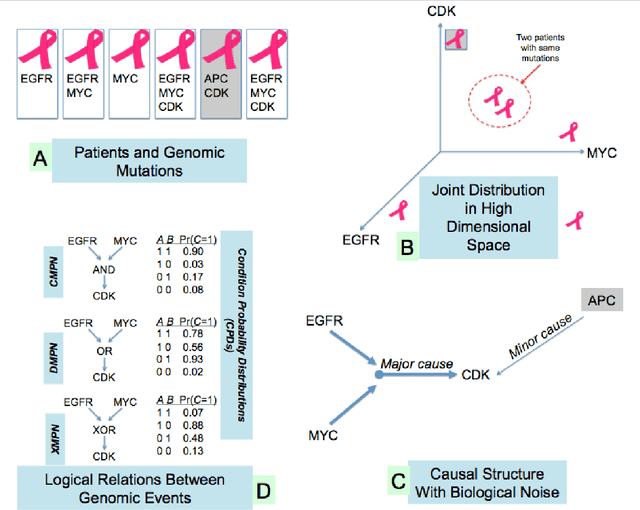
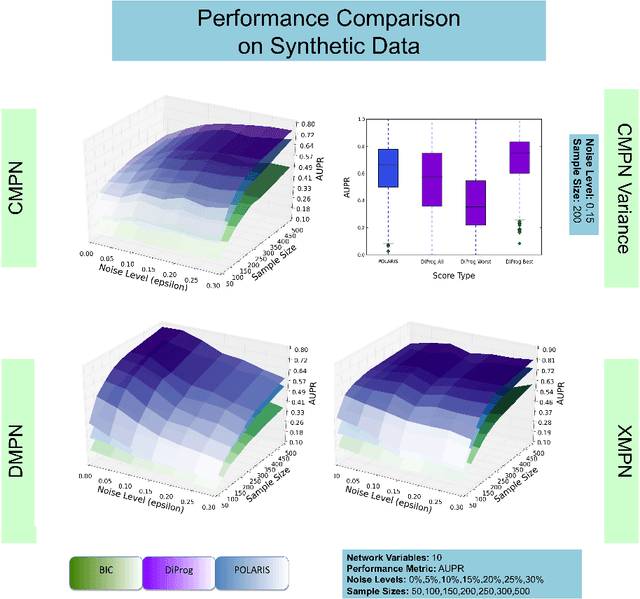
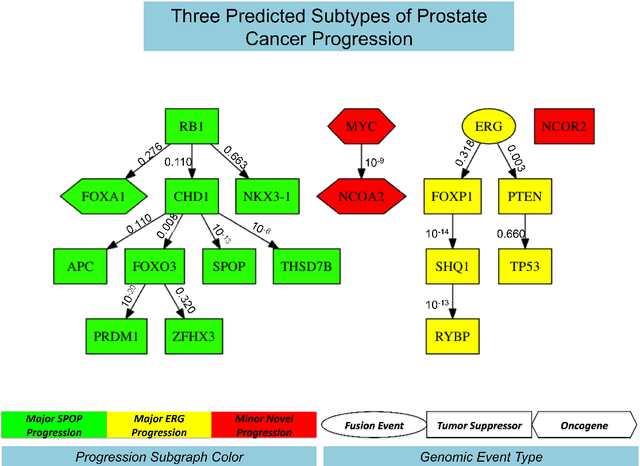
Many applications in translational medicine require the understanding of how diseases progress through the accumulation of persistent events. Specialized Bayesian networks called monotonic progression networks offer a statistical framework for modeling this sort of phenomenon. Current machine learning tools to reconstruct Bayesian networks from data are powerful but not suited to progression models. We combine the technological advances in machine learning with a rigorous philosophical theory of causation to produce Polaris, a scalable algorithm for learning progression networks that accounts for causal or biological noise as well as logical relations among genetic events, making the resulting models easy to interpret qualitatively. We tested Polaris on synthetically generated data and showed that it outperforms a widely used machine learning algorithm and approaches the performance of the competing special-purpose, albeit clairvoyant algorithm that is given a priori information about the model parameters. We also prove that under certain rather mild conditions, Polaris is guaranteed to converge for sufficiently large sample sizes. Finally, we applied Polaris to point mutation and copy number variation data in Prostate cancer from The Cancer Genome Atlas (TCGA) and found that there are likely three distinct progressions, one major androgen driven progression, one major non-androgen driven progression, and one novel minor androgen driven progression.

The Temporal Logic of Causal Structures

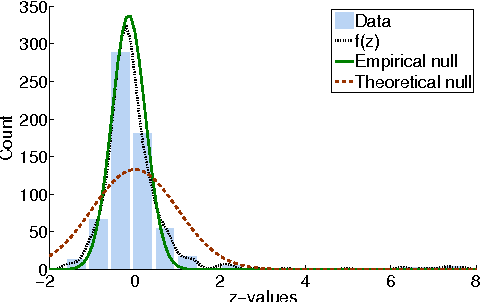
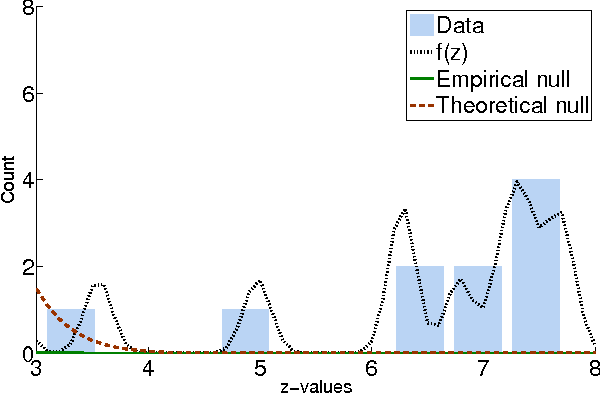
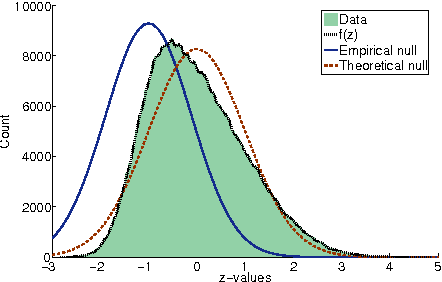
Computational analysis of time-course data with an underlying causal structure is needed in a variety of domains, including neural spike trains, stock price movements, and gene expression levels. However, it can be challenging to determine from just the numerical time course data alone what is coordinating the visible processes, to separate the underlying prima facie causes into genuine and spurious causes and to do so with a feasible computational complexity. For this purpose, we have been developing a novel algorithm based on a framework that combines notions of causality in philosophy with algorithmic approaches built on model checking and statistical techniques for multiple hypotheses testing. The causal relationships are described in terms of temporal logic formulae, reframing the inference problem in terms of model checking. The logic used, PCTL, allows description of both the time between cause and effect and the probability of this relationship being observed. We show that equipped with these causal formulae with their associated probabilities we may compute the average impact a cause makes to its effect and then discover statistically significant causes through the concepts of multiple hypothesis testing (treating each causal relationship as a hypothesis), and false discovery control. By exploring a well-chosen family of potentially all significant hypotheses with reasonably minimal description length, it is possible to tame the algorithm's computational complexity while exploring the nearly complete search-space of all prima facie causes. We have tested these ideas in a number of domains and illustrate them here with two examples.