Francesco Gullo
Probabilistic Causal Analysis of Social Influence
Aug 29, 2018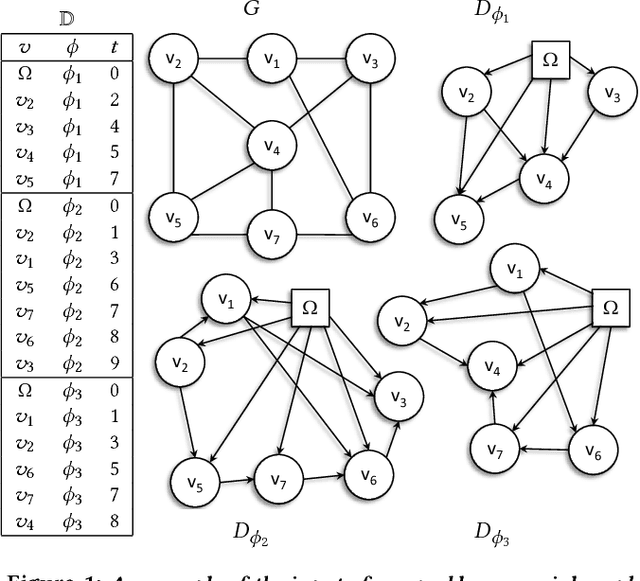
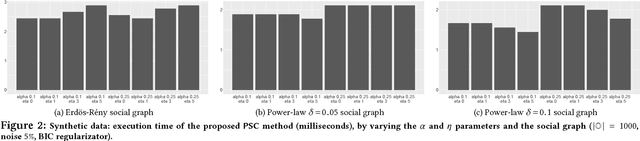
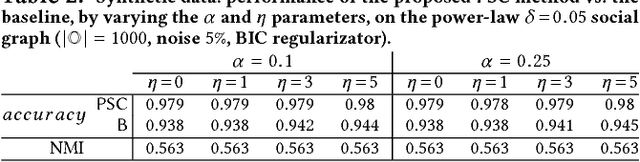

Abstract:Mastering the dynamics of social influence requires separating, in a database of information propagation traces, the genuine causal processes from temporal correlation, i.e., homophily and other spurious causes. However, most studies to characterize social influence, and, in general, most data-science analyses focus on correlations, statistical independence, or conditional independence. Only recently, there has been a resurgence of interest in "causal data science", e.g., grounded on causality theories. In this paper we adopt a principled causal approach to the analysis of social influence from information-propagation data, rooted in the theory of probabilistic causation. Our approach consists of two phases. In the first one, in order to avoid the pitfalls of misinterpreting causation when the data spans a mixture of several subtypes ("Simpson's paradox"), we partition the set of propagation traces into groups, in such a way that each group is as less contradictory as possible in terms of the hierarchical structure of information propagation. To achieve this goal, we borrow the notion of "agony" and define the Agony-bounded Partitioning problem, which we prove being hard, and for which we develop two efficient algorithms with approximation guarantees. In the second phase, for each group from the first phase, we apply a constrained MLE approach to ultimately learn a minimal causal topology. Experiments on synthetic data show that our method is able to retrieve the genuine causal arcs w.r.t. a ground-truth generative model. Experiments on real data show that, by focusing only on the extracted causal structures instead of the whole social graph, the effectiveness of predicting influence spread is significantly improved.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge