Abhinav Tamaskar
Efficient Evolutionary Models with Digraphons
Apr 26, 2021
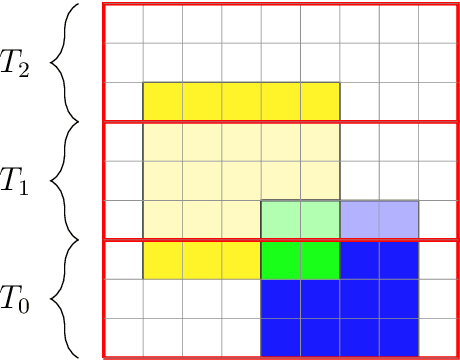
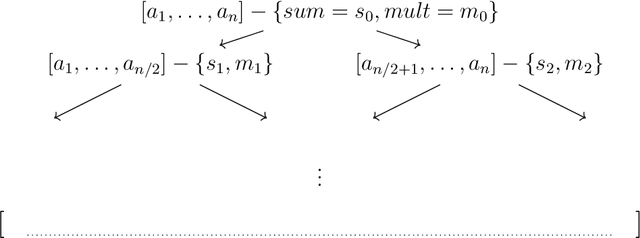
Abstract:We present two main contributions which help us in leveraging the theory of graphons for modeling evolutionary processes. We show a generative model for digraphons using a finite basis of subgraphs, which is representative of biological networks with evolution by duplication. We show a simple MAP estimate on the Bayesian non parametric model using the Dirichlet Chinese restaurant process representation, with the help of a Gibbs sampling algorithm to infer the prior. Next we show an efficient implementation to do simulations on finite basis segmentations of digraphons. This implementation is used for developing fast evolutionary simulations with the help of an efficient 2-D representation of the digraphon using dynamic segment-trees with the square-root decomposition representation. We further show how this representation is flexible enough to handle changing graph nodes and can be used to also model dynamic digraphons with the help of an amortized update representation to achieve an efficient time complexity of the update at $O(\sqrt{|V|}\log{|V|})$.
Creolizing the Web
Feb 24, 2021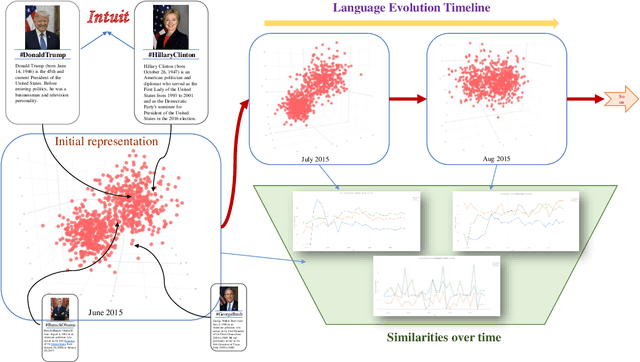

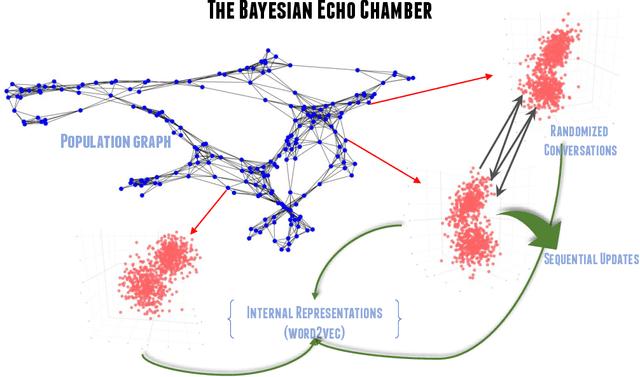
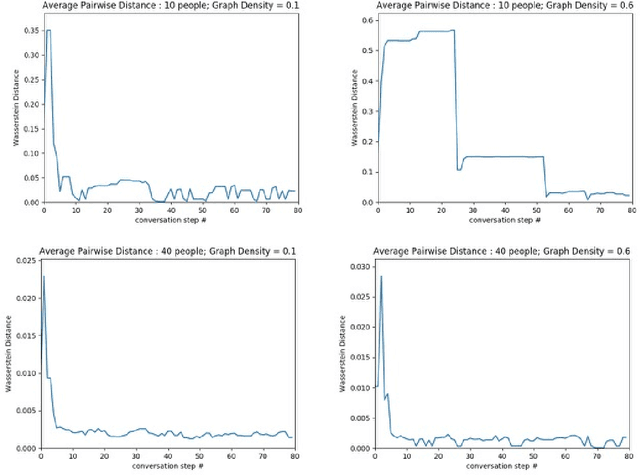
Abstract:The evolution of language has been a hotly debated subject with contradicting hypotheses and unreliable claims. Drawing from signalling games, dynamic population mechanics, machine learning and algebraic topology, we present a method for detecting evolutionary patterns in a sociological model of language evolution. We develop a minimalistic model that provides a rigorous base for any generalized evolutionary model for language based on communication between individuals. We also discuss theoretical guarantees of this model, ranging from stability of language representations to fast convergence of language by temporal communication and language drift in an interactive setting. Further we present empirical results and their interpretations on a real world dataset from \rdt to identify communities and echo chambers for opinions, thus placing obstructions to reliable communication among communities.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge