USE-Net: incorporating Squeeze-and-Excitation blocks into U-Net for prostate zonal segmentation of multi-institutional MRI datasets

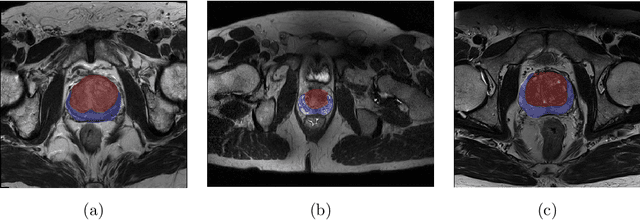
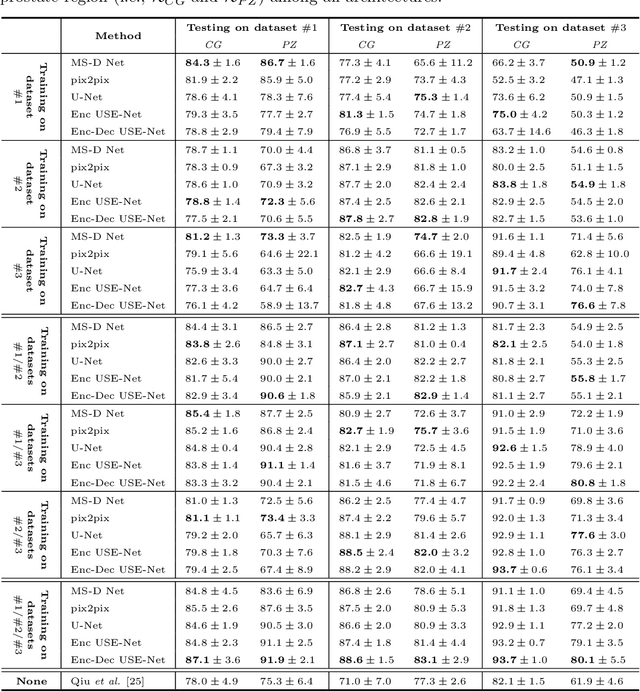
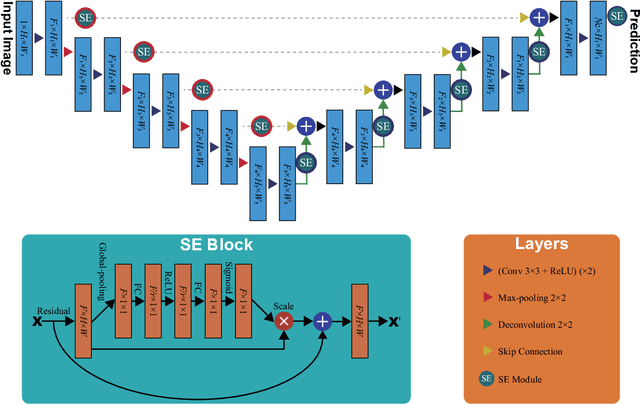
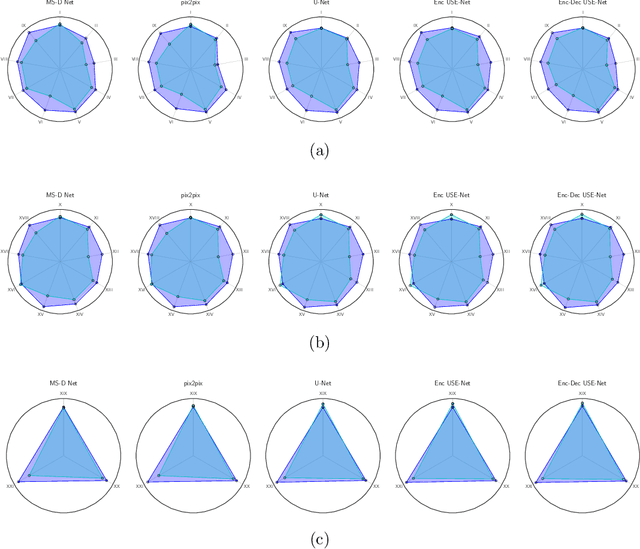
Prostate cancer is the most common malignant tumors in men but prostate Magnetic Resonance Imaging (MRI) analysis remains challenging. Besides whole prostate gland segmentation, the capability to differentiate between the blurry boundary of the Central Gland (CG) and Peripheral Zone (PZ) can lead to differential diagnosis, since tumor's frequency and severity differ in these regions. To tackle the prostate zonal segmentation task, we propose a novel Convolutional Neural Network (CNN), called USE-Net, which incorporates Squeeze-and-Excitation (SE) blocks into U-Net. Especially, the SE blocks are added after every Encoder (Enc USE-Net) or Encoder-Decoder block (Enc-Dec USE-Net). This study evaluates the generalization ability of CNN-based architectures on three T2-weighted MRI datasets, each one consisting of a different number of patients and heterogeneous image characteristics, collected by different institutions. The following mixed scheme is used for training/testing: (i) training on either each individual dataset or multiple prostate MRI datasets and (ii) testing on all three datasets with all possible training/testing combinations. USE-Net is compared against three state-of-the-art CNN-based architectures (i.e., U-Net, pix2pix, and Mixed-Scale Dense Network), along with a semi-automatic continuous max-flow model. The results show that training on the union of the datasets generally outperforms training on each dataset separately, allowing for both intra-/cross-dataset generalization. Enc USE-Net shows good overall generalization under any training condition, while Enc-Dec USE-Net remarkably outperforms the other methods when trained on all datasets. These findings reveal that the SE blocks' adaptive feature recalibration provides excellent cross-dataset generalization when testing is performed on samples of the datasets used during training.

Multi-objective optimization to explicitly account for model complexity when learning Bayesian Networks

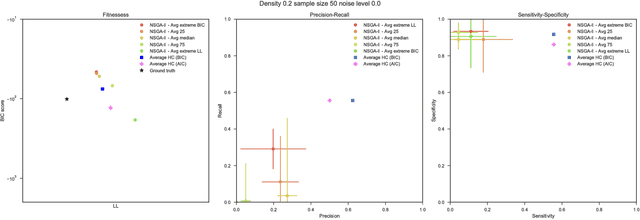
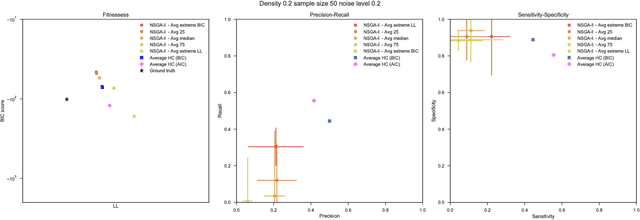
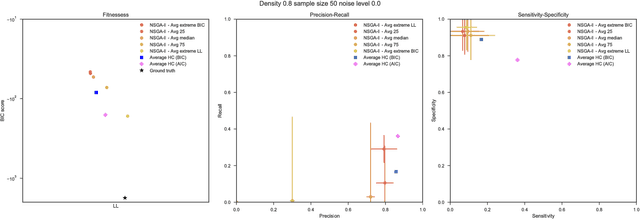
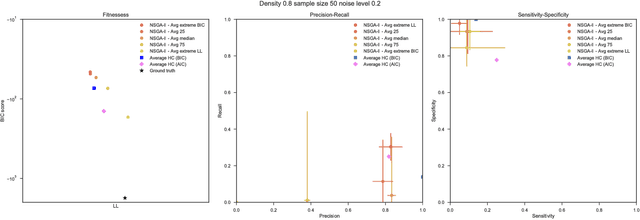
Bayesian Networks have been widely used in the last decades in many fields, to describe statistical dependencies among random variables. In general, learning the structure of such models is a problem with considerable theoretical interest that still poses many challenges. On the one hand, this is a well-known NP-complete problem, which is practically hardened by the huge search space of possible solutions. On the other hand, the phenomenon of I-equivalence, i.e., different graphical structures underpinning the same set of statistical dependencies, may lead to multimodal fitness landscapes further hindering maximum likelihood approaches to solve the task. Despite all these difficulties, greedy search methods based on a likelihood score coupled with a regularization term to account for model complexity, have been shown to be surprisingly effective in practice. In this paper, we consider the formulation of the task of learning the structure of Bayesian Networks as an optimization problem based on a likelihood score. Nevertheless, our approach do not adjust this score by means of any of the complexity terms proposed in the literature; instead, it accounts directly for the complexity of the discovered solutions by exploiting a multi-objective optimization procedure. To this extent, we adopt NSGA-II and define the first objective function to be the likelihood of a solution and the second to be the number of selected arcs. We thoroughly analyze the behavior of our method on a wide set of simulated data, and we discuss the performance considering the goodness of the inferred solutions both in terms of their objective functions and with respect to the retrieved structure. Our results show that NSGA-II can converge to solutions characterized by better likelihood and less arcs than classic approaches, although paradoxically frequently characterized by a lower similarity to the target network.

Parallel Implementation of Efficient Search Schemes for the Inference of Cancer Progression Models

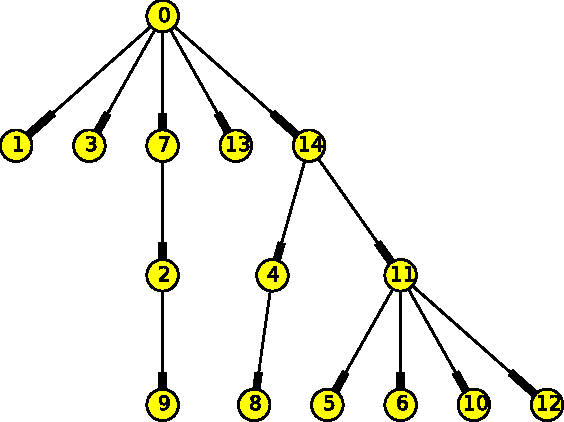
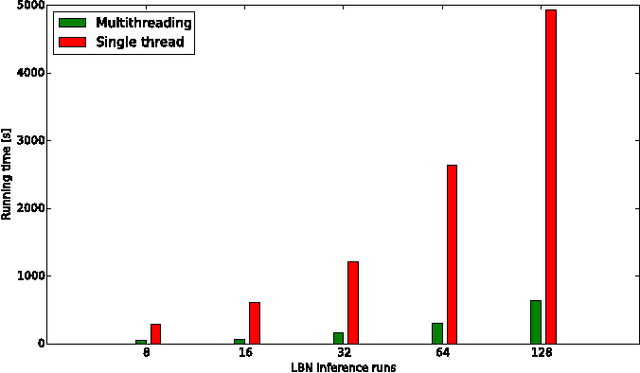
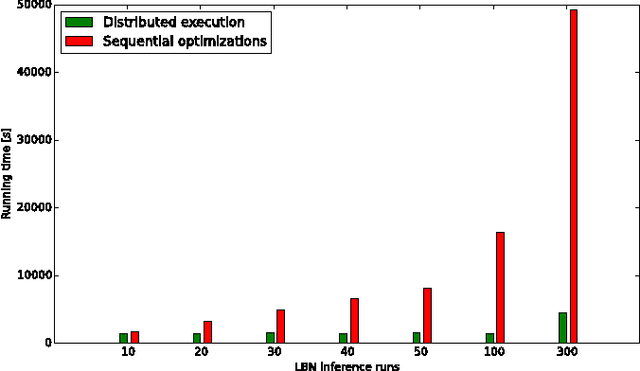
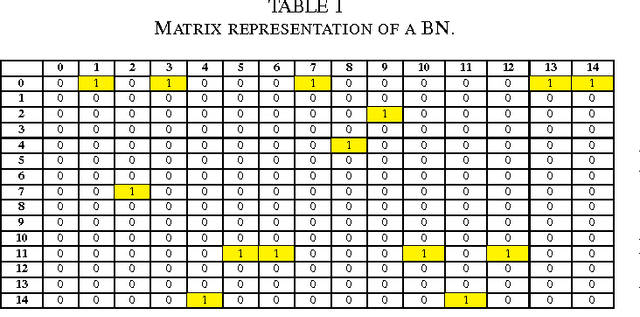
The emergence and development of cancer is a consequence of the accumulation over time of genomic mutations involving a specific set of genes, which provides the cancer clones with a functional selective advantage. In this work, we model the order of accumulation of such mutations during the progression, which eventually leads to the disease, by means of probabilistic graphic models, i.e., Bayesian Networks (BNs). We investigate how to perform the task of learning the structure of such BNs, according to experimental evidence, adopting a global optimization meta-heuristics. In particular, in this work we rely on Genetic Algorithms, and to strongly reduce the execution time of the inference -- which can also involve multiple repetitions to collect statistically significant assessments of the data -- we distribute the calculations using both multi-threading and a multi-node architecture. The results show that our approach is characterized by good accuracy and specificity; we also demonstrate its feasibility, thanks to a 84x reduction of the overall execution time with respect to a traditional sequential implementation.