Gaussian Database Alignment and Gaussian Planted Matching

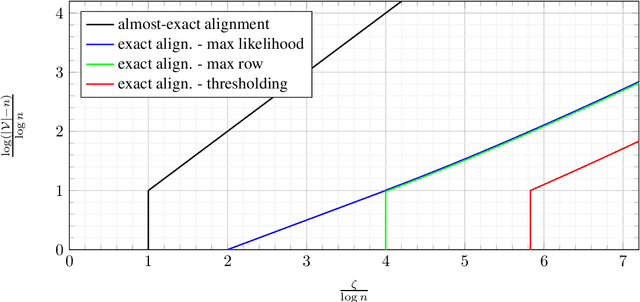
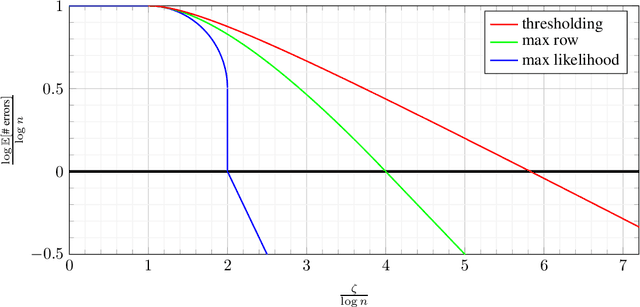
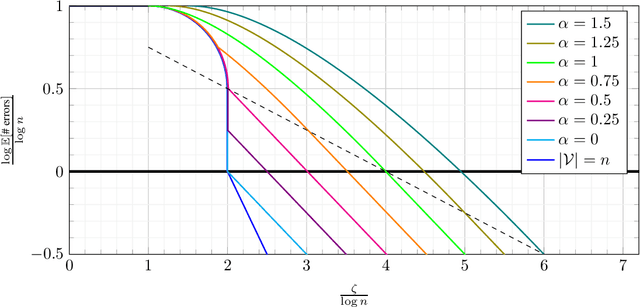
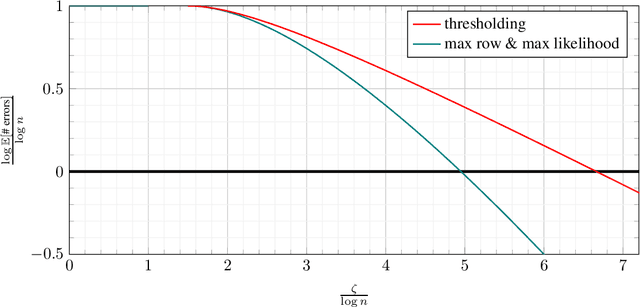
Database alignment is a variant of the graph alignment problem: Given a pair of anonymized databases containing separate yet correlated features for a set of users, the problem is to identify the correspondence between the features and align the anonymized user sets based on correlation alone. This closely relates to planted matching, where given a bigraph with random weights, the goal is to identify the underlying matching that generated the given weights. We study an instance of the database alignment problem with multivariate Gaussian features and derive results that apply both for database alignment and for planted matching, demonstrating the connection between them. The performance thresholds for database alignment converge to that for planted matching when the dimensionality of the database features is \(\omega(\log n)\), where \(n\) is the size of the alignment, and no individual feature is too strong. The maximum likelihood algorithms for both planted matching and database alignment take the form of a linear program and we study relaxations to better understand the significance of various constraints under various conditions and present achievability and converse bounds. Our results show that the almost-exact alignment threshold for the relaxed algorithms coincide with that of maximum likelihood, while there is a gap between the exact alignment thresholds. Our analysis and results extend to the unbalanced case where one user set is not fully covered by the alignment.

Characterizing the Optimal 0-1 Loss for Multi-class Classification with a Test-time Attacker

Finding classifiers robust to adversarial examples is critical for their safe deployment. Determining the robustness of the best possible classifier under a given threat model for a given data distribution and comparing it to that achieved by state-of-the-art training methods is thus an important diagnostic tool. In this paper, we find achievable information-theoretic lower bounds on loss in the presence of a test-time attacker for multi-class classifiers on any discrete dataset. We provide a general framework for finding the optimal 0-1 loss that revolves around the construction of a conflict hypergraph from the data and adversarial constraints. We further define other variants of the attacker-classifier game that determine the range of the optimal loss more efficiently than the full-fledged hypergraph construction. Our evaluation shows, for the first time, an analysis of the gap to optimal robustness for classifiers in the multi-class setting on benchmark datasets.

Lower Bounds on Cross-Entropy Loss in the Presence of Test-time Adversaries

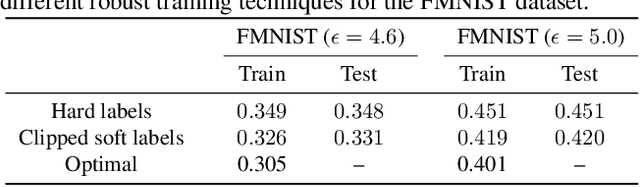
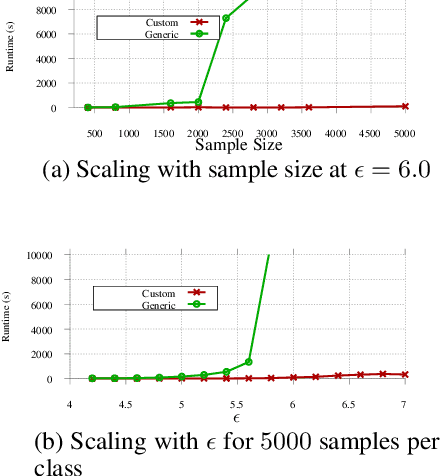
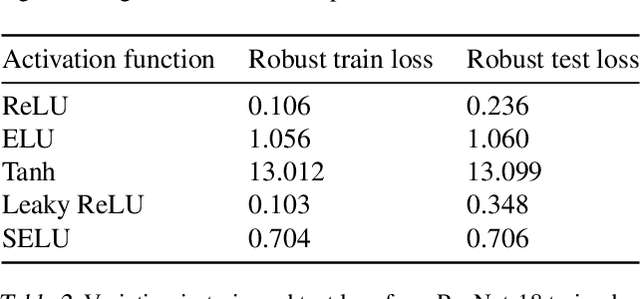
Understanding the fundamental limits of robust supervised learning has emerged as a problem of immense interest, from both practical and theoretical standpoints. In particular, it is critical to determine classifier-agnostic bounds on the training loss to establish when learning is possible. In this paper, we determine optimal lower bounds on the cross-entropy loss in the presence of test-time adversaries, along with the corresponding optimal classification outputs. Our formulation of the bound as a solution to an optimization problem is general enough to encompass any loss function depending on soft classifier outputs. We also propose and provide a proof of correctness for a bespoke algorithm to compute this lower bound efficiently, allowing us to determine lower bounds for multiple practical datasets of interest. We use our lower bounds as a diagnostic tool to determine the effectiveness of current robust training methods and find a gap from optimality at larger budgets. Finally, we investigate the possibility of using of optimal classification outputs as soft labels to empirically improve robust training.

Lower Bounds on Adversarial Robustness from Optimal Transport

While progress has been made in understanding the robustness of machine learning classifiers to test-time adversaries (evasion attacks), fundamental questions remain unresolved. In this paper, we use optimal transport to characterize the minimum possible loss in an adversarial classification scenario. In this setting, an adversary receives a random labeled example from one of two classes, perturbs the example subject to a neighborhood constraint, and presents the modified example to the classifier. We define an appropriate cost function such that the minimum transportation cost between the distributions of the two classes determines the minimum $0-1$ loss for any classifier. When the classifier comes from a restricted hypothesis class, the optimal transportation cost provides a lower bound. We apply our framework to the case of Gaussian data with norm-bounded adversaries and explicitly show matching bounds for the classification and transport problems as well as the optimality of linear classifiers. We also characterize the sample complexity of learning in this setting, deriving and extending previously known results as a special case. Finally, we use our framework to study the gap between the optimal classification performance possible and that currently achieved by state-of-the-art robustly trained neural networks for datasets of interest, namely, MNIST, Fashion MNIST and CIFAR-10.

Better the Devil you Know: An Analysis of Evasion Attacks using Out-of-Distribution Adversarial Examples

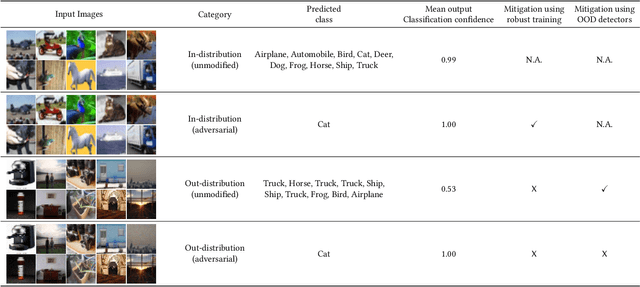
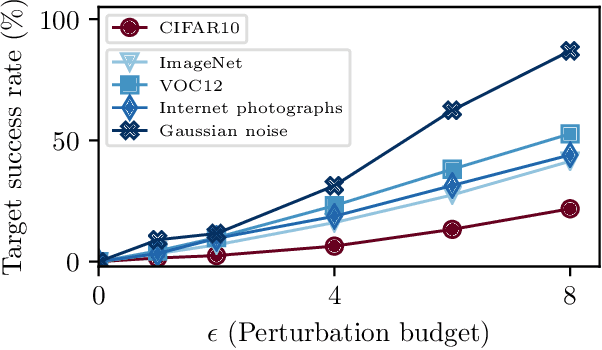
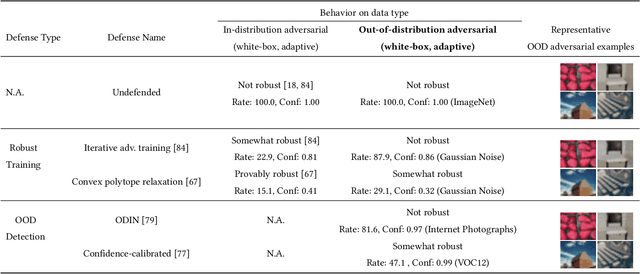
A large body of recent work has investigated the phenomenon of evasion attacks using adversarial examples for deep learning systems, where the addition of norm-bounded perturbations to the test inputs leads to incorrect output classification. Previous work has investigated this phenomenon in closed-world systems where training and test inputs follow a pre-specified distribution. However, real-world implementations of deep learning applications, such as autonomous driving and content classification are likely to operate in the open-world environment. In this paper, we demonstrate the success of open-world evasion attacks, where adversarial examples are generated from out-of-distribution inputs (OOD adversarial examples). In our study, we use 11 state-of-the-art neural network models trained on 3 image datasets of varying complexity. We first demonstrate that state-of-the-art detectors for out-of-distribution data are not robust against OOD adversarial examples. We then consider 5 known defenses for adversarial examples, including state-of-the-art robust training methods, and show that against these defenses, OOD adversarial examples can achieve up to 4$\times$ higher target success rates compared to adversarial examples generated from in-distribution data. We also take a quantitative look at how open-world evasion attacks may affect real-world systems. Finally, we present the first steps towards a robust open-world machine learning system.

Database Alignment with Gaussian Features

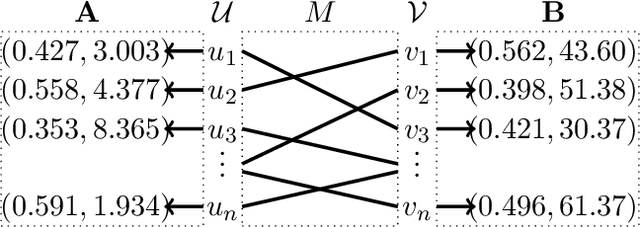
We consider the problem of aligning a pair of databases with jointly Gaussian features. We consider two algorithms, complete database alignment via MAP estimation among all possible database alignments, and partial alignment via a thresholding approach of log likelihood ratios. We derive conditions on mutual information between feature pairs, identifying the regimes where the algorithms are guaranteed to perform reliably and those where they cannot be expected to succeed.

Partial Recovery of Erdős-Rényi Graph Alignment via $k$-Core Alignment

We determine information theoretic conditions under which it is possible to partially recover the alignment used to generate a pair of sparse, correlated Erd\H{o}s-R\'enyi graphs. To prove our achievability result, we introduce the $k$-core alignment estimator. This estimator searches for an alignment in which the intersection of the correlated graphs using this alignment has a minimum degree of $k$. We prove a matching converse bound. As the number of vertices grows, recovery of the alignment for a fraction of the vertices tending to one is possible when the average degree of the intersection of the graph pair tends to infinity. It was previously known that exact alignment is possible when this average degree grows faster than the logarithm of the number of vertices.

PAC-learning in the presence of evasion adversaries

The existence of evasion attacks during the test phase of machine learning algorithms represents a significant challenge to both their deployment and understanding. These attacks can be carried out by adding imperceptible perturbations to inputs to generate adversarial examples and finding effective defenses and detectors has proven to be difficult. In this paper, we step away from the attack-defense arms race and seek to understand the limits of what can be learned in the presence of an evasion adversary. In particular, we extend the Probably Approximately Correct (PAC)-learning framework to account for the presence of an adversary. We first define corrupted hypothesis classes which arise from standard binary hypothesis classes in the presence of an evasion adversary and derive the Vapnik-Chervonenkis (VC)-dimension for these, denoted as the adversarial VC-dimension. We then show that sample complexity upper bounds from the Fundamental Theorem of Statistical learning can be extended to the case of evasion adversaries, where the sample complexity is controlled by the adversarial VC-dimension. We then explicitly derive the adversarial VC-dimension for halfspace classifiers in the presence of a sample-wise norm-constrained adversary of the type commonly studied for evasion attacks and show that it is the same as the standard VC-dimension, closing an open question. Finally, we prove that the adversarial VC-dimension can be either larger or smaller than the standard VC-dimension depending on the hypothesis class and adversary, making it an interesting object of study in its own right.

Exact alignment recovery for correlated Erdős-Rényi graphs

We consider the problem of perfectly recovering the vertex correspondence between two correlated Erd\H{o}s-R\'enyi (ER) graphs on the same vertex set. The correspondence between the vertices can be obscured by randomly permuting the vertex labels of one of the graphs. We determine the information-theoretic threshold for exact recovery, i.e. the conditions under which the entire vertex correspondence can be correctly recovered given unbounded computational resources.

On the Performance of a Canonical Labeling for Matching Correlated Erdős-Rényi Graphs

Graph matching in two correlated random graphs refers to the task of identifying the correspondence between vertex sets of the graphs. Recent results have characterized the exact information-theoretic threshold for graph matching in correlated Erd\H{o}s-R\'enyi graphs. However, very little is known about the existence of efficient algorithms to achieve graph matching without seeds. In this work we identify a region in which a straightforward $O(n^2\log n)$-time canonical labeling algorithm, initially introduced in the context of graph isomorphism, succeeds in matching correlated Erd\H{o}s-R\'enyi graphs. The algorithm has two steps. In the first step, all vertices are labeled by their degrees and a trivial minimum distance matching (i.e., simply sorting vertices according to their degrees) matches a fixed number of highest degree vertices in the two graphs. Having identified this subset of vertices, the remaining vertices are matched using a matching algorithm for bipartite graphs.