On the Performance of a Canonical Labeling for Matching Correlated Erdős-Rényi Graphs
Paper and Code
Apr 25, 2018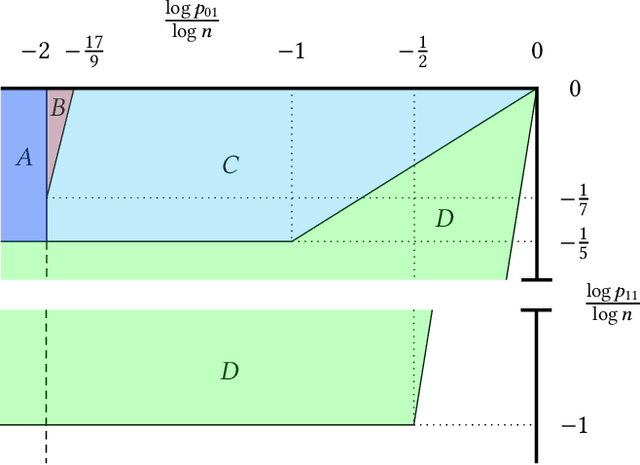
Graph matching in two correlated random graphs refers to the task of identifying the correspondence between vertex sets of the graphs. Recent results have characterized the exact information-theoretic threshold for graph matching in correlated Erd\H{o}s-R\'enyi graphs. However, very little is known about the existence of efficient algorithms to achieve graph matching without seeds. In this work we identify a region in which a straightforward $O(n^2\log n)$-time canonical labeling algorithm, initially introduced in the context of graph isomorphism, succeeds in matching correlated Erd\H{o}s-R\'enyi graphs. The algorithm has two steps. In the first step, all vertices are labeled by their degrees and a trivial minimum distance matching (i.e., simply sorting vertices according to their degrees) matches a fixed number of highest degree vertices in the two graphs. Having identified this subset of vertices, the remaining vertices are matched using a matching algorithm for bipartite graphs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge