Gaussian Database Alignment and Gaussian Planted Matching

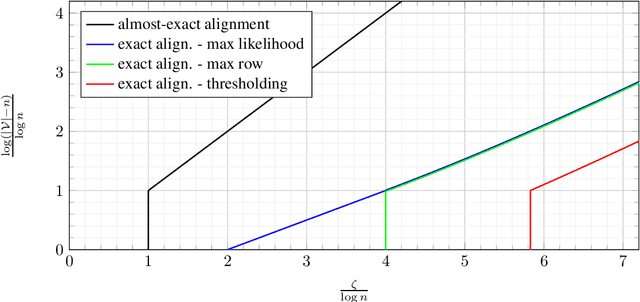
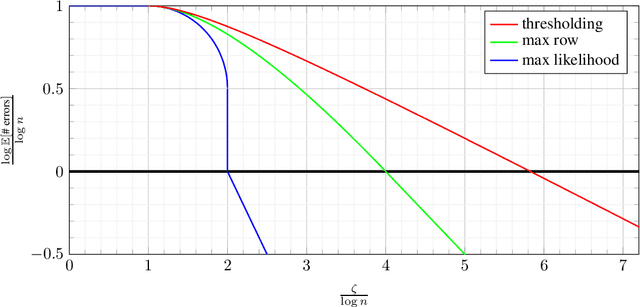
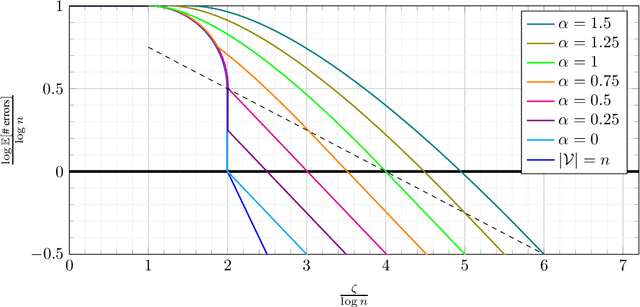
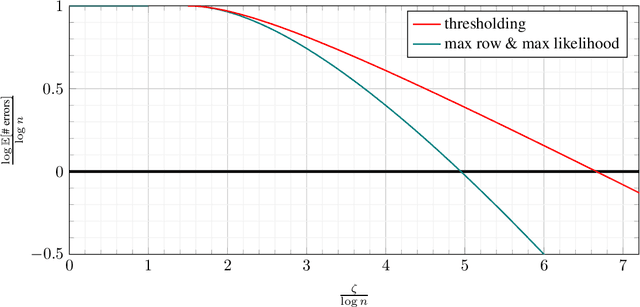
Database alignment is a variant of the graph alignment problem: Given a pair of anonymized databases containing separate yet correlated features for a set of users, the problem is to identify the correspondence between the features and align the anonymized user sets based on correlation alone. This closely relates to planted matching, where given a bigraph with random weights, the goal is to identify the underlying matching that generated the given weights. We study an instance of the database alignment problem with multivariate Gaussian features and derive results that apply both for database alignment and for planted matching, demonstrating the connection between them. The performance thresholds for database alignment converge to that for planted matching when the dimensionality of the database features is \(\omega(\log n)\), where \(n\) is the size of the alignment, and no individual feature is too strong. The maximum likelihood algorithms for both planted matching and database alignment take the form of a linear program and we study relaxations to better understand the significance of various constraints under various conditions and present achievability and converse bounds. Our results show that the almost-exact alignment threshold for the relaxed algorithms coincide with that of maximum likelihood, while there is a gap between the exact alignment thresholds. Our analysis and results extend to the unbalanced case where one user set is not fully covered by the alignment.

Database Alignment with Gaussian Features

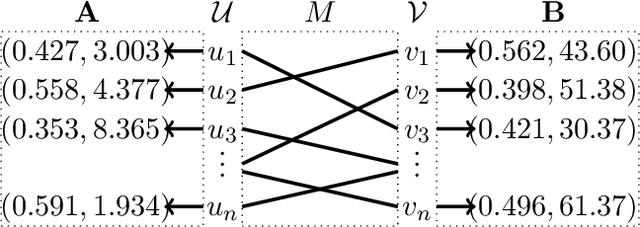
We consider the problem of aligning a pair of databases with jointly Gaussian features. We consider two algorithms, complete database alignment via MAP estimation among all possible database alignments, and partial alignment via a thresholding approach of log likelihood ratios. We derive conditions on mutual information between feature pairs, identifying the regimes where the algorithms are guaranteed to perform reliably and those where they cannot be expected to succeed.

On the Performance of a Canonical Labeling for Matching Correlated Erdős-Rényi Graphs

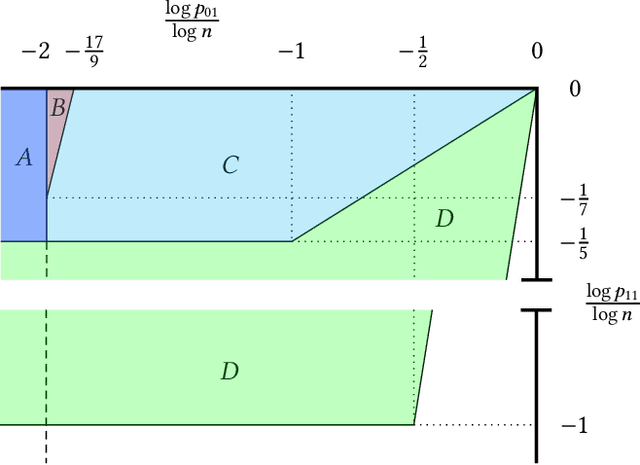
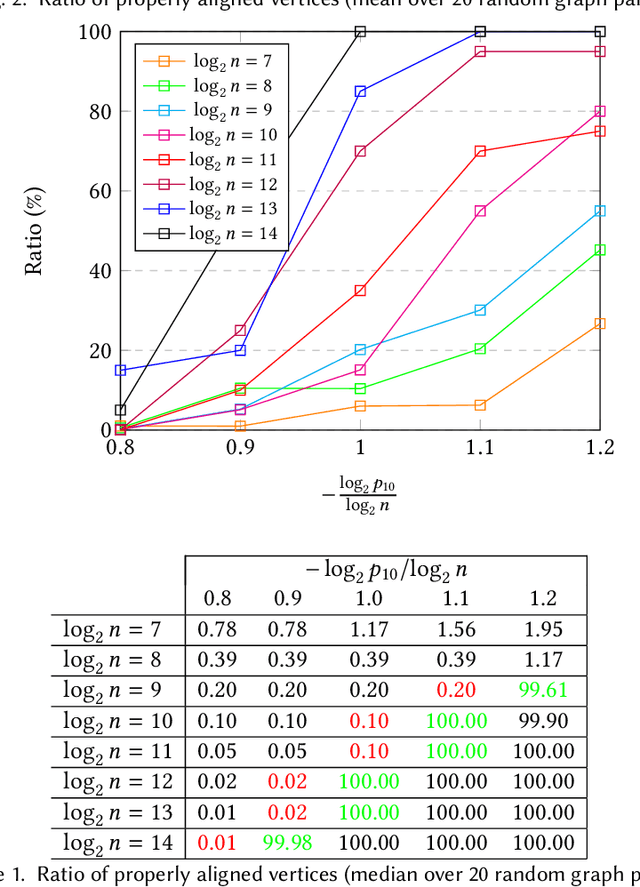
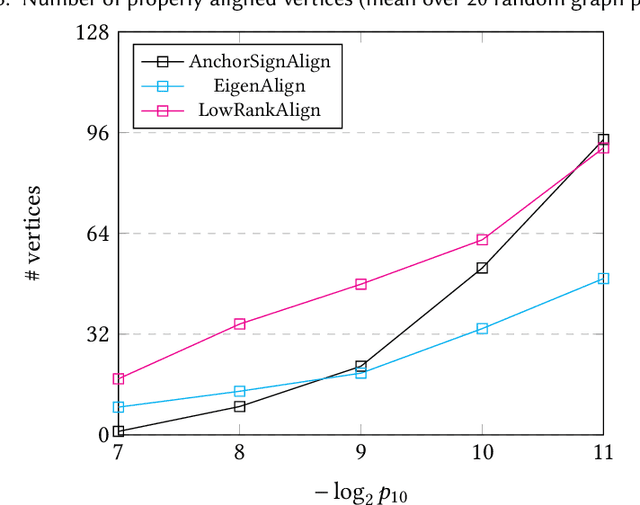
Graph matching in two correlated random graphs refers to the task of identifying the correspondence between vertex sets of the graphs. Recent results have characterized the exact information-theoretic threshold for graph matching in correlated Erd\H{o}s-R\'enyi graphs. However, very little is known about the existence of efficient algorithms to achieve graph matching without seeds. In this work we identify a region in which a straightforward $O(n^2\log n)$-time canonical labeling algorithm, initially introduced in the context of graph isomorphism, succeeds in matching correlated Erd\H{o}s-R\'enyi graphs. The algorithm has two steps. In the first step, all vertices are labeled by their degrees and a trivial minimum distance matching (i.e., simply sorting vertices according to their degrees) matches a fixed number of highest degree vertices in the two graphs. Having identified this subset of vertices, the remaining vertices are matched using a matching algorithm for bipartite graphs.