Lower Bounds on Cross-Entropy Loss in the Presence of Test-time Adversaries
Paper and Code
Apr 16, 2021
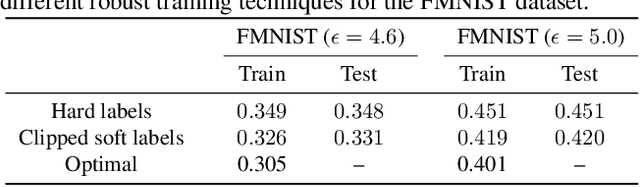
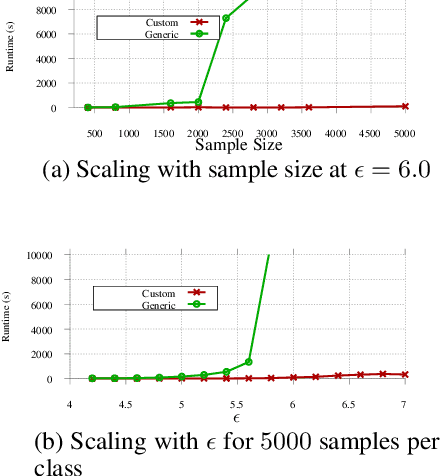
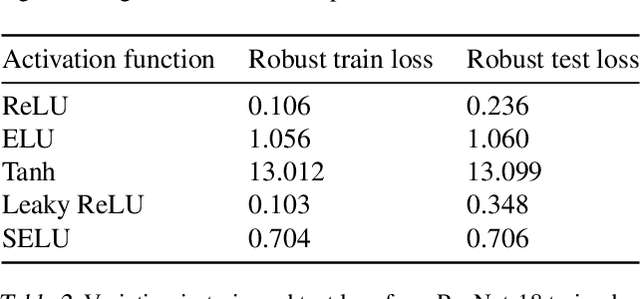
Understanding the fundamental limits of robust supervised learning has emerged as a problem of immense interest, from both practical and theoretical standpoints. In particular, it is critical to determine classifier-agnostic bounds on the training loss to establish when learning is possible. In this paper, we determine optimal lower bounds on the cross-entropy loss in the presence of test-time adversaries, along with the corresponding optimal classification outputs. Our formulation of the bound as a solution to an optimization problem is general enough to encompass any loss function depending on soft classifier outputs. We also propose and provide a proof of correctness for a bespoke algorithm to compute this lower bound efficiently, allowing us to determine lower bounds for multiple practical datasets of interest. We use our lower bounds as a diagnostic tool to determine the effectiveness of current robust training methods and find a gap from optimality at larger budgets. Finally, we investigate the possibility of using of optimal classification outputs as soft labels to empirically improve robust training.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge