Unsupervised Congestion Status Identification Using LMP Data

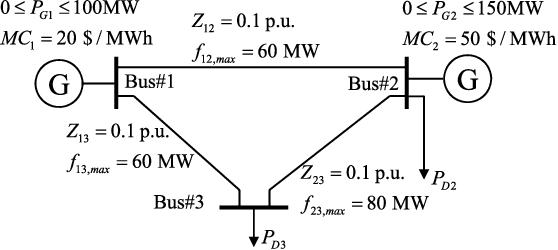
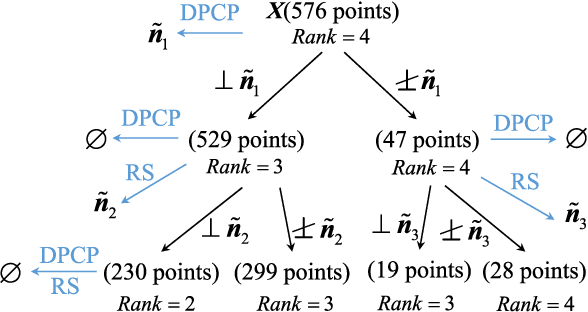
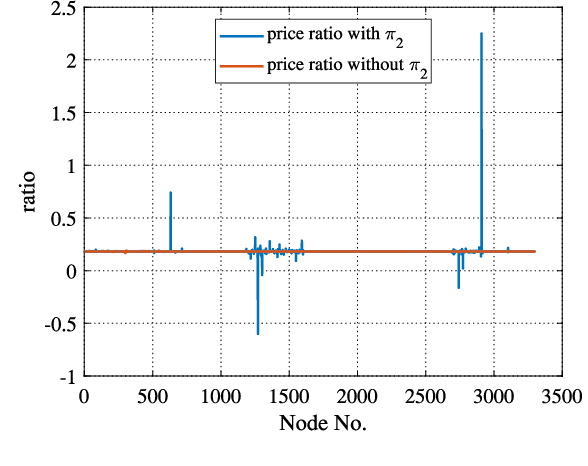
Having a better understanding of how locational marginal prices (LMPs) change helps in price forecasting and market strategy making. This paper investigates the fundamental distribution of the congestion part of LMPs in high-dimensional Euclidean space using an unsupervised approach. LMP models based on the lossless and lossy DC optimal power flow (DC-OPF) are analyzed to show the overlapping subspace property of the LMP data. The congestion part of LMPs is spanned by certain row vectors of the power transfer distribution factor (PTDF) matrix, and the subspace attributes of an LMP vector uniquely are found to reflect the instantaneous congestion status of all the transmission lines. The proposed method searches for the basis vectors that span the subspaces of congestion LMP data in hierarchical ways. In the bottom-up search, the data belonging to 1-dimensional subspaces are detected, and other data are projected on the orthogonal subspaces. This procedure is repeated until all the basis vectors are found or the basis gap appears. Top-down searching is used to address the basis gap by hyperplane detection with outliers. Once all the basis vectors are detected, the congestion status can be identified. Numerical experiments based on the IEEE 30-bus system, IEEE 118-bus system, Illinois 200-bus system, and Southwest Power Pool are conducted to show the performance of the proposed method.

A Novel Combined Data-Driven Approach for Electricity Theft Detection

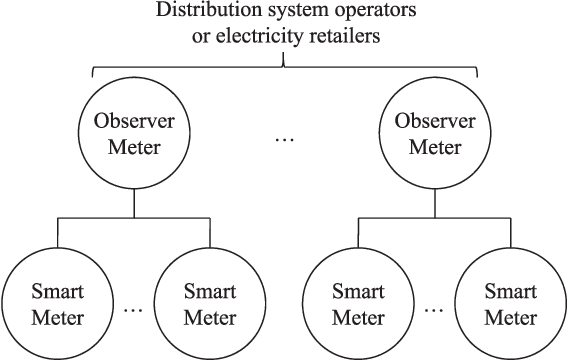
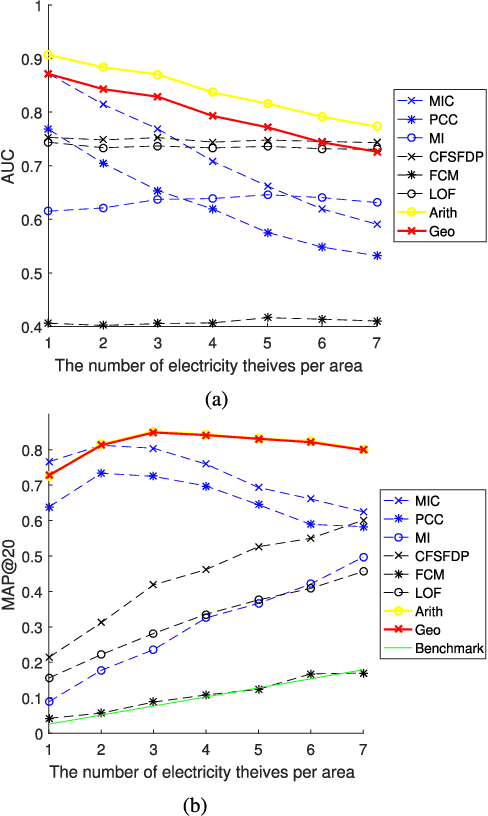
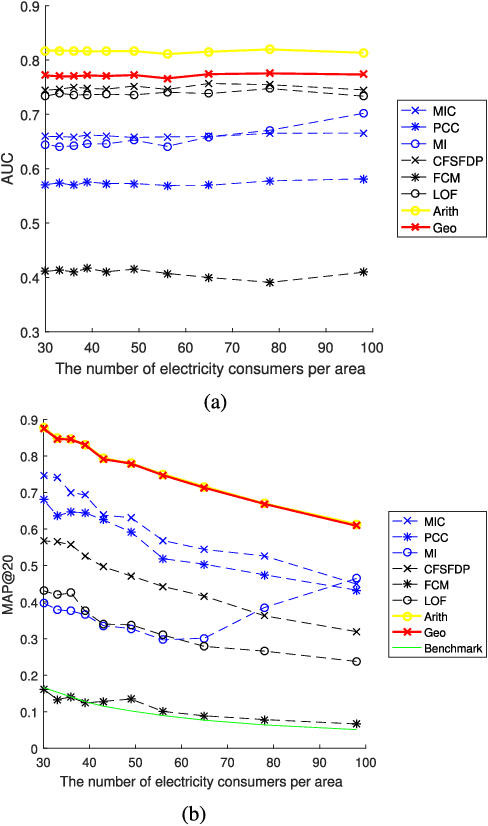
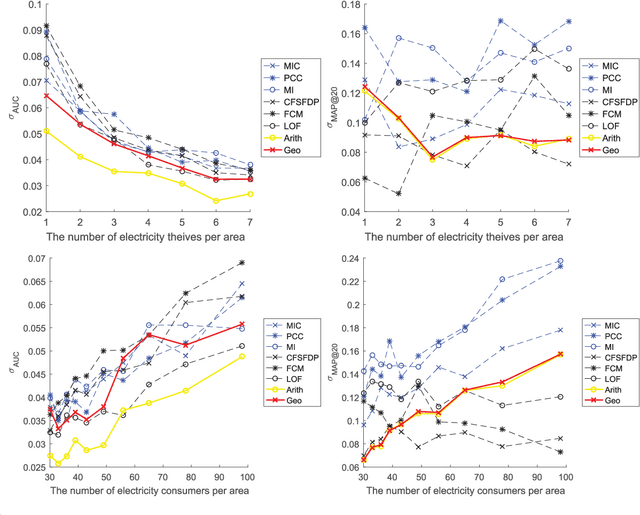
The two-way flow of information and energy is an important feature of the Energy Internet. Data analytics is a powerful tool in the information flow that aims to solve practical problems using data mining techniques. As the problem of electricity thefts via tampering with smart meters continues to increase, the abnormal behaviors of thefts become more diversified and more difficult to detect. Thus, a data analytics method for detecting various types of electricity thefts is required. However, the existing methods either require a labeled dataset or additional system information which is difficult to obtain in reality or have poor detection accuracy. In this paper, we combine two novel data mining techniques to solve the problem. One technique is the Maximum Information Coefficient (MIC), which can find the correlations between the non-technical loss (NTL) and a certain electricity behavior of the consumer. MIC can be used to precisely detect thefts that appear normal in shapes. The other technique is the clustering technique by fast search and find of density peaks (CFSFDP). CFSFDP finds the abnormal users among thousands of load profiles, making it quite suitable for detecting electricity thefts with arbitrary shapes. Next, a framework for combining the advantages of the two techniques is proposed. Numerical experiments on the Irish smart meter dataset are conducted to show the good performance of the combined method.

Real-time scheduling of renewable power systems through planning-based reinforcement learning

The growing renewable energy sources have posed significant challenges to traditional power scheduling. It is difficult for operators to obtain accurate day-ahead forecasts of renewable generation, thereby requiring the future scheduling system to make real-time scheduling decisions aligning with ultra-short-term forecasts. Restricted by the computation speed, traditional optimization-based methods can not solve this problem. Recent developments in reinforcement learning (RL) have demonstrated the potential to solve this challenge. However, the existing RL methods are inadequate in terms of constraint complexity, algorithm performance, and environment fidelity. We are the first to propose a systematic solution based on the state-of-the-art reinforcement learning algorithm and the real power grid environment. The proposed approach enables planning and finer time resolution adjustments of power generators, including unit commitment and economic dispatch, thus increasing the grid's ability to admit more renewable energy. The well-trained scheduling agent significantly reduces renewable curtailment and load shedding, which are issues arising from traditional scheduling's reliance on inaccurate day-ahead forecasts. High-frequency control decisions exploit the existing units' flexibility, reducing the power grid's dependence on hardware transformations and saving investment and operating costs, as demonstrated in experimental results. This research exhibits the potential of reinforcement learning in promoting low-carbon and intelligent power systems and represents a solid step toward sustainable electricity generation.

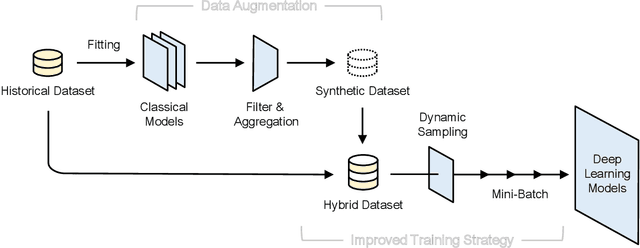
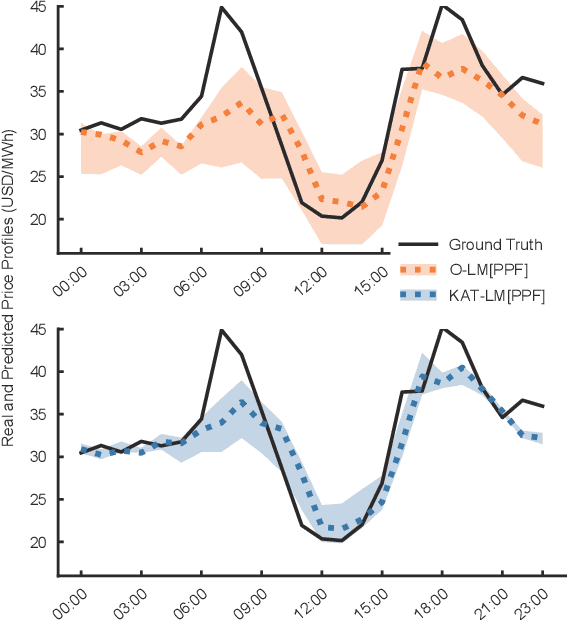
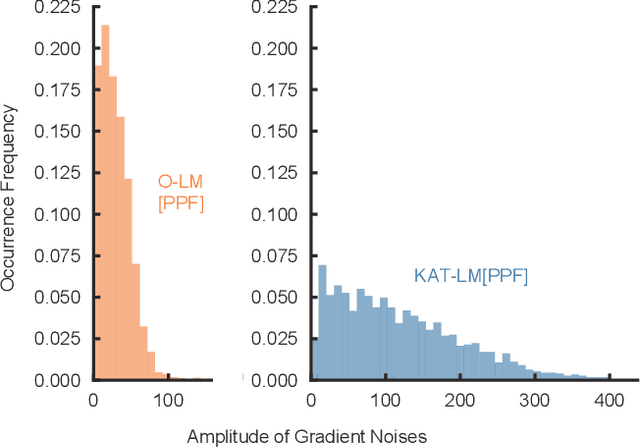
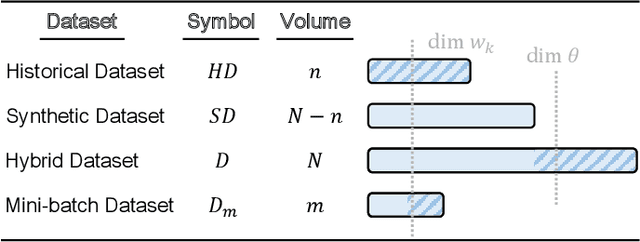
Improving Sample Efficiency of Deep Learning Models in Electricity Market

The superior performance of deep learning relies heavily on a large collection of sample data, but the data insufficiency problem turns out to be relatively common in global electricity markets. How to prevent overfitting in this case becomes a fundamental challenge when training deep learning models in different market applications. With this in mind, we propose a general framework, namely Knowledge-Augmented Training (KAT), to improve the sample efficiency, and the main idea is to incorporate domain knowledge into the training procedures of deep learning models. Specifically, we propose a novel data augmentation technique to generate some synthetic data, which are later processed by an improved training strategy. This KAT methodology follows and realizes the idea of combining analytical and deep learning models together. Modern learning theories demonstrate the effectiveness of our method in terms of effective prediction error feedbacks, a reliable loss function, and rich gradient noises. At last, we study two popular applications in detail: user modeling and probabilistic price forecasting. The proposed method outperforms other competitors in all numerical tests, and the underlying reasons are explained by further statistical and visualization results.

Estimating Demand Flexibility Using Siamese LSTM Neural Networks

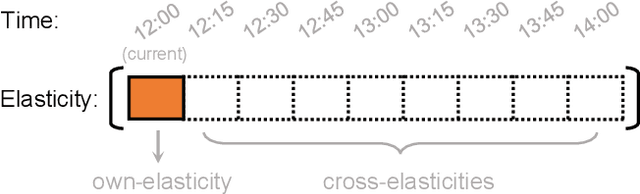
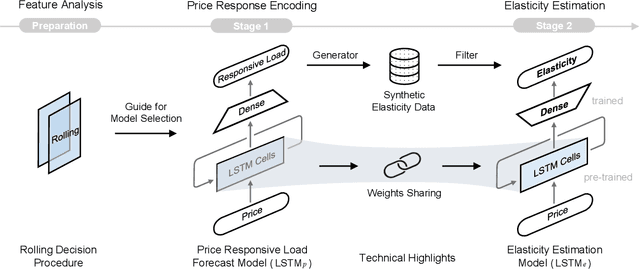
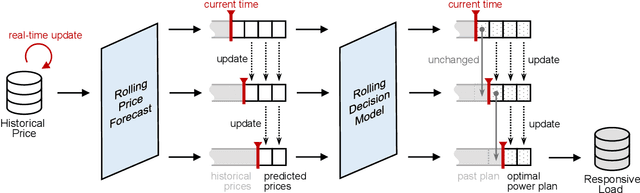
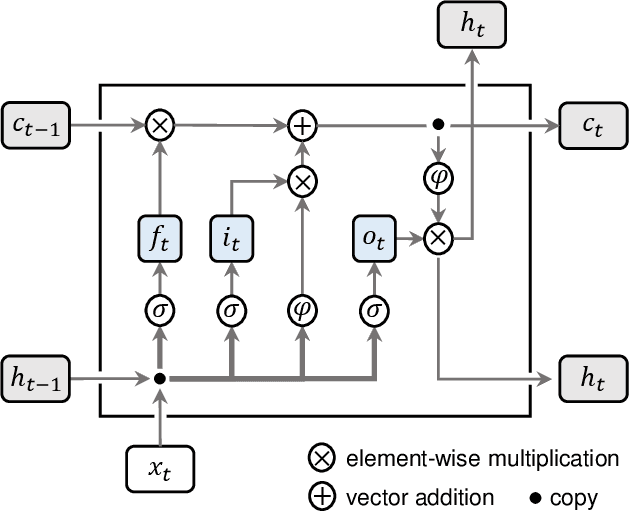
There is an opportunity in modern power systems to explore the demand flexibility by incentivizing consumers with dynamic prices. In this paper, we quantify demand flexibility using an efficient tool called time-varying elasticity, whose value may change depending on the prices and decision dynamics. This tool is particularly useful for evaluating the demand response potential and system reliability. Recent empirical evidences have highlighted some abnormal features when studying demand flexibility, such as delayed responses and vanishing elasticities after price spikes. Existing methods fail to capture these complicated features because they heavily rely on some predefined (often over-simplified) regression expressions. Instead, this paper proposes a model-free methodology to automatically and accurately derive the optimal estimation pattern. We further develop a two-stage estimation process with Siamese long short-term memory (LSTM) networks. Here, a LSTM network encodes the price response, while the other network estimates the time-varying elasticities. In the case study, the proposed framework and models are validated to achieve higher overall estimation accuracy and better description for various abnormal features when compared with the state-of-the-art methods.

Sparse Oblique Decision Tree for Power System Security Rules Extraction and Embedding

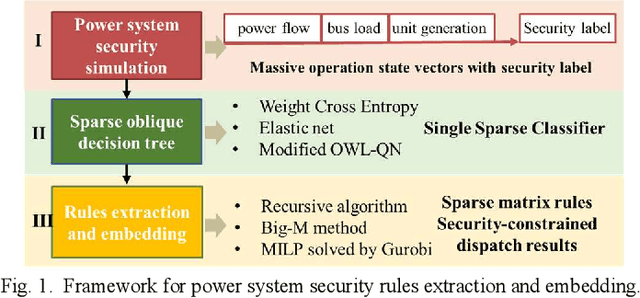
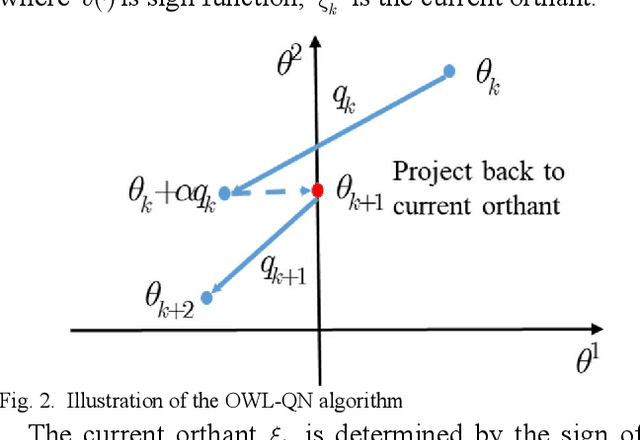
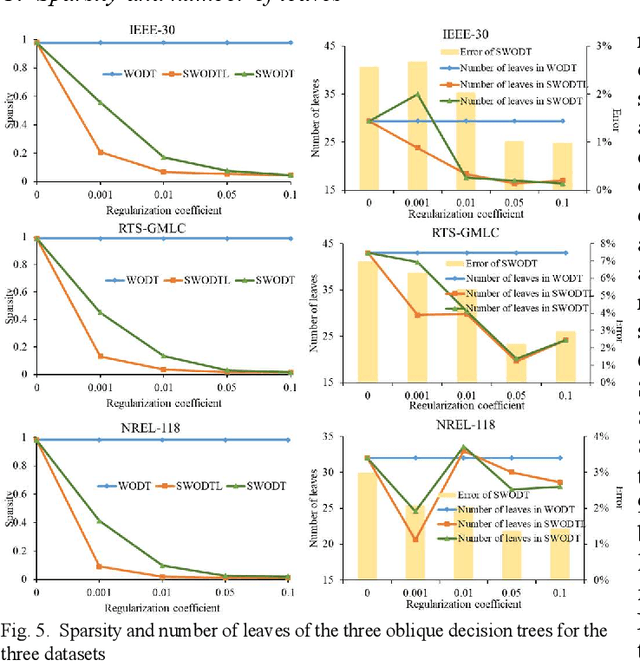
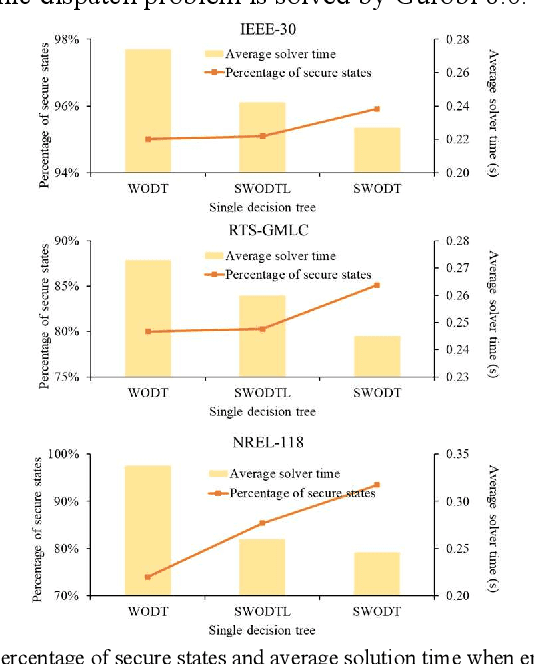
Increasing the penetration of variable generation has a substantial effect on the operational reliability of power systems. The higher level of uncertainty that stems from this variability makes it more difficult to determine whether a given operating condition will be secure or insecure. Data-driven techniques provide a promising way to identify security rules that can be embedded in economic dispatch model to keep power system operating states secure. This paper proposes using a sparse weighted oblique decision tree to learn accurate, understandable, and embeddable security rules that are linear and can be extracted as sparse matrices using a recursive algorithm. These matrices can then be easily embedded as security constraints in power system economic dispatch calculations using the Big-M method. Tests on several large datasets with high renewable energy penetration demonstrate the effectiveness of the proposed method. In particular, the sparse weighted oblique decision tree outperforms the state-of-art weighted oblique decision tree while keeping the security rules simple. When embedded in the economic dispatch, these rules significantly increase the percentage of secure states and reduce the average solution time.

Bounding Data-driven Model Errors in Power Grid Analysis

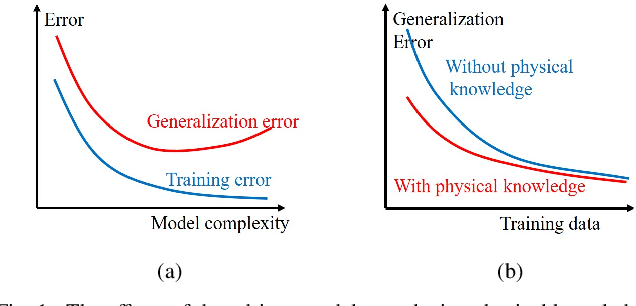
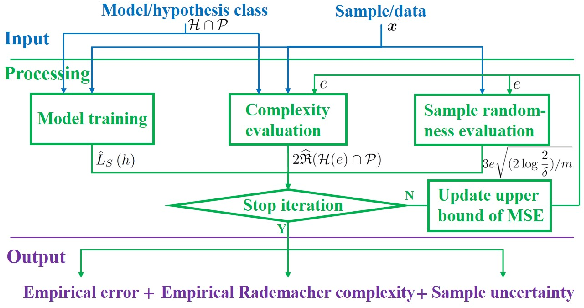
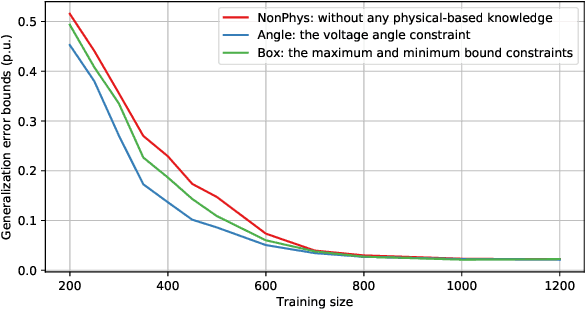
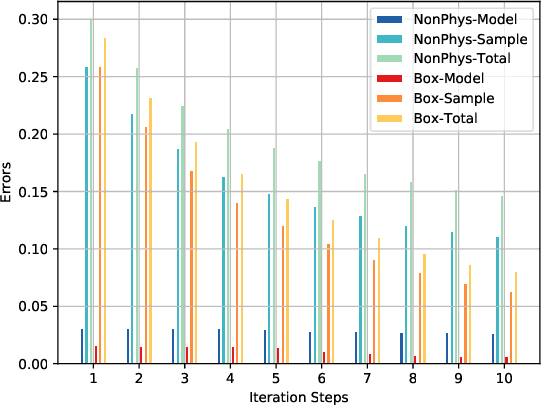
Data-driven models analyze power grids under incomplete physical information, and their accuracy has been mostly validated empirically using certain training and testing datasets. This paper explores error bounds for data-driven models under all possible training and testing scenarios, and proposes an evaluation implementation based on Rademacher complexity theory. We answer key questions for data-driven models: how much training data is required to guarantee a certain error bound, and how partial physical knowledge can be utilized to reduce the required amount of data. Our results are crucial for the evaluation and application of data-driven models in power grid analysis. We demonstrate the proposed method by finding generalization error bounds for two applications, i.e. branch flow linearization and external network equivalent under different degrees of physical knowledge. Results identify how the bounds decrease with additional power grid physical knowledge or more training data.