Differentially Private Algorithms for Synthetic Power System Datasets

While power systems research relies on the availability of real-world network datasets, data owners (e.g., system operators) are hesitant to share data due to security and privacy risks. To control these risks, we develop privacy-preserving algorithms for the synthetic generation of optimization and machine learning datasets. Taking a real-world dataset as input, the algorithms output its noisy, synthetic version, which preserves the accuracy of the real data on a specific downstream model or even a large population of those. We control the privacy loss using Laplace and Exponential mechanisms of differential privacy and preserve data accuracy using a post-processing convex optimization. We apply the algorithms to generate synthetic network parameters and wind power data.

Bounding Data-driven Model Errors in Power Grid Analysis

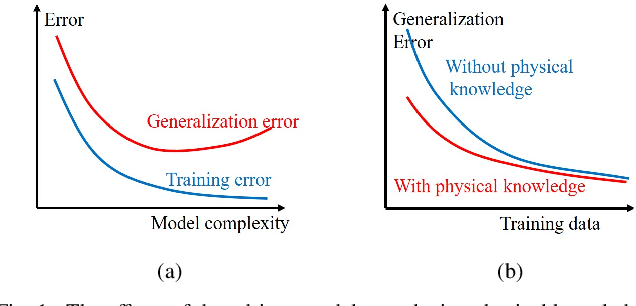
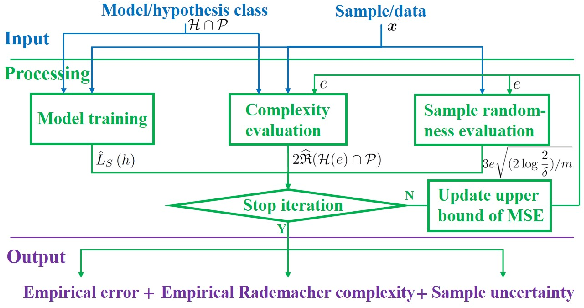
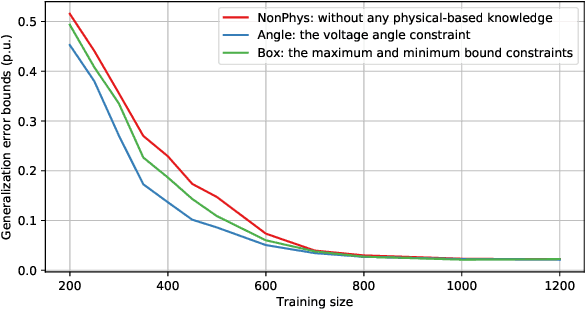
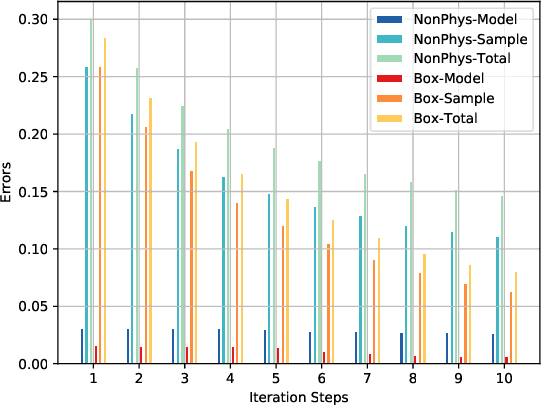
Data-driven models analyze power grids under incomplete physical information, and their accuracy has been mostly validated empirically using certain training and testing datasets. This paper explores error bounds for data-driven models under all possible training and testing scenarios, and proposes an evaluation implementation based on Rademacher complexity theory. We answer key questions for data-driven models: how much training data is required to guarantee a certain error bound, and how partial physical knowledge can be utilized to reduce the required amount of data. Our results are crucial for the evaluation and application of data-driven models in power grid analysis. We demonstrate the proposed method by finding generalization error bounds for two applications, i.e. branch flow linearization and external network equivalent under different degrees of physical knowledge. Results identify how the bounds decrease with additional power grid physical knowledge or more training data.