Unsupervised Congestion Status Identification Using LMP Data
Paper and Code
Nov 15, 2024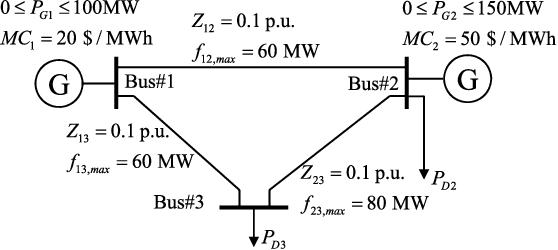
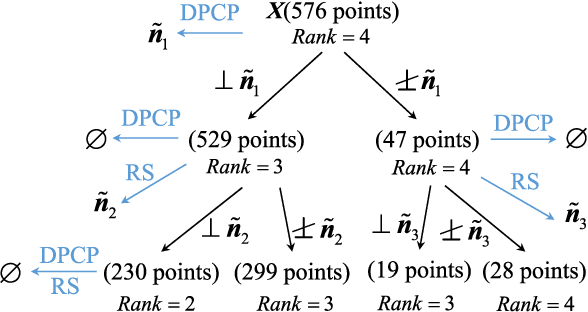
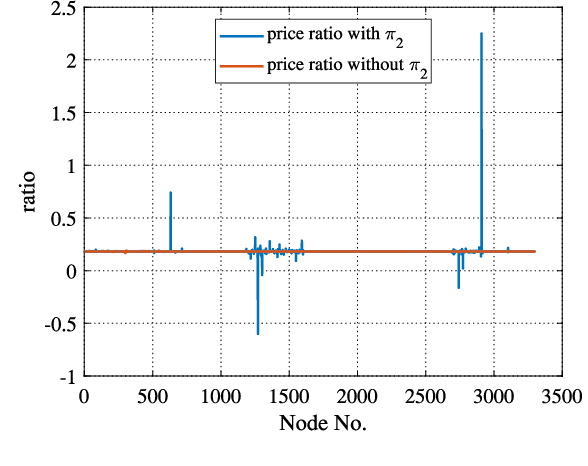

Having a better understanding of how locational marginal prices (LMPs) change helps in price forecasting and market strategy making. This paper investigates the fundamental distribution of the congestion part of LMPs in high-dimensional Euclidean space using an unsupervised approach. LMP models based on the lossless and lossy DC optimal power flow (DC-OPF) are analyzed to show the overlapping subspace property of the LMP data. The congestion part of LMPs is spanned by certain row vectors of the power transfer distribution factor (PTDF) matrix, and the subspace attributes of an LMP vector uniquely are found to reflect the instantaneous congestion status of all the transmission lines. The proposed method searches for the basis vectors that span the subspaces of congestion LMP data in hierarchical ways. In the bottom-up search, the data belonging to 1-dimensional subspaces are detected, and other data are projected on the orthogonal subspaces. This procedure is repeated until all the basis vectors are found or the basis gap appears. Top-down searching is used to address the basis gap by hyperplane detection with outliers. Once all the basis vectors are detected, the congestion status can be identified. Numerical experiments based on the IEEE 30-bus system, IEEE 118-bus system, Illinois 200-bus system, and Southwest Power Pool are conducted to show the performance of the proposed method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge